正弦定理
图片预览







文档简介
(共26张PPT)
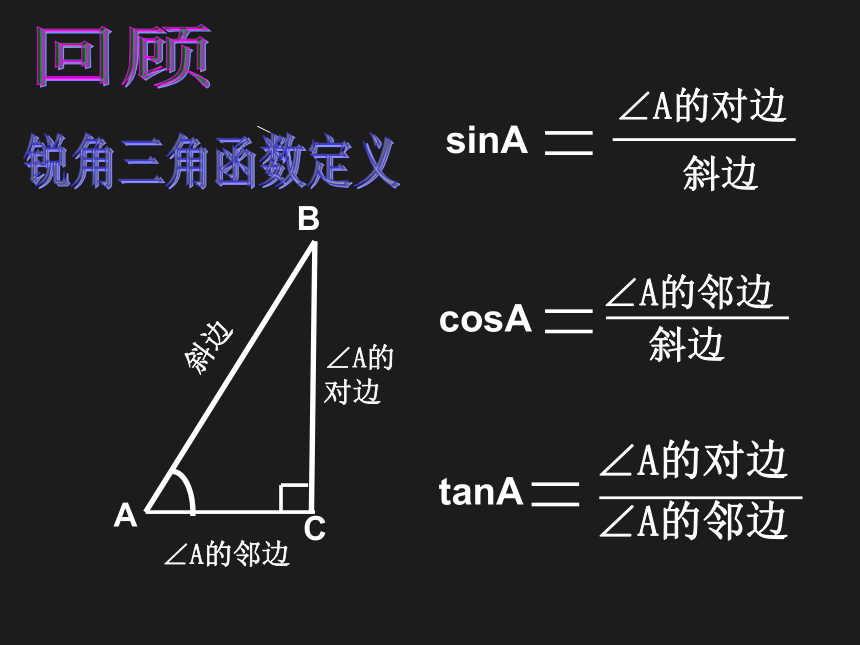
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
斜边
∠A的对边
sinA
斜边
A
B
C
∠A的对边
∠A的邻边
斜边
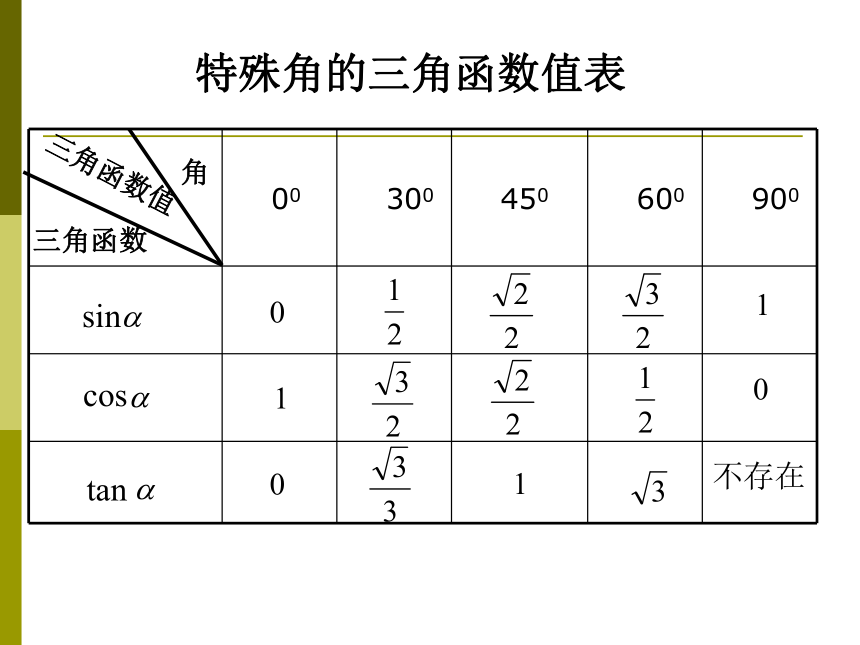
特殊角的三角函数值表
00 300 450 600 900
三角函数
三角函数值
角
sin
cos
tan
思考:在三角形ABC中,
(1)若cosA= ,求角A.
(2)若sinA= ,求角A
(3)sin75°=? sin105°=?
两角和与差的正弦
两角和与差的正切
两角和与差的余弦
sin( + )=sin cos +cos sin
sin( )=sin cos cos sin
二倍角公式及其变形
正 弦 定 理
提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
即:
A
C
B
b
a
c
以上关系式能否推广到斜三角形?
新知讲授
O
B/
c
b
a
C
B
A
R
C
c
R
c
B
C
B
C
BAB
2
sin
2
sin
sin
,
90
'
'
'
=
\
=
=
\
=
°
=
Q
B`
A
B
C
b
O
A
B
C
b
O
B`
A
B
C
b
O
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;
注 意:
定理的应用
例 1
在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b (精确到0.01).
解:
且
∵
∴
b =
19.32
=
已知两角和任意边,
求其他两边和一角
∵
∴
a =
14.14
=
B
A
C
b
c
a
剖析定理、加深理解
正弦定理可以解决三角形中哪类问题:
①
已知两角和一边,求其他角和边.
②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.
正弦定理
在 中,已知 ,求 .
典型例题
解:由
得
∵ 在 中
∴ A 为锐角
1.已知△ABC中,A:B:C=1:2:3,求a:b:c
练习
答案:1: :2
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
斜边
∠A的对边
sinA
斜边
A
B
C
∠A的对边
∠A的邻边
斜边
特殊角的三角函数值表
00 300 450 600 900
三角函数
三角函数值
角
sin
cos
tan
思考:在三角形ABC中,
(1)若cosA= ,求角A.
(2)若sinA= ,求角A
(3)sin75°=? sin105°=?
两角和与差的正弦
两角和与差的正切
两角和与差的余弦
sin( + )=sin cos +cos sin
sin( )=sin cos cos sin
二倍角公式及其变形
正 弦 定 理
提出问题,猜想命题:
在直角三角形ABC中找出a, b, c与sinA, sinB, sinC之间的关系:
A
C
B
b
a
c
即:
A
C
B
b
a
c
以上关系式能否推广到斜三角形?
新知讲授
O
B/
c
b
a
C
B
A
R
C
c
R
c
B
C
B
C
BAB
2
sin
2
sin
sin
,
90
'
'
'
=
\
=
=
\
=
°
=
Q
B`
A
B
C
b
O
A
B
C
b
O
B`
A
B
C
b
O
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;
注 意:
定理的应用
例 1
在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b (精确到0.01).
解:
且
∵
∴
b =
19.32
=
已知两角和任意边,
求其他两边和一角
∵
∴
a =
14.14
=
B
A
C
b
c
a
剖析定理、加深理解
正弦定理可以解决三角形中哪类问题:
①
已知两角和一边,求其他角和边.
②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.
正弦定理
在 中,已知 ,求 .
典型例题
解:由
得
∵ 在 中
∴ A 为锐角
1.已知△ABC中,A:B:C=1:2:3,求a:b:c
练习
答案:1: :2
