余弦定理
图片预览





文档简介
(共26张PPT)
千岛湖
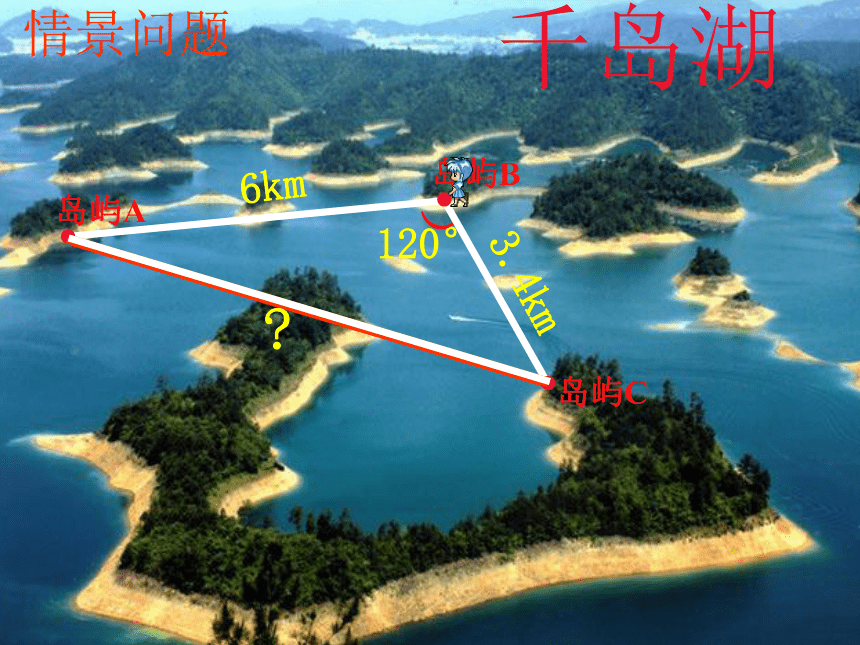
3.4km
6km
120°
)
情景问题
岛屿B
岛屿A
岛屿C
千岛湖
千岛湖
情景问题
3.4km
6km
120°
)
岛屿B
岛屿A
岛屿C
3.4km
6km
120°
A
B
C
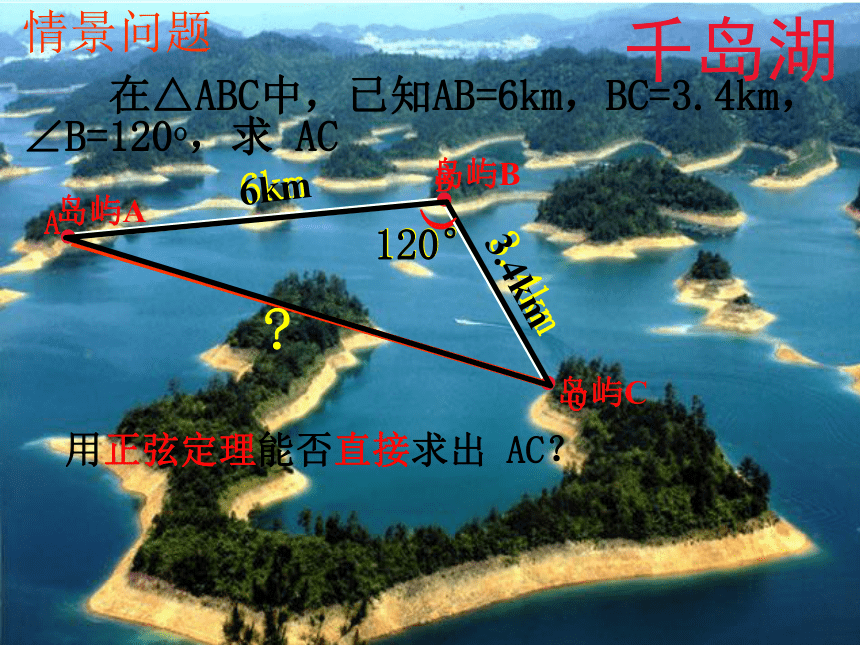
在△ABC中,已知AB=6km,BC=3.4km,∠B=120o,求 AC
用正弦定理能否直接求出 AC?
)
余弦定理
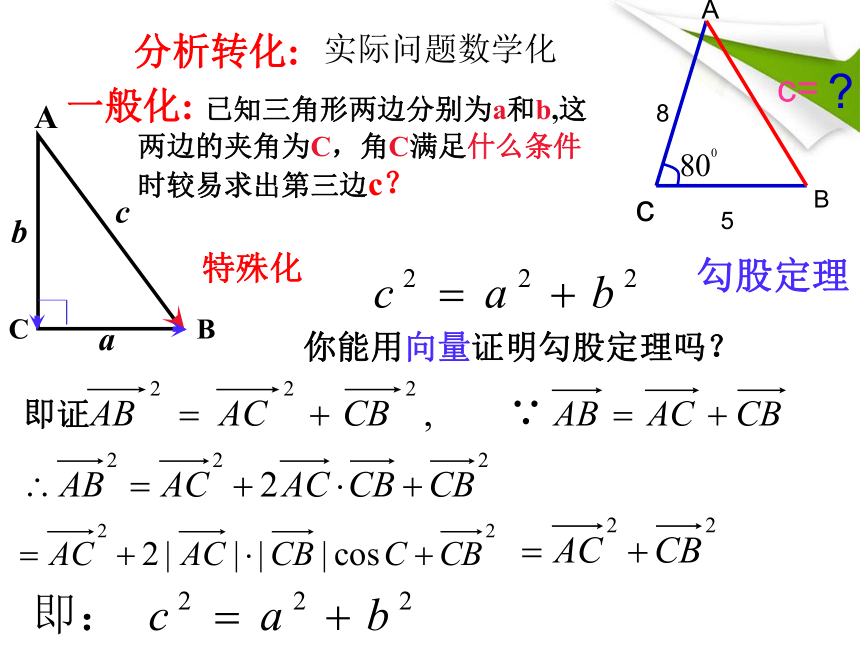
实际问题数学化
分析转化:
c=
一般化:
A
B
C
c
b
a
已知三角形两边分别为a和b,这两边的夹角为C,角C满足什么条件时较易求出第三边c?
勾股定理
你能用向量证明勾股定理吗?
即证
特殊化
C
B
A
b
c
a
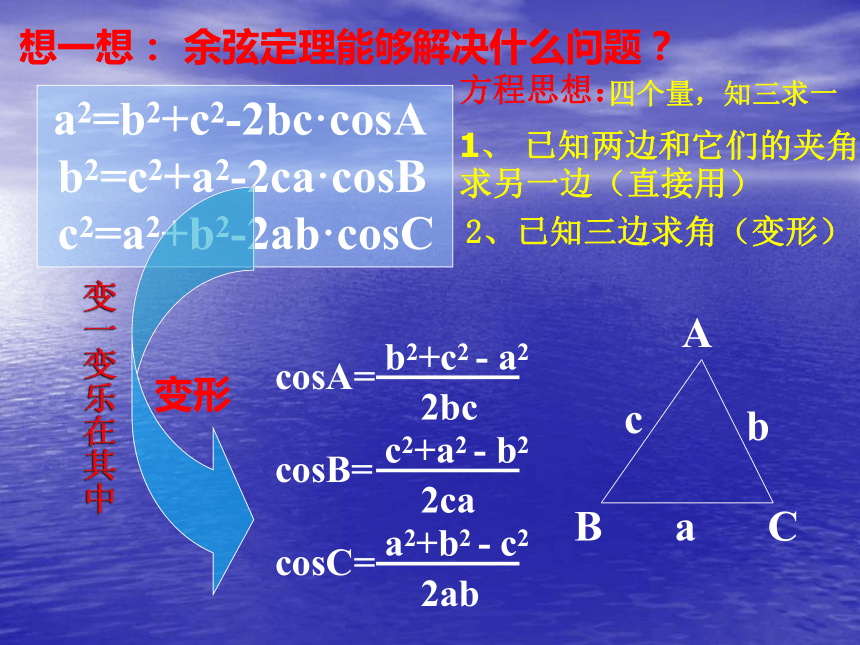
想一想: 余弦定理能够解决什么问题?
a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC
方程思想:
四个量,知三求一
1、 已知两边和它们的夹角求另一边(直接用)
2、已知三边求角(变形)
变形
变一变乐在其中
b2+c2 - a2
2bc
cosA=
c2+a2 - b2
2ca
cosB=
a2+b2 - c2
2ab
cosC=
C
B
A
a
b
c
3.4km
6km
120°
)
A
B
C
在△ABC中,已知AB=6km,BC=3.4km,
∠B=120o,求 AC
解决实际问题
解:由余弦定理得
答:岛屿A与岛屿C的距离为8.24 km.
练习:在△ABC:
(1)已知c=8,b=3,A=60°,求a;
(2)已知a=20,b=29,c=21,求B;
答案:△ABC是一个钝角三角形。
解斜三角形的常见类型及解法
在三角形的6个元素中要已知三个(除三角外)才能求解,常见类型及其解法如表所示.
已知条件 应用定理 一般解法
一边和两角
(如a,B,C)
由A+B+C=180°,求角A;由正弦定理求出b与c.
正弦定理
两边和夹角
(如a,b,C)
三边
(a,b,c)
两边和其中
一边的对角
(如a,b,A)
余弦定理
正弦定理
由余弦定理求第三边c;由正弦定理求出小边所对的角;再由A+B+C=180°求出另一角.
余弦定理
由余弦定理求出角A、B;再利用A+B+C=180°,求出角C.
正弦定理
余弦定理
由正弦定理求出角B;由A+B+C=180°,求出角C;再利用正弦定理或余弦定理求c.
->
千岛湖
3.4km
6km
120°
)
情景问题
岛屿B
岛屿A
岛屿C
千岛湖
千岛湖
情景问题
3.4km
6km
120°
)
岛屿B
岛屿A
岛屿C
3.4km
6km
120°
A
B
C
在△ABC中,已知AB=6km,BC=3.4km,∠B=120o,求 AC
用正弦定理能否直接求出 AC?
)
余弦定理
实际问题数学化
分析转化:
c=
一般化:
A
B
C
c
b
a
已知三角形两边分别为a和b,这两边的夹角为C,角C满足什么条件时较易求出第三边c?
勾股定理
你能用向量证明勾股定理吗?
即证
特殊化
C
B
A
b
c
a
想一想: 余弦定理能够解决什么问题?
a2=b2+c2-2bc·cosA
b2=c2+a2-2ca·cosB
c2=a2+b2-2ab·cosC
方程思想:
四个量,知三求一
1、 已知两边和它们的夹角求另一边(直接用)
2、已知三边求角(变形)
变形
变一变乐在其中
b2+c2 - a2
2bc
cosA=
c2+a2 - b2
2ca
cosB=
a2+b2 - c2
2ab
cosC=
C
B
A
a
b
c
3.4km
6km
120°
)
A
B
C
在△ABC中,已知AB=6km,BC=3.4km,
∠B=120o,求 AC
解决实际问题
解:由余弦定理得
答:岛屿A与岛屿C的距离为8.24 km.
练习:在△ABC:
(1)已知c=8,b=3,A=60°,求a;
(2)已知a=20,b=29,c=21,求B;
答案:△ABC是一个钝角三角形。
解斜三角形的常见类型及解法
在三角形的6个元素中要已知三个(除三角外)才能求解,常见类型及其解法如表所示.
已知条件 应用定理 一般解法
一边和两角
(如a,B,C)
由A+B+C=180°,求角A;由正弦定理求出b与c.
正弦定理
两边和夹角
(如a,b,C)
三边
(a,b,c)
两边和其中
一边的对角
(如a,b,A)
余弦定理
正弦定理
由余弦定理求第三边c;由正弦定理求出小边所对的角;再由A+B+C=180°求出另一角.
余弦定理
由余弦定理求出角A、B;再利用A+B+C=180°,求出角C.
正弦定理
余弦定理
由正弦定理求出角B;由A+B+C=180°,求出角C;再利用正弦定理或余弦定理求c.
->
