解斜三角形实际应用
图片预览



文档简介
(共15张PPT)
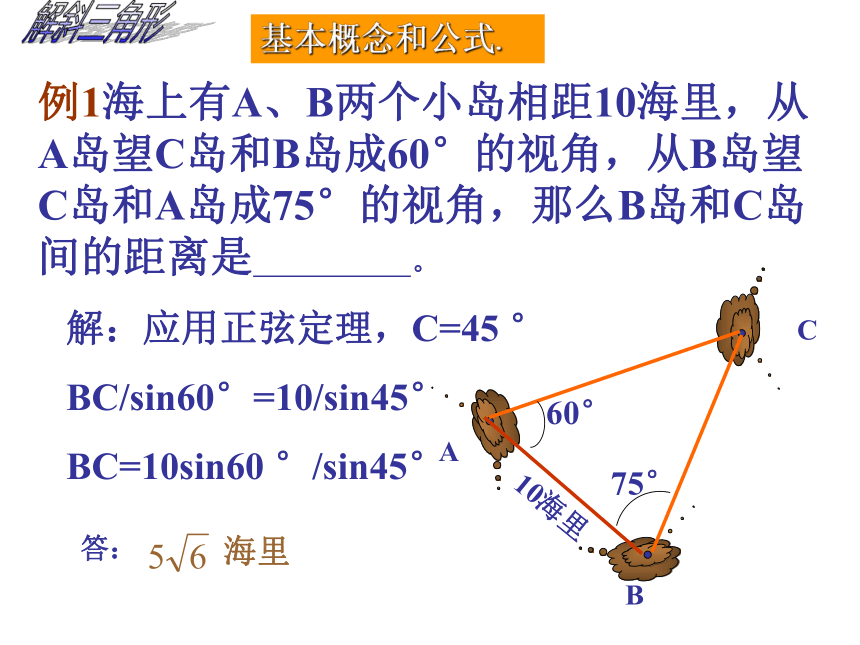
例1海上有A、B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,那么B岛和C岛间的距离是 。
A
C
B
10海里
60°
75°
答:
海里
基本概念和公式.
解:应用正弦定理,C=45 °
BC/sin60°=10/sin45°
BC=10sin60 °/sin45°
基本概念和公式
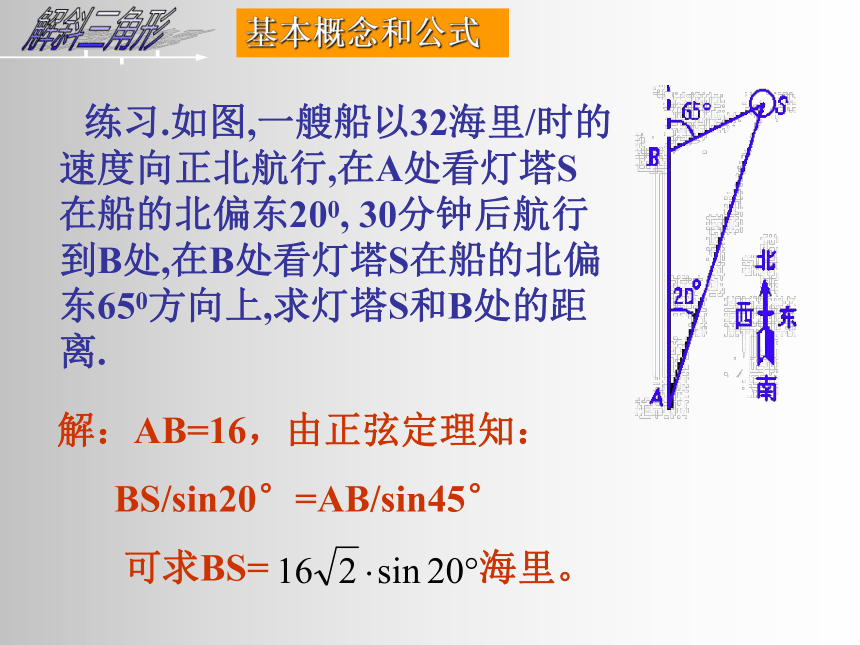
练习.如图,一艘船以32海里/时的速度向正北航行,在A处看灯塔S在船的北偏东200, 30分钟后航行到B处,在B处看灯塔S在船的北偏东650方向上,求灯塔S和B处的距离.
解:AB=16,由正弦定理知:
BS/sin20°=AB/sin45°
可求BS= 海里。
4、计算要认真。
解斜三角形理论应用于实际问题应注意:
1、认真分析题意,弄清已知元素和未知元素。
2、要明确题目中一些名词、术语的意义。如仰角,俯角,方位角等等。
3、动手画出示意图,利用几何图形的性质,将已知和未知集中到一个三角形中解决。
解三角形的应用.
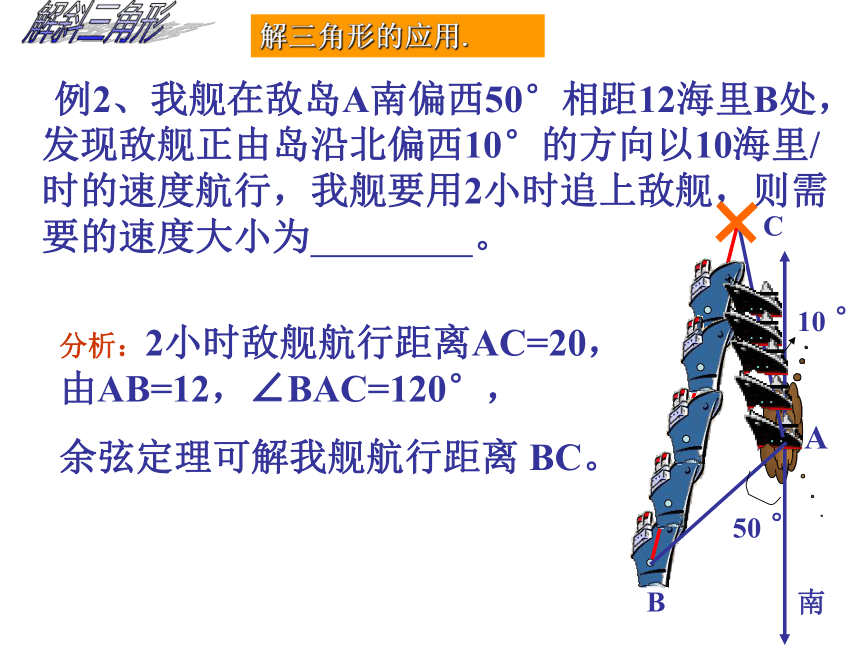
例2、我舰在敌岛A南偏西50°相距12海里B处,发现敌舰正由岛沿北偏西10°的方向以10海里/时的速度航行,我舰要用2小时追上敌舰,则需要的速度大小为 。
A
南
50 °
B
10 °
C
分析:2小时敌舰航行距离AC=20,由AB=12,∠BAC=120°,
余弦定理可解我舰航行距离 BC。
解三角形的应用----
实地测量举例
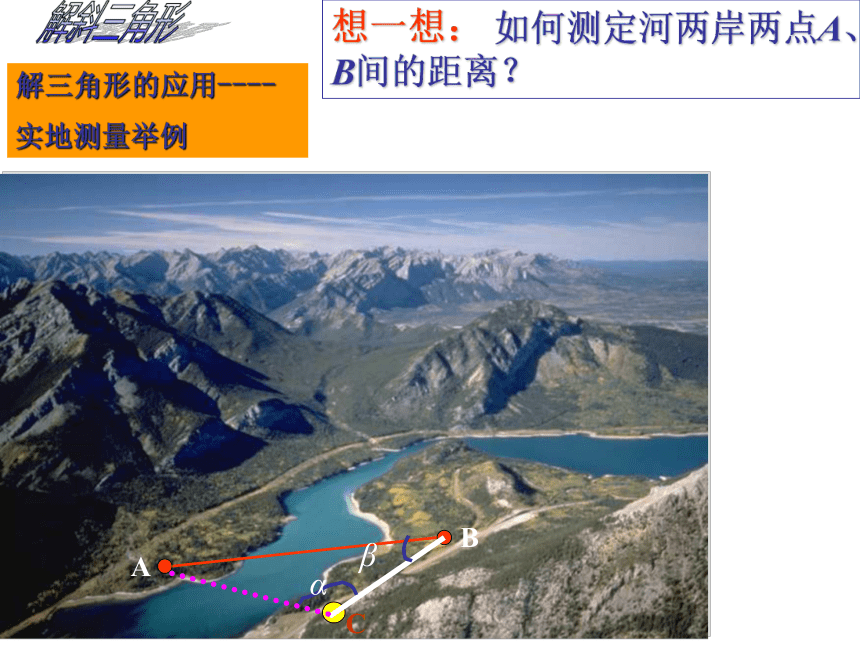
想一想: 如何测定河两岸两点A、B间的距离?
A
B
解三角形的应用----
实地测量举例
想一想: 如何测定河两岸两点A、B间的距离?
A
B
α
β
C
解三角形的应用----
实地测量举例
想一想: 如何测定河两岸两点A、B间的距离?
A
B
α
β
C
A
B
α
β
C
a
简解:由正弦定理可得
AB/sinα=BC/sinA
=a/sin(α+β)
a
解三角形的应用----
实地测量举例
例3、 如何测定河对岸两点A、B间的距离?如图在河这边取一点,构造三角形ABC,能否求出AB 为什么??
A
B
C
解三角形的应用----
实地测量举例
例3、 为了测定河对岸两点A、B间的距离,在岸边选定1公里长的基线CD,并测得∠ACD=90o,∠BCD=60o,∠BDC=75o,∠ADC=30o,求A、B两点的距离.
A
B
C
D
A
B
C
D
1公里
分析:在四边形ABCD中欲求AB长,只能去解三角形,与AB联系的三角形有△ABC和△ABD,利用其一可求AB。
∠ACD=90o,∠BCD=60o,∠BDC=75o,∠ADC=30o,
略解:Rt △ACD中,AD=1/cos30o
△BCD中,1/sin45=BD/sin60,可求BD。
由余弦定理在△ABD中可求AB。
例1海上有A、B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,那么B岛和C岛间的距离是 。
A
C
B
10海里
60°
75°
答:
海里
基本概念和公式.
解:应用正弦定理,C=45 °
BC/sin60°=10/sin45°
BC=10sin60 °/sin45°
基本概念和公式
练习.如图,一艘船以32海里/时的速度向正北航行,在A处看灯塔S在船的北偏东200, 30分钟后航行到B处,在B处看灯塔S在船的北偏东650方向上,求灯塔S和B处的距离.
解:AB=16,由正弦定理知:
BS/sin20°=AB/sin45°
可求BS= 海里。
4、计算要认真。
解斜三角形理论应用于实际问题应注意:
1、认真分析题意,弄清已知元素和未知元素。
2、要明确题目中一些名词、术语的意义。如仰角,俯角,方位角等等。
3、动手画出示意图,利用几何图形的性质,将已知和未知集中到一个三角形中解决。
解三角形的应用.
例2、我舰在敌岛A南偏西50°相距12海里B处,发现敌舰正由岛沿北偏西10°的方向以10海里/时的速度航行,我舰要用2小时追上敌舰,则需要的速度大小为 。
A
南
50 °
B
10 °
C
分析:2小时敌舰航行距离AC=20,由AB=12,∠BAC=120°,
余弦定理可解我舰航行距离 BC。
解三角形的应用----
实地测量举例
想一想: 如何测定河两岸两点A、B间的距离?
A
B
解三角形的应用----
实地测量举例
想一想: 如何测定河两岸两点A、B间的距离?
A
B
α
β
C
解三角形的应用----
实地测量举例
想一想: 如何测定河两岸两点A、B间的距离?
A
B
α
β
C
A
B
α
β
C
a
简解:由正弦定理可得
AB/sinα=BC/sinA
=a/sin(α+β)
a
解三角形的应用----
实地测量举例
例3、 如何测定河对岸两点A、B间的距离?如图在河这边取一点,构造三角形ABC,能否求出AB 为什么??
A
B
C
解三角形的应用----
实地测量举例
例3、 为了测定河对岸两点A、B间的距离,在岸边选定1公里长的基线CD,并测得∠ACD=90o,∠BCD=60o,∠BDC=75o,∠ADC=30o,求A、B两点的距离.
A
B
C
D
A
B
C
D
1公里
分析:在四边形ABCD中欲求AB长,只能去解三角形,与AB联系的三角形有△ABC和△ABD,利用其一可求AB。
∠ACD=90o,∠BCD=60o,∠BDC=75o,∠ADC=30o,
略解:Rt △ACD中,AD=1/cos30o
△BCD中,1/sin45=BD/sin60,可求BD。
由余弦定理在△ABD中可求AB。
