北师大版数学八年级上册教学设计:1.1.2探索勾股定理(第二课时 表格式)
文档属性
| 名称 | 北师大版数学八年级上册教学设计:1.1.2探索勾股定理(第二课时 表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 85.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 00:00:00 | ||
图片预览


文档简介
逸夫中学电子备课本
年级
八年级
学科
数
学
姓名
2019---2020学年
一
学期
?????八年级??数学???科教学设计
课
题
探索勾股定理(第2课时)
课
时
第1课时
主备教师
研讨时间
9.6
执行教师
上课时间
9.7
教学目标
知识与技能:掌握勾股定理及其验证,并能应用勾股定理解决一些实际问题.?
过程与方法:在上节课对具体的直角三角形探索发现了勾股定理的基础上,经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想.
2通过拼图验证勾股定理并体会其中数形结合的思想;应用勾股定理解决一些实际问题培养学生应用数学解决实际问题意识和能力
感态度价值观:在勾股定理的验证活动中,培养探究能力和合作精神;通过对勾股定理历史的了解,感受数学文化,增强爱国情感,并通过应用勾股定理解决实际问题,培养应用数学的意识.
教学重点
用面积法验证勾股定理,应用勾股定理解决简单的实际问题是本节课的重点.
教学难点
应用勾股定理解决一些实际问题,体会勾股定理的应用价值
教具使用
多媒体演示
教法选择
思考-探索-发现-归纳
教
学
过
程
教师活动
学生活动
个性思考
一、第一环节:
复习设疑,激趣引入教师提出问题:(1)勾股定理的内容是什么?(请一名学生回答)(2)上节课我们仅仅是通过测量和数格子,对具体的直角三角形探索发现了勾股定理,对一般的直角三角形,勾股定理是否成立呢?这需要进一步验证,如何验证勾股定理呢?事实上,现在已经有几百种勾股定理的验证方法,这节课我们也将去验证勾股定理.
第二环节:小组活动,拼图验证.
活动1:
教师导入,小组拼图.教师:今天我们将研究利用拼图的方法验证勾股定理,请你利用自己准备的四个全等的直角三角形,拼出一个以斜边为边长的正方形.(请每位同学用2分钟时间独立拼图,然后再4人小组讨论.)
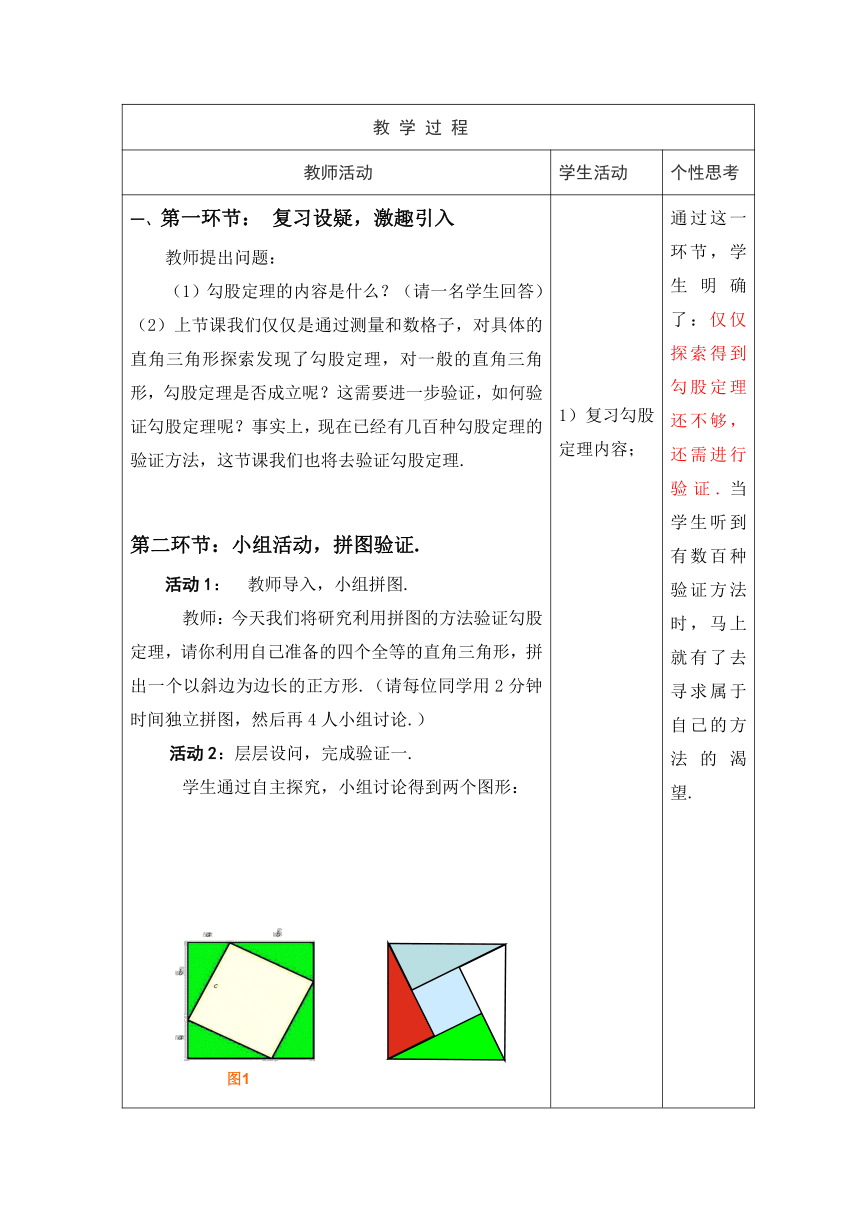
活动2:层层设问,完成验证一.学生通过自主探究,小组讨论得到两个图形:
在此基础上教师提问:(1)如图1你能表示大正方形的面积吗?能用两种方法吗?(学生先独立思考,再4人小组交流);(2)你能由此得到勾股定理吗?为什么?(在学生回答的基础上板书(a+b)2=4×ab+c2.并得到)从而利用图1验证了勾股定理.
活动3
:
自主探究,完成验证教师小结:我们利用拼图的方法,将形的问题与数的问题结合起来,联系整式运算的有关知识,从理论上验证了勾股定理,你还能利用图2验证勾股定理吗?(学生先独立探究,再小组交流,最后请一个小组同学上台讲解验证方法二)
1)复习勾股定理内容;(2)回顾上节课探索过程,强调仍需对一般的直角三角形进行验证,培养学生严谨的科学态度;用图形割补法进行验证(3)介绍世界上有数百种验证方法,激发学生兴趣.
通过这一环节,学生明确了:仅仅探索得到勾股定理还不够,还需进行验证.当学生听到有数百种验证方法时,马上就有了去寻求属于自己的方法的渴望.我们拼图的方法,将形的问题与数的问题结合起来,联系整式运算的有关知识,从理论上验证了勾股定理
第三环节
延伸拓展,能力提升1.议一议:观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2一个直角三角形的斜边为20cm?,且两直角边长度比为3:4,求两直角边的长。第四环节:
例题讲解
初步应用例题:飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩子头顶5000米,飞机每小时飞行多少千米?
第五环节:
回顾反思
提炼升华
教师提问:通过这节课的学习,你有什么样的收获?师生共同畅谈收获.
\
第六环节:
布置作业,课堂延伸教师布置作业1.习题1.2
1,2,3
2.上网或查阅有关书籍,搜集至少1种勾股定理的其它证法,至少1个勾股定理的应用问题,一周后进行展评.
设计了拼图活动,先让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究得到方法1,最后由学生独立探究得到方法2.
师生共同畅谈收获.
板书设计一、?复习勾股定理:
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用,,分别表示直角三角形的两直角边和斜边,那么.
教学反思
勾股定理作为“千古第一定理”其魅力在于其历史价值和应用价值,因此我注意充分挖掘了其内涵.特别是让学生事先进行调查,再在课堂上进行展示,这极大地调动了学生,既加深了对勾股定理文化的理解,又培养了他们收集、整理资料的能力.勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,我设计了拼图活动,先让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究得到方法,最后由学生独立探究得到方法2.这样学生较容易地突破了本节课的难点.
组内研讨:
如果学生的程度较好可以按照本教学设计进行教学,并且可以把分层练习中“知识拓展”作为课堂教学内容.如果学生程度稍差,可以舍弃第三环节以及第五环节中的(2)(3)两个问题.而把分层练习中“基础训练”作为课堂过关使用.
22
图1
_
b
_
a
_
a
_
c
_
b
_
c
年级
八年级
学科
数
学
姓名
2019---2020学年
一
学期
?????八年级??数学???科教学设计
课
题
探索勾股定理(第2课时)
课
时
第1课时
主备教师
研讨时间
9.6
执行教师
上课时间
9.7
教学目标
知识与技能:掌握勾股定理及其验证,并能应用勾股定理解决一些实际问题.?
过程与方法:在上节课对具体的直角三角形探索发现了勾股定理的基础上,经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想.
2通过拼图验证勾股定理并体会其中数形结合的思想;应用勾股定理解决一些实际问题培养学生应用数学解决实际问题意识和能力
感态度价值观:在勾股定理的验证活动中,培养探究能力和合作精神;通过对勾股定理历史的了解,感受数学文化,增强爱国情感,并通过应用勾股定理解决实际问题,培养应用数学的意识.
教学重点
用面积法验证勾股定理,应用勾股定理解决简单的实际问题是本节课的重点.
教学难点
应用勾股定理解决一些实际问题,体会勾股定理的应用价值
教具使用
多媒体演示
教法选择
思考-探索-发现-归纳
教
学
过
程
教师活动
学生活动
个性思考
一、第一环节:
复习设疑,激趣引入教师提出问题:(1)勾股定理的内容是什么?(请一名学生回答)(2)上节课我们仅仅是通过测量和数格子,对具体的直角三角形探索发现了勾股定理,对一般的直角三角形,勾股定理是否成立呢?这需要进一步验证,如何验证勾股定理呢?事实上,现在已经有几百种勾股定理的验证方法,这节课我们也将去验证勾股定理.
第二环节:小组活动,拼图验证.
活动1:
教师导入,小组拼图.教师:今天我们将研究利用拼图的方法验证勾股定理,请你利用自己准备的四个全等的直角三角形,拼出一个以斜边为边长的正方形.(请每位同学用2分钟时间独立拼图,然后再4人小组讨论.)
活动2:层层设问,完成验证一.学生通过自主探究,小组讨论得到两个图形:
在此基础上教师提问:(1)如图1你能表示大正方形的面积吗?能用两种方法吗?(学生先独立思考,再4人小组交流);(2)你能由此得到勾股定理吗?为什么?(在学生回答的基础上板书(a+b)2=4×ab+c2.并得到)从而利用图1验证了勾股定理.
活动3
:
自主探究,完成验证教师小结:我们利用拼图的方法,将形的问题与数的问题结合起来,联系整式运算的有关知识,从理论上验证了勾股定理,你还能利用图2验证勾股定理吗?(学生先独立探究,再小组交流,最后请一个小组同学上台讲解验证方法二)
1)复习勾股定理内容;(2)回顾上节课探索过程,强调仍需对一般的直角三角形进行验证,培养学生严谨的科学态度;用图形割补法进行验证(3)介绍世界上有数百种验证方法,激发学生兴趣.
通过这一环节,学生明确了:仅仅探索得到勾股定理还不够,还需进行验证.当学生听到有数百种验证方法时,马上就有了去寻求属于自己的方法的渴望.我们拼图的方法,将形的问题与数的问题结合起来,联系整式运算的有关知识,从理论上验证了勾股定理
第三环节
延伸拓展,能力提升1.议一议:观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2一个直角三角形的斜边为20cm?,且两直角边长度比为3:4,求两直角边的长。第四环节:
例题讲解
初步应用例题:飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩子头顶5000米,飞机每小时飞行多少千米?
第五环节:
回顾反思
提炼升华
教师提问:通过这节课的学习,你有什么样的收获?师生共同畅谈收获.
\
第六环节:
布置作业,课堂延伸教师布置作业1.习题1.2
1,2,3
2.上网或查阅有关书籍,搜集至少1种勾股定理的其它证法,至少1个勾股定理的应用问题,一周后进行展评.
设计了拼图活动,先让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究得到方法1,最后由学生独立探究得到方法2.
师生共同畅谈收获.
板书设计一、?复习勾股定理:
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用,,分别表示直角三角形的两直角边和斜边,那么.
教学反思
勾股定理作为“千古第一定理”其魅力在于其历史价值和应用价值,因此我注意充分挖掘了其内涵.特别是让学生事先进行调查,再在课堂上进行展示,这极大地调动了学生,既加深了对勾股定理文化的理解,又培养了他们收集、整理资料的能力.勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,我设计了拼图活动,先让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究得到方法,最后由学生独立探究得到方法2.这样学生较容易地突破了本节课的难点.
组内研讨:
如果学生的程度较好可以按照本教学设计进行教学,并且可以把分层练习中“知识拓展”作为课堂教学内容.如果学生程度稍差,可以舍弃第三环节以及第五环节中的(2)(3)两个问题.而把分层练习中“基础训练”作为课堂过关使用.
22
图1
_
b
_
a
_
a
_
c
_
b
_
c
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
