23.3 课题学习 图案设计同步练习(含答案)
文档属性
| 名称 | 23.3 课题学习 图案设计同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十三章 旋转
23.3 课题学习 图案设计
练习
一、单选题(共10小题)
1.(2020·衡水市期中)在图示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是(?)
A. B. C. D..
2.(2018·烟台市期中)如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A.3种 B.4种 C.5种 D.6种
3.(2018·邢台市期末)将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A. B. C. D.
4.(2020·邯郸市期中)如图,同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,其中菱形AEFG可以看成是把菱形ABCD以点A为中心( )
A.逆时针旋转120°得到 B.逆时针旋转60°得到
C.顺时针旋转120°得到 D.顺时针旋转60°得到
5.(2019·贵港市期末)如图的四个图形中,由基础图形通过平移、旋转或轴对称这三种变换都能得到的是( )
A. B. C. D.
6.(2018·重庆市期末)如图,图(1)中的三角形有8个,图(2)中的三角形有14个,图(3)中的三角形有20个,…,则图(8)中的三角形有( )
A.48个 B.50个 C.56个 D.64个
7.(2019百色市期末)下列图案可以通过一个“基本图形”平移得到的是( )
A. B.C.D.
8.(2019·北京市期中)彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样,穿越时空,向人们呈现出古代中国丰富多彩的物质与精神世界,各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起,形成复杂而精美的图案.以下图案纹样中,从整体观察(个别细微之处的细节忽略不计),大致运用了旋转进行构图的是( ).
A. B.
C. D.
9.(2019·洋县期中)下列四组图形都含有两个可以重合的三角形,其中可以通过平移其中一个三角形得到另一个三角形的是( )
A. B.
C. D.
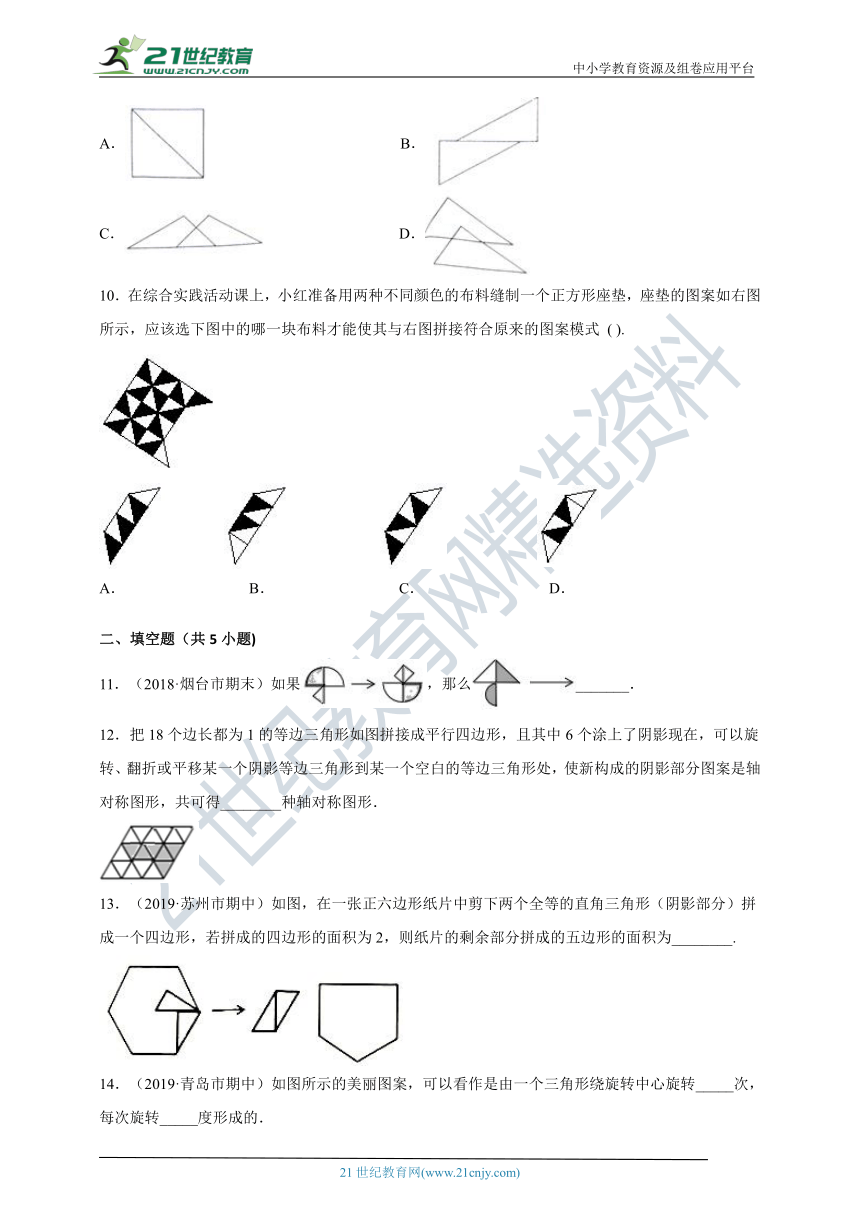
10.在综合实践活动课上,小红准备用两种不同颜色的布料缝制一个正方形座垫,座垫的图案如右图所示,应该选下图中的哪一块布料才能使其与右图拼接符合原来的图案模式 ( ).
A. B. C. D.
二、填空题(共5小题)
11.(2018·烟台市期末)如果,那么_______.
12.把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得________种轴对称图形.
13.(2019·苏州市期中)如图,在一张正六边形纸片中剪下两个全等的直角三角形(阴影部分)拼成一个四边形,若拼成的四边形的面积为2,则纸片的剩余部分拼成的五边形的面积为________.
14.(2019·青岛市期中)如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转_____次,每次旋转_____度形成的.
15.(2018·泉州市期末)如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:______.
三、解答题(共2小题)
16.(2020·台儿庄市期末)在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
17.(2019·温州市期末)如图,图1、图2是两张大小完全相同的6×6方格纸,每个小方格的顶点叫做格点,以格点为顶点的多边形叫做格点多边形.网格中有一个边长为2的格点正方形,按下列要求画出拼图后的格点平行四边形(用阴影表示)
(1)把图1中的格点正方形分割成两部分,再通过图形变换拼成一个平行四边形,在图1中画出这个格点平行四边形;
(2)把图2中的格点正方形分割成三部分,再通过图形变换拼成一个平行四边形,在图2中画出这个格点平行四边形.
答案
一、单选题(共10小题)
1.D.2.C.3.B.4.A.5.B.6.B.7.B.8.B.9.D.10.C.
二、填空题(共5小题)
11.【答案】.【详解】
解:由题意可知,先旋转了,上半部分再作轴对称变换,可得图形:
12.【答案】【详解】
解:∵把六个等边三角形分别经过旋转、翻折或平移可以得到的轴对称图形有:
∴共可得到种轴对称图形
故答案是:
13.【答案】10【详解】如图所示:
将正六边形可分为12个全等的直角三角形,
∵拼成的四边形的面积为2,即阴影部分的面积为2,
∴每一个直角三角形的面积为1,
∴剩余部分的面积为10.
故答案为:10.
14【答案】7 45 【详解】
解:利用旋转中的三个要素(①旋转中心;?②旋转方向;?③旋转角度)设计图案,进而判断出基本图形和旋转次数与角度.故如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转次,每次旋转度形成的,
故答案为:;.
15.【答案】△ABC绕C点逆时针旋转90°,并向左平移2个单位得到△DEF
【解析】
由图可知,把△ABC绕点O逆时针旋转90°可得到△DEF.
三、解答题(共2小题)
16.【答案】见解析.【详解】
解:根据剪掉其中两个方格,使之成为轴对称图形;即如图所示:
17.【答案】(1)见解析;(2)见解析【详解】
(1)解:如图1中,平行四边形ABCD即为所求(答案不唯一)
(2)解:如图2中平行四边形ABCD即为所求( 答案不唯一 )
_21?????????è?????(www.21cnjy.com)_
第二十三章 旋转
23.3 课题学习 图案设计
练习
一、单选题(共10小题)
1.(2020·衡水市期中)在图示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是(?)
A. B. C. D..
2.(2018·烟台市期中)如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A.3种 B.4种 C.5种 D.6种
3.(2018·邢台市期末)将一个正方形纸片按如图1、图2依次对折后,再按如图3打出一个心形小孔,则展开铺平后的图案是( )
A. B. C. D.
4.(2020·邯郸市期中)如图,同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的,其中菱形AEFG可以看成是把菱形ABCD以点A为中心( )
A.逆时针旋转120°得到 B.逆时针旋转60°得到
C.顺时针旋转120°得到 D.顺时针旋转60°得到
5.(2019·贵港市期末)如图的四个图形中,由基础图形通过平移、旋转或轴对称这三种变换都能得到的是( )
A. B. C. D.
6.(2018·重庆市期末)如图,图(1)中的三角形有8个,图(2)中的三角形有14个,图(3)中的三角形有20个,…,则图(8)中的三角形有( )
A.48个 B.50个 C.56个 D.64个
7.(2019百色市期末)下列图案可以通过一个“基本图形”平移得到的是( )
A. B.C.D.
8.(2019·北京市期中)彩陶、玉器、青铜器等器物以及壁画、织锦上美轮美奂的纹样,穿越时空,向人们呈现出古代中国丰富多彩的物质与精神世界,各种纹样经常通过平移、旋转、轴对称以及其它几何构架连接在一起,形成复杂而精美的图案.以下图案纹样中,从整体观察(个别细微之处的细节忽略不计),大致运用了旋转进行构图的是( ).
A. B.
C. D.
9.(2019·洋县期中)下列四组图形都含有两个可以重合的三角形,其中可以通过平移其中一个三角形得到另一个三角形的是( )
A. B.
C. D.
10.在综合实践活动课上,小红准备用两种不同颜色的布料缝制一个正方形座垫,座垫的图案如右图所示,应该选下图中的哪一块布料才能使其与右图拼接符合原来的图案模式 ( ).
A. B. C. D.
二、填空题(共5小题)
11.(2018·烟台市期末)如果,那么_______.
12.把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得________种轴对称图形.
13.(2019·苏州市期中)如图,在一张正六边形纸片中剪下两个全等的直角三角形(阴影部分)拼成一个四边形,若拼成的四边形的面积为2,则纸片的剩余部分拼成的五边形的面积为________.
14.(2019·青岛市期中)如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转_____次,每次旋转_____度形成的.
15.(2018·泉州市期末)如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:______.
三、解答题(共2小题)
16.(2020·台儿庄市期末)在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
17.(2019·温州市期末)如图,图1、图2是两张大小完全相同的6×6方格纸,每个小方格的顶点叫做格点,以格点为顶点的多边形叫做格点多边形.网格中有一个边长为2的格点正方形,按下列要求画出拼图后的格点平行四边形(用阴影表示)
(1)把图1中的格点正方形分割成两部分,再通过图形变换拼成一个平行四边形,在图1中画出这个格点平行四边形;
(2)把图2中的格点正方形分割成三部分,再通过图形变换拼成一个平行四边形,在图2中画出这个格点平行四边形.
答案
一、单选题(共10小题)
1.D.2.C.3.B.4.A.5.B.6.B.7.B.8.B.9.D.10.C.
二、填空题(共5小题)
11.【答案】.【详解】
解:由题意可知,先旋转了,上半部分再作轴对称变换,可得图形:
12.【答案】【详解】
解:∵把六个等边三角形分别经过旋转、翻折或平移可以得到的轴对称图形有:
∴共可得到种轴对称图形
故答案是:
13.【答案】10【详解】如图所示:
将正六边形可分为12个全等的直角三角形,
∵拼成的四边形的面积为2,即阴影部分的面积为2,
∴每一个直角三角形的面积为1,
∴剩余部分的面积为10.
故答案为:10.
14【答案】7 45 【详解】
解:利用旋转中的三个要素(①旋转中心;?②旋转方向;?③旋转角度)设计图案,进而判断出基本图形和旋转次数与角度.故如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转次,每次旋转度形成的,
故答案为:;.
15.【答案】△ABC绕C点逆时针旋转90°,并向左平移2个单位得到△DEF
【解析】
由图可知,把△ABC绕点O逆时针旋转90°可得到△DEF.
三、解答题(共2小题)
16.【答案】见解析.【详解】
解:根据剪掉其中两个方格,使之成为轴对称图形;即如图所示:
17.【答案】(1)见解析;(2)见解析【详解】
(1)解:如图1中,平行四边形ABCD即为所求(答案不唯一)
(2)解:如图2中平行四边形ABCD即为所求( 答案不唯一 )
_21?????????è?????(www.21cnjy.com)_
同课章节目录
