23.1 图形的旋转同步练习题(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十三章 旋转
23.1 图形的旋转
练习
一、单选题(共10小题)
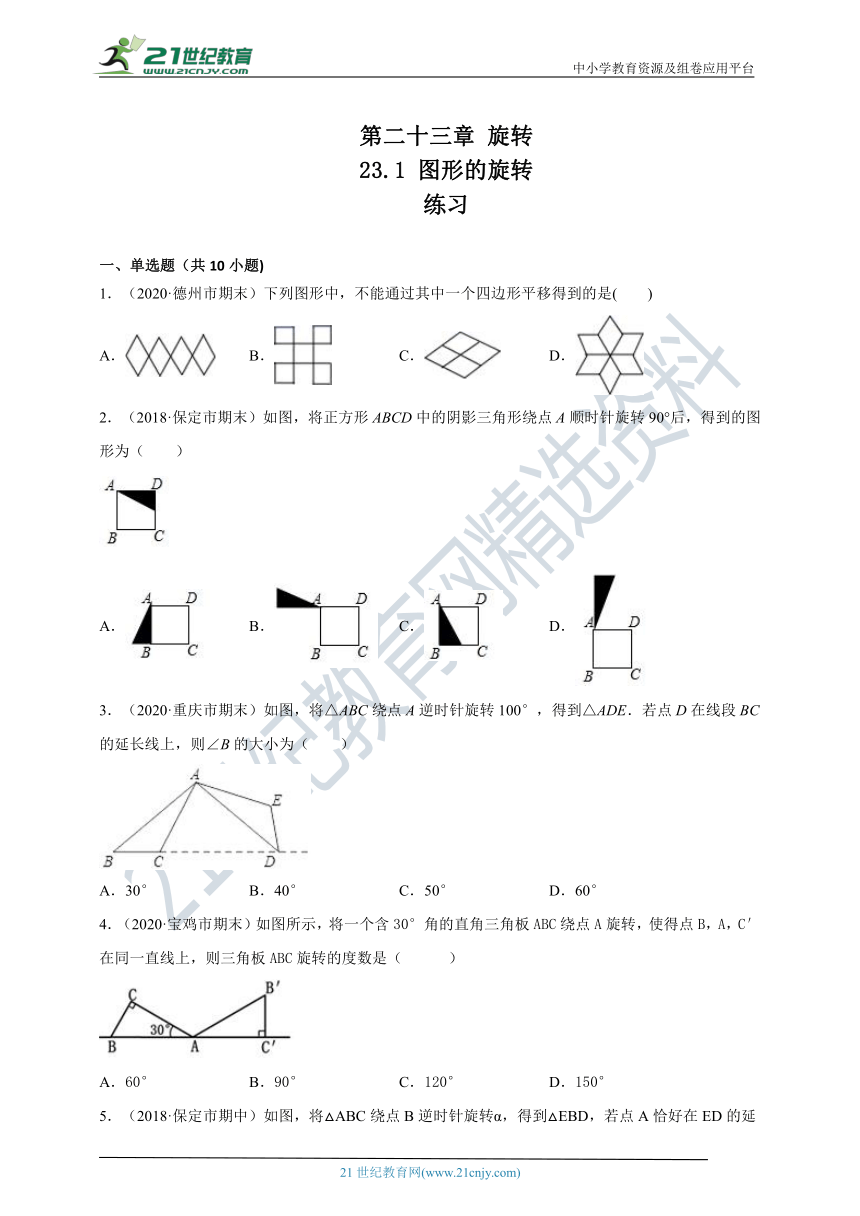
1.(2020·德州市期末)下列图形中,不能通过其中一个四边形平移得到的是( )
A. B. C. D.
2.(2018·保定市期末)如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
A. B. C. D.
3.(2020·重庆市期末)如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )
A.30° B.40° C.50° D.60°
4.(2020·宝鸡市期末)如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是( )
A.60° B.90° C.120° D.150°
5.(2018·保定市期中)如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
6.(2020·扬州市期中)在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
7.(2020·武威市期末)如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( )
A.42° B.48°
C.52° D.58°
8.(2019·天津市期末)如图,将△ABC绕点C顺时针旋转,点B的对应点为点E,点A的对应点为点D,当点E恰好落在边AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是( )
A. B. C. D.
9.(2020·乌鲁木齐市期末)如图,将绕点逆时针旋转70°到的位置,若,则( )
A.45° B.40° C.35° D.30°
10.(2020·佛山市期末)如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.点M B.格点N C.格点P D.格点Q
二、填空题(共5小题)
11.(2020·惠州市期末)如图,把△ABC绕点C按顺时针方向旋转35°,得到△A’B’C,A’B’交AC于点D,若∠A’DC=90°,则∠A= °.
12.(2020·深圳市期中)如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=_____度.
13.(2019·徐州市期末)如图,将三个同样的正方形的一个顶点重合放置,那么的度数为__________.
14.(2019·孟津县期中)如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
15.(2019·沧州市期末)如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为_____.
三、解答题(共2小题)
16.(2019·锦州市期末)在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
17.(2019·南昌市期中)如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.
答案
一、单选题(共10小题)
1.D.2.A。3.B.4.D.5.C.6.B.7.A8.D.9.D10.B.
二、填空题(共5小题)
11.【答案】55.【详解】试题分析:∵把△ABC绕点C按顺时针方向旋转35°,得到△A’B’C
∴∠ACA’=35°,∠A =∠A’,.
∵∠A’DC=90°,
∴∠A’ =55°.
∴∠A=55°.
12.【答案】30°【详解】∵将△AOB绕点O按逆时针方向旋转45°后,得到△COD,
∴∠BOD=45°,
又∵∠AOB=15°,
∴∠AOD=∠BOD-∠AOB=45°-15°=30°.
故答案为30°.
13. 【答案】20°.【详解】
解:如图:∠BOD=90°-∠A0B=90°-30°=60°
∠EOC=90°-∠EOF=90°-40°=50°
又:∠1=∠BOD+∠EOC-∠BOE
∠1=60°+50°-90°=20°
故答案是:20°.
14.【答案】17°【详解】解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50°?33°=17°.
故答案为17°.
15.【答案】60°【解析】试题解析:∵∠ACB=90°,∠ABC=30°,
∴∠A=90°-30°=60°,
∵△ABC绕点C顺时针旋转至△A′B′C时点A′恰好落在AB上,
∴AC=A′C,
∴△A′AC是等边三角形,
∴∠ACA′=60°,
∴旋转角为60°.
故答案为60°.
三、解答题(共2小题)
16.【答案】(1)作图见解析,C1的坐标C1(-1,2), C2的坐标C2(-3,-2);(2)y=-x.
详解:(1)如图所示, C1的坐标C1(-1,2), C2的坐标C2(-3,-2)
(2)解:∵A(2,4),A3(-4,-2),
∴直线l的函数解析式:y=-x.
17.【答案】(1)详见解析;(2)详见解析.
【详解】
(1)由旋转的性质得,CD=CF,∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠BCD+∠DCE=90°,
∴∠BCD=∠ECF,
在△BDC和△EFC中,
,
∴△BDC≌△EFC(SAS);
(2)∵EF∥CD,
∴∠F+∠DCF=180°,
∵∠DCF=90°,
∴∠F=90°,
∵△BDC≌△EFC,
∴∠BDC=∠F=90°.
_21?????????è?????(www.21cnjy.com)_
第二十三章 旋转
23.1 图形的旋转
练习
一、单选题(共10小题)
1.(2020·德州市期末)下列图形中,不能通过其中一个四边形平移得到的是( )
A. B. C. D.
2.(2018·保定市期末)如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
A. B. C. D.
3.(2020·重庆市期末)如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )
A.30° B.40° C.50° D.60°
4.(2020·宝鸡市期末)如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是( )
A.60° B.90° C.120° D.150°
5.(2018·保定市期中)如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
6.(2020·扬州市期中)在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
7.(2020·武威市期末)如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( )
A.42° B.48°
C.52° D.58°
8.(2019·天津市期末)如图,将△ABC绕点C顺时针旋转,点B的对应点为点E,点A的对应点为点D,当点E恰好落在边AC上时,连接AD,若∠ACB=30°,则∠DAC的度数是( )
A. B. C. D.
9.(2020·乌鲁木齐市期末)如图,将绕点逆时针旋转70°到的位置,若,则( )
A.45° B.40° C.35° D.30°
10.(2020·佛山市期末)如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.点M B.格点N C.格点P D.格点Q
二、填空题(共5小题)
11.(2020·惠州市期末)如图,把△ABC绕点C按顺时针方向旋转35°,得到△A’B’C,A’B’交AC于点D,若∠A’DC=90°,则∠A= °.
12.(2020·深圳市期中)如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=_____度.
13.(2019·徐州市期末)如图,将三个同样的正方形的一个顶点重合放置,那么的度数为__________.
14.(2019·孟津县期中)如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
15.(2019·沧州市期末)如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为_____.
三、解答题(共2小题)
16.(2019·锦州市期末)在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
17.(2019·南昌市期中)如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.
答案
一、单选题(共10小题)
1.D.2.A。3.B.4.D.5.C.6.B.7.A8.D.9.D10.B.
二、填空题(共5小题)
11.【答案】55.【详解】试题分析:∵把△ABC绕点C按顺时针方向旋转35°,得到△A’B’C
∴∠ACA’=35°,∠A =∠A’,.
∵∠A’DC=90°,
∴∠A’ =55°.
∴∠A=55°.
12.【答案】30°【详解】∵将△AOB绕点O按逆时针方向旋转45°后,得到△COD,
∴∠BOD=45°,
又∵∠AOB=15°,
∴∠AOD=∠BOD-∠AOB=45°-15°=30°.
故答案为30°.
13. 【答案】20°.【详解】
解:如图:∠BOD=90°-∠A0B=90°-30°=60°
∠EOC=90°-∠EOF=90°-40°=50°
又:∠1=∠BOD+∠EOC-∠BOE
∠1=60°+50°-90°=20°
故答案是:20°.
14.【答案】17°【详解】解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50°?33°=17°.
故答案为17°.
15.【答案】60°【解析】试题解析:∵∠ACB=90°,∠ABC=30°,
∴∠A=90°-30°=60°,
∵△ABC绕点C顺时针旋转至△A′B′C时点A′恰好落在AB上,
∴AC=A′C,
∴△A′AC是等边三角形,
∴∠ACA′=60°,
∴旋转角为60°.
故答案为60°.
三、解答题(共2小题)
16.【答案】(1)作图见解析,C1的坐标C1(-1,2), C2的坐标C2(-3,-2);(2)y=-x.
详解:(1)如图所示, C1的坐标C1(-1,2), C2的坐标C2(-3,-2)
(2)解:∵A(2,4),A3(-4,-2),
∴直线l的函数解析式:y=-x.
17.【答案】(1)详见解析;(2)详见解析.
【详解】
(1)由旋转的性质得,CD=CF,∠DCF=90°,
∴∠DCE+∠ECF=90°,
∵∠ACB=90°,
∴∠BCD+∠DCE=90°,
∴∠BCD=∠ECF,
在△BDC和△EFC中,
,
∴△BDC≌△EFC(SAS);
(2)∵EF∥CD,
∴∠F+∠DCF=180°,
∵∠DCF=90°,
∴∠F=90°,
∵△BDC≌△EFC,
∴∠BDC=∠F=90°.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
