人教版 九年级 上册 24.3正多边形和圆 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版 九年级 上册 24.3正多边形和圆 同步练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 183.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-23 00:00:00 | ||
图片预览

文档简介
正多边形和圆同步练习
一、选择题
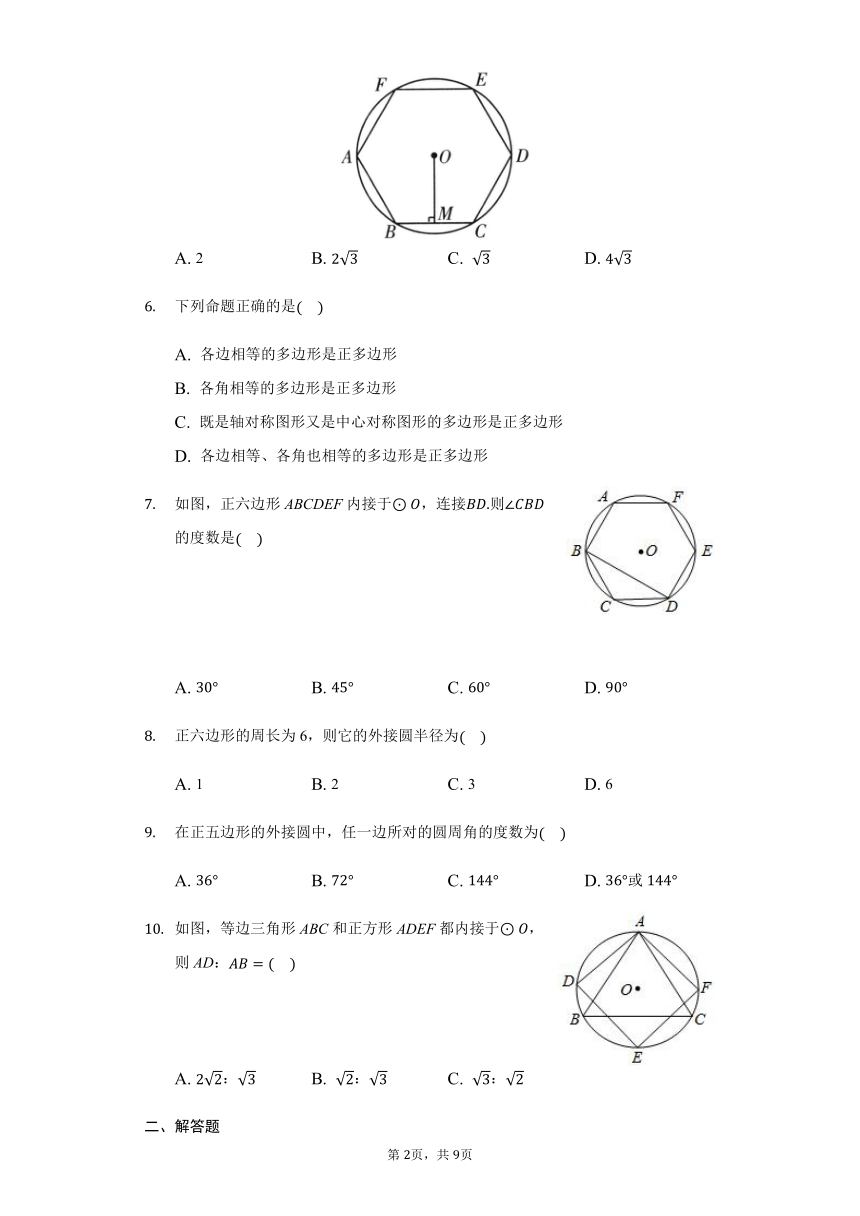
如图,点P是正六边形ABCDEF内部一个动点,,则点P到这个正六边形六条边的距离之和为.
A.
6
B.
3
C.
D.
校园内有一个由两个全等的正六边形边长为围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为?
?
A.
B.
C.
D.
正九边形不具有的性质是?
?
A.
外角为
B.
一定有外接圆
C.
是轴对称图形
D.
是中心对称图形
一个正多边形的中心角为,它的边心距为a,则它的半径为
A.
B.
C.
D.
4a
如图,正六边形ABCDEF内接于,半径为4,则这个正六边形的边心距OM的长为?
?
?
A.
2
B.
C.
D.
下列命题正确的是
A.
各边相等的多边形是正多边形
B.
各角相等的多边形是正多边形
C.
既是轴对称图形又是中心对称图形的多边形是正多边形
D.
各边相等、各角也相等的多边形是正多边形
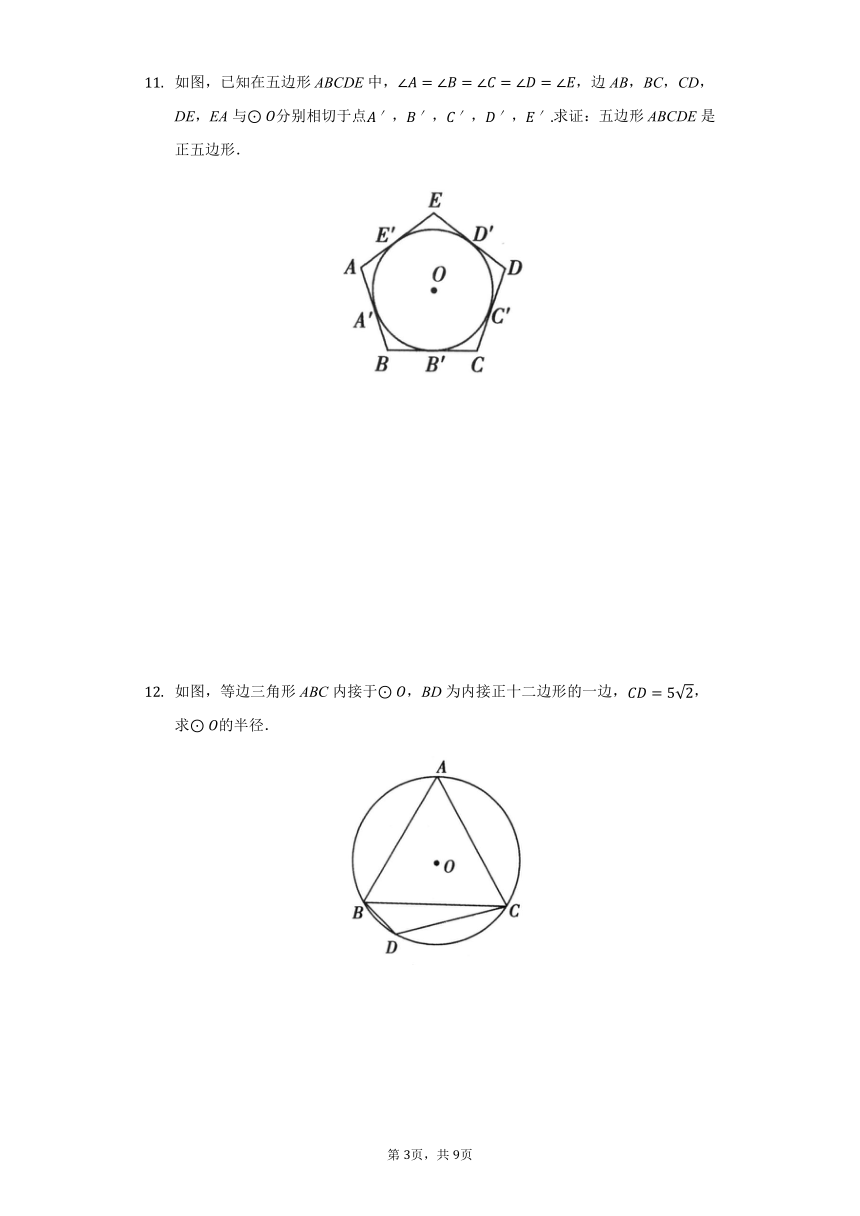
如图,正六边形ABCDEF内接于,连接则的度数是
A.
B.
C.
D.
正六边形的周长为6,则它的外接圆半径为
A.
1
B.
2
C.
3
D.
6
在正五边形的外接圆中,任一边所对的圆周角的度数为
A.
B.
C.
D.
或
如图,等边三角形ABC和正方形ADEF都内接于,则AD:
A.
:
B.
:
C.
:
D.
:
二、解答题
如图,已知在五边形ABCDE中,,边AB,BC,CD,DE,EA与分别相切于点,,,,求证:五边形ABCDE是正五边形.
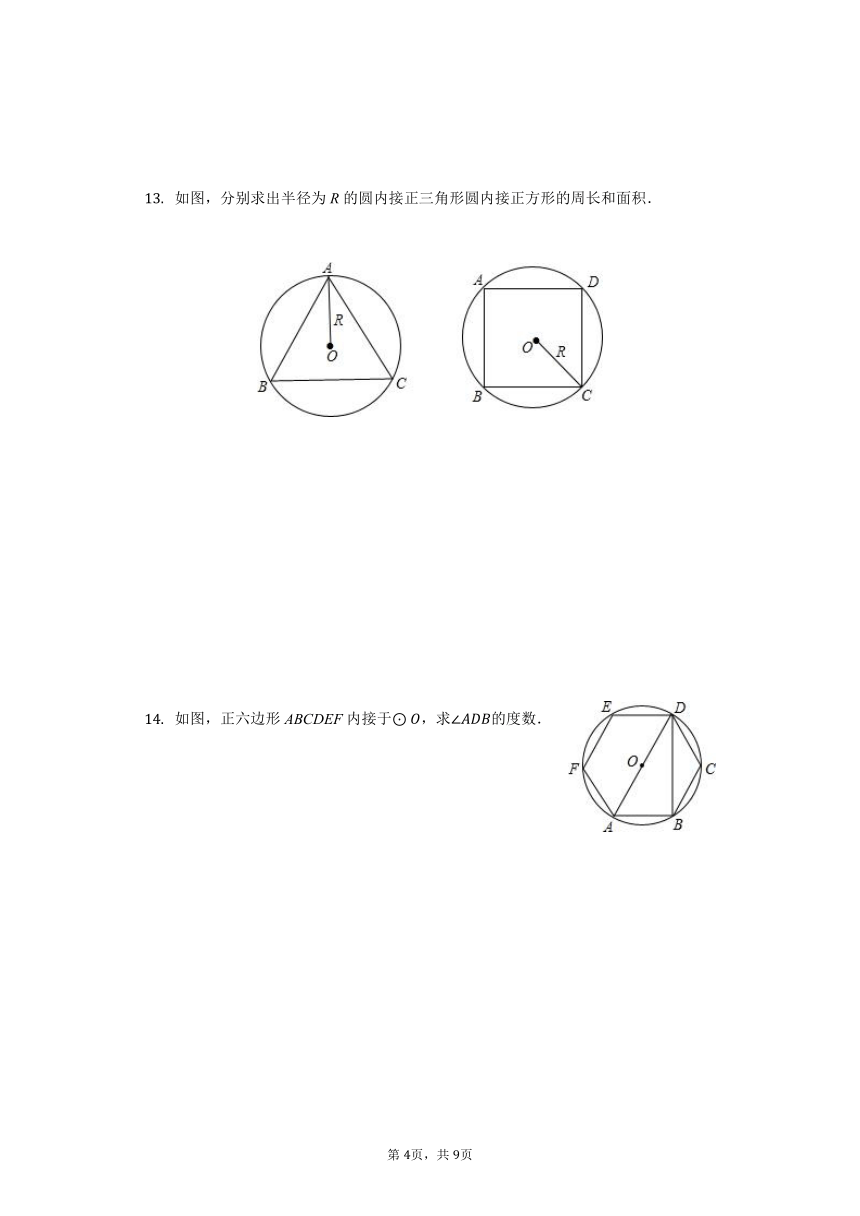
如图,等边三角形ABC内接于,BD为内接正十二边形的一边,,求的半径.
如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
如图,正六边形ABCDEF内接于,求的度数.
答案和解析
1.C
解:如图,当点P是正六边形的中心时,
连接PB、PC,过点P作于点H,延长HP交EF于点G,
则点P到这个正六边形六条边的距离之和即为6PH的长.
根据正六边形的性质可知:
是等边三角形,
,
,
,,
,
.
点P到这个正六边形六条边的距离之和为.
2.C
解:如图,
花坛是由两个相同的正六边形围成,
,,
,
是等边三角形,
,
同理可证:,
,
扩建后菱形区域的周长为,
3.D
解:正九边形的每一个外角都是,故此选项不合题意;
B.所有的正多边形一定有外接圆,因此正九边形一定有外接圆,故此选项不合题意;
C.所有的正多边形都是轴对称图形,因此正九边形是轴对称图形,故此选项不合题意;
D.正九边形不是中心对称图形,故此选项合题意.
4.A
解:正多边形的边数是,即正多边形是正方形.
如图,正方形的边心距就是其内切圆的半径OA,即a,
则半径是.
5.B
解:如图,连接OB,OC.
因为多边形ABCDEF是正六边形,所以,
因为,所以是等边三角形,
所以,,
所以,
所以.
故选B.
6.D
解:各边相等、各角也相等的多边形是正多边形,故A,B错误,D正确
矩形既是轴对称图形又是中心对称图形,但其不是正多边形,故C错误.
7.A
解:在正六边形ABCDEF中,
,,
,
8.A
解:正六边形的周长是6,
其边长.
正六边形的边长与其外接圆半径恰好组成等边三角形,
它的外接圆半径是1.
故选:A.
9.D
解:连接OA、OB、BD、AD,在上取点F,连接AF、BF,如图所示:
五边形ABCDE是正五边形,
,,
,
,
即在正五边形的外接圆中,任一边所对的圆周角的度数为或;
10.B
解:连接OA、OB、OD,过O作于H,如图所示:
则,
正方形ADEF和等边三角形ABC都内接于,
,,
,
是等腰直角三角形,,
,,
,
,
故选:B.
连接OA、OB、OD,过O作于H,由垂径定理得出,证出是等腰直角三角形,,,得出,,则,进而得出答案.
11.证明:如图,连接OA,OB,OC,,,,
由题意,得,,
同理,
又,,
.
又,,
同理,,同理,
又,
五边形ABCDE是正五边形.
12.解:设的半径为如图,连接OB,OC,OD.
则,.
.
在中,根据勾股定理,得,
.
13.解:如图1,连接OB、OC,过O作于D,
是正三角形ABC的外接圆,
,
,
,
在中,,,,
,
,
正的周长是;面积是;
如图2,连接OA、OB、OD,
是正方形ABCD的外接圆,
,
,由勾股定理得;,
正方形ABCD的周长为,面积为.
14.解:连接OB,
六边形ABCDEF是正六边形,
,
.
第2页,共2页
第1页,共1页
一、选择题
如图,点P是正六边形ABCDEF内部一个动点,,则点P到这个正六边形六条边的距离之和为.
A.
6
B.
3
C.
D.
校园内有一个由两个全等的正六边形边长为围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为?
?
A.
B.
C.
D.
正九边形不具有的性质是?
?
A.
外角为
B.
一定有外接圆
C.
是轴对称图形
D.
是中心对称图形
一个正多边形的中心角为,它的边心距为a,则它的半径为
A.
B.
C.
D.
4a
如图,正六边形ABCDEF内接于,半径为4,则这个正六边形的边心距OM的长为?
?
?
A.
2
B.
C.
D.
下列命题正确的是
A.
各边相等的多边形是正多边形
B.
各角相等的多边形是正多边形
C.
既是轴对称图形又是中心对称图形的多边形是正多边形
D.
各边相等、各角也相等的多边形是正多边形
如图,正六边形ABCDEF内接于,连接则的度数是
A.
B.
C.
D.
正六边形的周长为6,则它的外接圆半径为
A.
1
B.
2
C.
3
D.
6
在正五边形的外接圆中,任一边所对的圆周角的度数为
A.
B.
C.
D.
或
如图,等边三角形ABC和正方形ADEF都内接于,则AD:
A.
:
B.
:
C.
:
D.
:
二、解答题
如图,已知在五边形ABCDE中,,边AB,BC,CD,DE,EA与分别相切于点,,,,求证:五边形ABCDE是正五边形.
如图,等边三角形ABC内接于,BD为内接正十二边形的一边,,求的半径.
如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
如图,正六边形ABCDEF内接于,求的度数.
答案和解析
1.C
解:如图,当点P是正六边形的中心时,
连接PB、PC,过点P作于点H,延长HP交EF于点G,
则点P到这个正六边形六条边的距离之和即为6PH的长.
根据正六边形的性质可知:
是等边三角形,
,
,
,,
,
.
点P到这个正六边形六条边的距离之和为.
2.C
解:如图,
花坛是由两个相同的正六边形围成,
,,
,
是等边三角形,
,
同理可证:,
,
扩建后菱形区域的周长为,
3.D
解:正九边形的每一个外角都是,故此选项不合题意;
B.所有的正多边形一定有外接圆,因此正九边形一定有外接圆,故此选项不合题意;
C.所有的正多边形都是轴对称图形,因此正九边形是轴对称图形,故此选项不合题意;
D.正九边形不是中心对称图形,故此选项合题意.
4.A
解:正多边形的边数是,即正多边形是正方形.
如图,正方形的边心距就是其内切圆的半径OA,即a,
则半径是.
5.B
解:如图,连接OB,OC.
因为多边形ABCDEF是正六边形,所以,
因为,所以是等边三角形,
所以,,
所以,
所以.
故选B.
6.D
解:各边相等、各角也相等的多边形是正多边形,故A,B错误,D正确
矩形既是轴对称图形又是中心对称图形,但其不是正多边形,故C错误.
7.A
解:在正六边形ABCDEF中,
,,
,
8.A
解:正六边形的周长是6,
其边长.
正六边形的边长与其外接圆半径恰好组成等边三角形,
它的外接圆半径是1.
故选:A.
9.D
解:连接OA、OB、BD、AD,在上取点F,连接AF、BF,如图所示:
五边形ABCDE是正五边形,
,,
,
,
即在正五边形的外接圆中,任一边所对的圆周角的度数为或;
10.B
解:连接OA、OB、OD,过O作于H,如图所示:
则,
正方形ADEF和等边三角形ABC都内接于,
,,
,
是等腰直角三角形,,
,,
,
,
故选:B.
连接OA、OB、OD,过O作于H,由垂径定理得出,证出是等腰直角三角形,,,得出,,则,进而得出答案.
11.证明:如图,连接OA,OB,OC,,,,
由题意,得,,
同理,
又,,
.
又,,
同理,,同理,
又,
五边形ABCDE是正五边形.
12.解:设的半径为如图,连接OB,OC,OD.
则,.
.
在中,根据勾股定理,得,
.
13.解:如图1,连接OB、OC,过O作于D,
是正三角形ABC的外接圆,
,
,
,
在中,,,,
,
,
正的周长是;面积是;
如图2,连接OA、OB、OD,
是正方形ABCD的外接圆,
,
,由勾股定理得;,
正方形ABCD的周长为,面积为.
14.解:连接OB,
六边形ABCDEF是正六边形,
,
.
第2页,共2页
第1页,共1页
同课章节目录
