24.2.2 直线与圆的位置关系(第四课时 三角形的内切圆)同步练习题(含答案)
文档属性
| 名称 | 24.2.2 直线与圆的位置关系(第四课时 三角形的内切圆)同步练习题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.2.2 直线与圆的位置关系(第四课时 三角形的内切圆)
练习
一、单选题(共10小题)
1.(2019·昆明市期中)如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
2.(2019唐山市期末)如图为4×4的正方形网格,A,B,C,D,O均在格点上,点O是( )
A.△ACD的外心 B.△ABC的外心 C.△ACD的内心 D.△ABC的内心
3.(2018·长沙市期中)《九章算术》是我国古代内容极为丰富的数学名著.书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是“今有直角三角形(如图),勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
A.3步 B.5步 C.6步 D.8步
4.(2020·晋中市期末)如图点I是△ABC的内心,∠BIC=130°,则∠BAC=( )
A.65 B.50 C.80 D.100°
5.(2019·恩施市期末)三角形内切圆的圆心是( )
A.三条高的交点 B.三条中线的交点
C.三条角平分线的交点 D.三条边的垂直平分线的交点
6.(2018·兴仁市期末)如图,点O是△ABC的内切圆的圆心,若∠A=80°,则∠BOC为( )
A.100° B.130°
C.50° D.65°
7.(2020·宁波市期末)如图的的网格图,A、B、C、D、O都在格点上,点O是( )
A.的外心 B.的外心 C.的内心 D.的内心
8.(2020·濮阳市期末)如图,点I是△ABC的内心,∠BIC=130°,则∠BAC=( )
A.60° B.65° C.70° D.80°
9.(2018·溧水县期中)如图,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F.若BF=2,AF=3,则△ABC的面积是( )
A.6 B.7 C.12 D.7
10.(2020·河北区期末)已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为的是( )
A. B. C. D.
二、填空题(共5小题)
11.(2019·南通市期中)直角三角形的两条直角边分别是5和12,则它的内切圆半径为_____.
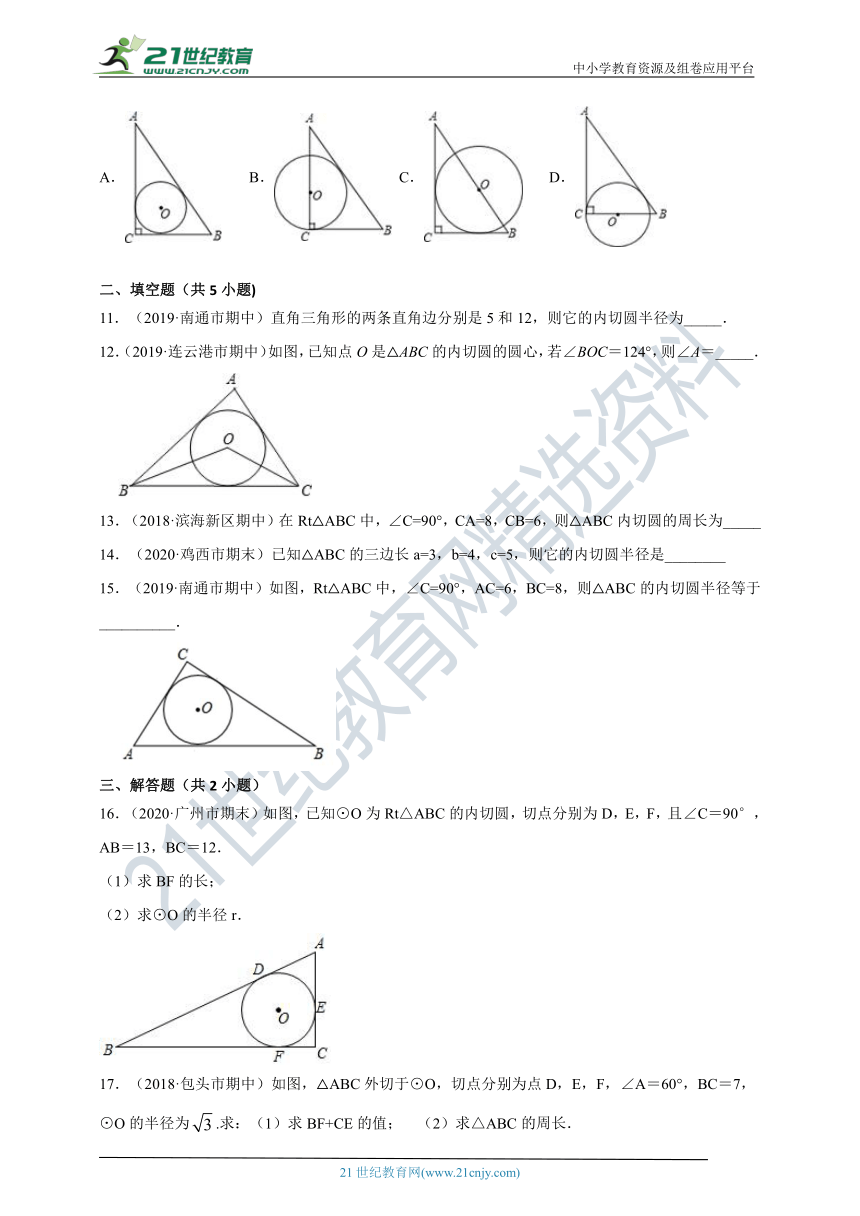
12.(2019·连云港市期中)如图,已知点O是△ABC的内切圆的圆心,若∠BOC=124°,则∠A=_____.
13.(2018·滨海新区期中)在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为_____
14.(2020·鸡西市期末)已知△ABC的三边长a=3,b=4,c=5,则它的内切圆半径是________
15.(2019·南通市期中)如图,Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆半径等于__________.
三、解答题(共2小题)
16.(2020·广州市期末)如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.
(1)求BF的长;
(2)求⊙O的半径r.
17.(2018·包头市期中)如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为.求:(1)求BF+CE的值; (2)求△ABC的周长.
答案
一、单选题(共10小题)
1.B.2.B.3.C4.C.5.C.6.B.7.B.8.D.9.A.10.C.
二、填空题(共5小题)
11.【答案】2【详解】直角三角形的斜边,所以它的内切圆半径.
故答案为2.
12.【答案】68°【详解】解:∵∠BOC=124°,∴∠OBC+∠OCB=180°﹣124°=56°,
∵点O是△ABC的内切圆的圆心∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=112°,∴∠A=180°﹣112°=68°,
故答案为:68°.
13.【答案】4π.【解析】∵∠C=90°,CA=8,CB=6,∴AB==10,
∴△ABC的内切圆的半径==2,
∴△ABC内切圆的周长=2π?2=4π.故答案为4π.
14.【答案】1【解析】
∵a=3,b=4,c=5,
∴a2+b2=c2,
∴∠ACB=90°,
设△ABC的内切圆切AC于E,切AB于F,切BC于D,连接OE、OF、OD、OA、OC、OB,内切圆的半径为R,则OE=OF=OD=R,∵S△ACB=S△AOC+S△AOB+S△BOC,∴×AC×BC=×AC×OE+×AB×OF+×BC×OD,
∴3×4=4R+5R+3R,解得:R=1.故答案为1.
15.【答案】2【详解】如图,
在Rt△ABC,∠C=90°,AC=6,BC=8;
根据勾股定理AB==10;
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°;
∴四边形OECF是正方形;
由切线长定理,得:AD=AF,BD=BE,CE=CF;
∴CE=CF=(AC+BC?AB);
即:r=(6+8?10)=2.
故答案是:2.
三、解答题(共2小题)
16.【答案】(1)BF=10;(2)r=2.【详解】
解:(1)在Rt△ABC中,∵∠C=90°,AB=13,BC=12,
∴AC===5,
∵⊙O为Rt△ABC的内切圆,切点分别为D,E,F,
∴BD=BF,AD=AE,CF=CE,
设BF=BD=x,则AD=AE=13﹣x,CFCE=12﹣x,
∵AE+EC=5,
∴13﹣x+12﹣x=5,
∴x=10,
∴BF=10.
(2)连接OE,OF,
∵OE⊥AC,OF⊥BC,
∴∠OEC=∠C=∠OFC=90°,
∴四边形OECF是矩形,
∴OE=CF=BC﹣BF=12﹣10=2.
即r=2.
17.【答案】(1)7(2)20【解析】
分析:(1)、根据切线长定理得到BF=BD,CE=CD,代入求出即可;(2)、根据切线长定理得到AE=AF,求出∠OAE=30°,根据含30度得直角三角形和勾股定理求出OA、AE,即可求出答案.
详解:(1)如答图,连结OF,OE,OD, ∵△ABC外切于⊙O,切点分别为D,E,F,
∴BF=BD,CE=CD, ∴BF+CE=BD+CD=BC=7;
(2)如答图,连结OA. ∵△ABC外切于⊙O,切点分别为D,E,F,
∴∠OEA=90°,∵AF=AE,AO=AO,FO=EO, ∴△AFO≌△AEO,∴∠OAE=∠BAC=30°,
∴OA=2OE=2,由勾股定理,得AE=AF===3,
∴△ABC的周长是AB+BC+AC=AF+AE+CE+BF+BC=3+3+7+7=20.
_21?????????è?????(www.21cnjy.com)_
第二十四章 圆
24.2.2 直线与圆的位置关系(第四课时 三角形的内切圆)
练习
一、单选题(共10小题)
1.(2019·昆明市期中)如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
2.(2019唐山市期末)如图为4×4的正方形网格,A,B,C,D,O均在格点上,点O是( )
A.△ACD的外心 B.△ABC的外心 C.△ACD的内心 D.△ABC的内心
3.(2018·长沙市期中)《九章算术》是我国古代内容极为丰富的数学名著.书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是“今有直角三角形(如图),勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
A.3步 B.5步 C.6步 D.8步
4.(2020·晋中市期末)如图点I是△ABC的内心,∠BIC=130°,则∠BAC=( )
A.65 B.50 C.80 D.100°
5.(2019·恩施市期末)三角形内切圆的圆心是( )
A.三条高的交点 B.三条中线的交点
C.三条角平分线的交点 D.三条边的垂直平分线的交点
6.(2018·兴仁市期末)如图,点O是△ABC的内切圆的圆心,若∠A=80°,则∠BOC为( )
A.100° B.130°
C.50° D.65°
7.(2020·宁波市期末)如图的的网格图,A、B、C、D、O都在格点上,点O是( )
A.的外心 B.的外心 C.的内心 D.的内心
8.(2020·濮阳市期末)如图,点I是△ABC的内心,∠BIC=130°,则∠BAC=( )
A.60° B.65° C.70° D.80°
9.(2018·溧水县期中)如图,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F.若BF=2,AF=3,则△ABC的面积是( )
A.6 B.7 C.12 D.7
10.(2020·河北区期末)已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为的是( )
A. B. C. D.
二、填空题(共5小题)
11.(2019·南通市期中)直角三角形的两条直角边分别是5和12,则它的内切圆半径为_____.
12.(2019·连云港市期中)如图,已知点O是△ABC的内切圆的圆心,若∠BOC=124°,则∠A=_____.
13.(2018·滨海新区期中)在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为_____
14.(2020·鸡西市期末)已知△ABC的三边长a=3,b=4,c=5,则它的内切圆半径是________
15.(2019·南通市期中)如图,Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆半径等于__________.
三、解答题(共2小题)
16.(2020·广州市期末)如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.
(1)求BF的长;
(2)求⊙O的半径r.
17.(2018·包头市期中)如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为.求:(1)求BF+CE的值; (2)求△ABC的周长.
答案
一、单选题(共10小题)
1.B.2.B.3.C4.C.5.C.6.B.7.B.8.D.9.A.10.C.
二、填空题(共5小题)
11.【答案】2【详解】直角三角形的斜边,所以它的内切圆半径.
故答案为2.
12.【答案】68°【详解】解:∵∠BOC=124°,∴∠OBC+∠OCB=180°﹣124°=56°,
∵点O是△ABC的内切圆的圆心∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2(∠OBC+∠OCB)=112°,∴∠A=180°﹣112°=68°,
故答案为:68°.
13.【答案】4π.【解析】∵∠C=90°,CA=8,CB=6,∴AB==10,
∴△ABC的内切圆的半径==2,
∴△ABC内切圆的周长=2π?2=4π.故答案为4π.
14.【答案】1【解析】
∵a=3,b=4,c=5,
∴a2+b2=c2,
∴∠ACB=90°,
设△ABC的内切圆切AC于E,切AB于F,切BC于D,连接OE、OF、OD、OA、OC、OB,内切圆的半径为R,则OE=OF=OD=R,∵S△ACB=S△AOC+S△AOB+S△BOC,∴×AC×BC=×AC×OE+×AB×OF+×BC×OD,
∴3×4=4R+5R+3R,解得:R=1.故答案为1.
15.【答案】2【详解】如图,
在Rt△ABC,∠C=90°,AC=6,BC=8;
根据勾股定理AB==10;
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°;
∴四边形OECF是正方形;
由切线长定理,得:AD=AF,BD=BE,CE=CF;
∴CE=CF=(AC+BC?AB);
即:r=(6+8?10)=2.
故答案是:2.
三、解答题(共2小题)
16.【答案】(1)BF=10;(2)r=2.【详解】
解:(1)在Rt△ABC中,∵∠C=90°,AB=13,BC=12,
∴AC===5,
∵⊙O为Rt△ABC的内切圆,切点分别为D,E,F,
∴BD=BF,AD=AE,CF=CE,
设BF=BD=x,则AD=AE=13﹣x,CFCE=12﹣x,
∵AE+EC=5,
∴13﹣x+12﹣x=5,
∴x=10,
∴BF=10.
(2)连接OE,OF,
∵OE⊥AC,OF⊥BC,
∴∠OEC=∠C=∠OFC=90°,
∴四边形OECF是矩形,
∴OE=CF=BC﹣BF=12﹣10=2.
即r=2.
17.【答案】(1)7(2)20【解析】
分析:(1)、根据切线长定理得到BF=BD,CE=CD,代入求出即可;(2)、根据切线长定理得到AE=AF,求出∠OAE=30°,根据含30度得直角三角形和勾股定理求出OA、AE,即可求出答案.
详解:(1)如答图,连结OF,OE,OD, ∵△ABC外切于⊙O,切点分别为D,E,F,
∴BF=BD,CE=CD, ∴BF+CE=BD+CD=BC=7;
(2)如答图,连结OA. ∵△ABC外切于⊙O,切点分别为D,E,F,
∴∠OEA=90°,∵AF=AE,AO=AO,FO=EO, ∴△AFO≌△AEO,∴∠OAE=∠BAC=30°,
∴OA=2OE=2,由勾股定理,得AE=AF===3,
∴△ABC的周长是AB+BC+AC=AF+AE+CE+BF+BC=3+3+7+7=20.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
