人教版数学九年级上册:24.1.2 垂直于弦的直径 教案
文档属性
| 名称 | 人教版数学九年级上册:24.1.2 垂直于弦的直径 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 00:00:00 | ||
图片预览


文档简介
24.1.2 垂直于弦的直径
学习目标:
1.进一步认识圆是轴对称图形.
2.能利用圆的轴对称性,通过探索、归纳、验证得出垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.
3.认识垂径定理及推论在实际中的应用,会用添加辅助线的方法解决问题.
教学过程:
一、情境导入
你知道赵州桥吗?它又名“安济桥”,位于河北省赵县,是我国现存的著名的古代石拱桥,距今已有1400多年了,是隋代开皇大业年间(605~618)由著名将师李春建造的,是我国古代人民勤劳和智慧的结晶.
它的主桥拱是圆弧形,全长50.82米,桥宽约10米,跨度37.4米,拱高7.2米,是当今世界上跨径最大、建造最早的单孔敞肩石拱桥.你知道主桥拱的圆弧所在圆的半径吗?
二、基础知识
垂径定理:垂直于弦的直径平分这条弦,并平分弦所对的两条弧.
符号语言:∵是⊙的直径
又∵
∴
推论:平分弦(不是直径)的直径垂直于弦,并平分弦所对的两条弧
符号语言:∵是⊙的直径
又∵
∴
三、合作探究
探究点一:垂径定理
【类型一】垂径定理的理解
如图所示,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,CD=6cm,则直径AB的长是( )
A.2cm
B.3cm
C.4cm
D.4cm
变式1.如图,在⊙中,弦的长为8,圆心到的距离为3.求⊙的半径。
【类型二】垂径定理的实际应用
如图,一条公路的转弯处是一段圆弧(图中的),点O是这段弧的圆心,C是上一点,OC⊥AB,垂足为D,AB=300m,CD=50m,则这段弯路的半径是________m.
变式1..你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4,拱高(弧的中点到弦的距离)为7.2,你能求出赵州桥主桥拱的半径吗?
探究点二:垂径定理的推论
【类型一】利用垂径定理的推论求角
如图所示,⊙O的弦AB、AC的夹角为50°,M、N分别是、的中点,则∠MON的度数是( )
A.100°
B.110°
C.120°
D.130°
变式1.如图,在⊙中,、为互相垂直且相等的两条弦,于,于.
求证:四边形为正方形。
【类型二】利用垂径定理的推论求边
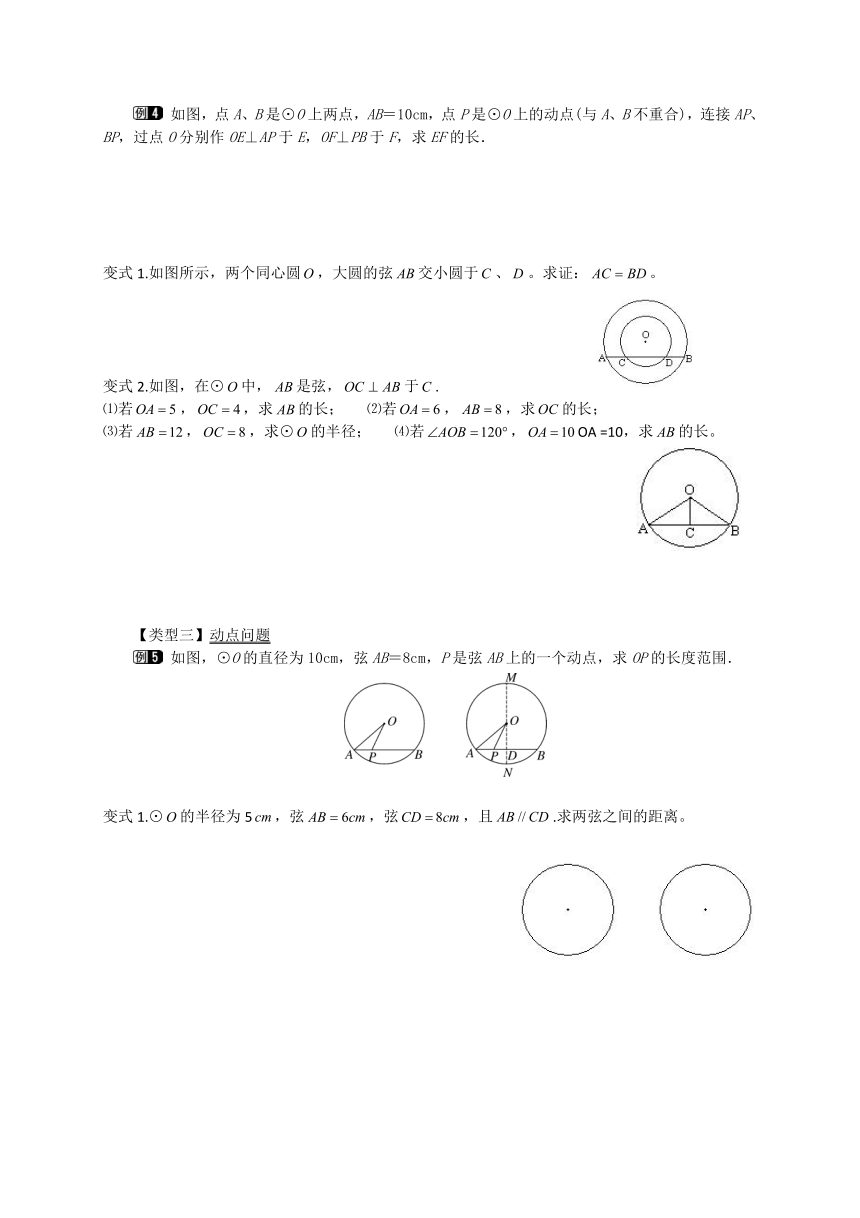
如图,点A、B是⊙O上两点,AB=10cm,点P是⊙O上的动点(与A、B不重合),连接AP、BP,过点O分别作OE⊥AP于E,OF⊥PB于F,求EF的长.
变式1.如图所示,两个同心圆,大圆的弦交小圆于、。求证:。
变式2.如图,在⊙中,是弦,于.
⑴若,,求的长;
⑵若,,求的长;
⑶若,,求⊙的半径;
⑷若,OA
=10,求的长。
【类型三】动点问题
如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
变式1.⊙的半径为5,弦,弦,且.求两弦之间的距离。
4、习题
1.如图,已知的直径于点E,下列结论中一定正确的是(
)
?
2.如图,CD是的直径,AB是弦且不是直径,,则下列结论不一定正确的是(
)
3.如图,圆O的弦中最短的是
.
4.一名伐木工人锯一根圆木,如图,当圆木半径,弦时,则圆木被锯部分的最大高度为
.
5.如图,圆O的直径为,弦AB的长为,P是弦AB上一点,若OP的长是整数,则满足条件的点P有
个.
6.在圆柱形油槽内装有一些油,截面如图所示,直径MN为100cm
,油面宽AB为60cm,如果再注入一些油后,油面宽变为80cm,则油面上升
.
7.如图,是一个圆曲隧道的截面,若路面宽AB为10米,净高CD为7米,则此隧道圆的半径OA是
.
8.如图,两个0为圆心的同心圆,大圆的弦AB交小圆于C,D两点,于H,则图中相等的线段共有
组。
9
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=
。
10.
如图是某风景区的一个圆拱形门,路面AB宽为2m,净高CD为
5m
,则圆拱形门所在圆的半径为________.
11.如图,的弦AB与半径OC垂直,点D为垂足,,点E在上,
,则
的面积为________.
12.如图,的弦AB垂直于CD,E为垂足,且,则圆心O到CD的距离是________.
13.如图,若排水管中水面的宽度米,水深0.2米,则排水管的直径为_____米.
14.如图,CD是的直径,弦为垂足,,则AE=________.
15.如图,已知的半径为5,弦,点E在AB上运动,连结OE,过点E作交于点F,当EF最大时,的值为________.
16.如图,水平放着的圆柱形排水管的截面为,其中水面宽,则水的最大深度为________.
?
17.如图,在中,直径则______。
18.如图,在中,AE是直径,半径,垂足为C,连接CE,若的面积为12,则CD=________.
19.如图,已知AB和CD是的两条弦,且,连接OC,作的平分线交于P,连接,求证:.
20.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.
21、如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.
(1)若OC=5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断直线AD与⊙O的位置关系,并加以证明.
22、如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,
(1)求证:CB∥PD;
(2)若BC=3,sin∠P=,求⊙O的直径.
23、如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.(2)求证:AF=CF.(3)若∠EAB=30°,CF=2,求GA的长.
24.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
学习目标:
1.进一步认识圆是轴对称图形.
2.能利用圆的轴对称性,通过探索、归纳、验证得出垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.
3.认识垂径定理及推论在实际中的应用,会用添加辅助线的方法解决问题.
教学过程:
一、情境导入
你知道赵州桥吗?它又名“安济桥”,位于河北省赵县,是我国现存的著名的古代石拱桥,距今已有1400多年了,是隋代开皇大业年间(605~618)由著名将师李春建造的,是我国古代人民勤劳和智慧的结晶.
它的主桥拱是圆弧形,全长50.82米,桥宽约10米,跨度37.4米,拱高7.2米,是当今世界上跨径最大、建造最早的单孔敞肩石拱桥.你知道主桥拱的圆弧所在圆的半径吗?
二、基础知识
垂径定理:垂直于弦的直径平分这条弦,并平分弦所对的两条弧.
符号语言:∵是⊙的直径
又∵
∴
推论:平分弦(不是直径)的直径垂直于弦,并平分弦所对的两条弧
符号语言:∵是⊙的直径
又∵
∴
三、合作探究
探究点一:垂径定理
【类型一】垂径定理的理解
如图所示,⊙O的直径AB垂直弦CD于点P,且P是半径OB的中点,CD=6cm,则直径AB的长是( )
A.2cm
B.3cm
C.4cm
D.4cm
变式1.如图,在⊙中,弦的长为8,圆心到的距离为3.求⊙的半径。
【类型二】垂径定理的实际应用
如图,一条公路的转弯处是一段圆弧(图中的),点O是这段弧的圆心,C是上一点,OC⊥AB,垂足为D,AB=300m,CD=50m,则这段弯路的半径是________m.
变式1..你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4,拱高(弧的中点到弦的距离)为7.2,你能求出赵州桥主桥拱的半径吗?
探究点二:垂径定理的推论
【类型一】利用垂径定理的推论求角
如图所示,⊙O的弦AB、AC的夹角为50°,M、N分别是、的中点,则∠MON的度数是( )
A.100°
B.110°
C.120°
D.130°
变式1.如图,在⊙中,、为互相垂直且相等的两条弦,于,于.
求证:四边形为正方形。
【类型二】利用垂径定理的推论求边
如图,点A、B是⊙O上两点,AB=10cm,点P是⊙O上的动点(与A、B不重合),连接AP、BP,过点O分别作OE⊥AP于E,OF⊥PB于F,求EF的长.
变式1.如图所示,两个同心圆,大圆的弦交小圆于、。求证:。
变式2.如图,在⊙中,是弦,于.
⑴若,,求的长;
⑵若,,求的长;
⑶若,,求⊙的半径;
⑷若,OA
=10,求的长。
【类型三】动点问题
如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
变式1.⊙的半径为5,弦,弦,且.求两弦之间的距离。
4、习题
1.如图,已知的直径于点E,下列结论中一定正确的是(
)
?
2.如图,CD是的直径,AB是弦且不是直径,,则下列结论不一定正确的是(
)
3.如图,圆O的弦中最短的是
.
4.一名伐木工人锯一根圆木,如图,当圆木半径,弦时,则圆木被锯部分的最大高度为
.
5.如图,圆O的直径为,弦AB的长为,P是弦AB上一点,若OP的长是整数,则满足条件的点P有
个.
6.在圆柱形油槽内装有一些油,截面如图所示,直径MN为100cm
,油面宽AB为60cm,如果再注入一些油后,油面宽变为80cm,则油面上升
.
7.如图,是一个圆曲隧道的截面,若路面宽AB为10米,净高CD为7米,则此隧道圆的半径OA是
.
8.如图,两个0为圆心的同心圆,大圆的弦AB交小圆于C,D两点,于H,则图中相等的线段共有
组。
9
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=
。
10.
如图是某风景区的一个圆拱形门,路面AB宽为2m,净高CD为
5m
,则圆拱形门所在圆的半径为________.
11.如图,的弦AB与半径OC垂直,点D为垂足,,点E在上,
,则
的面积为________.
12.如图,的弦AB垂直于CD,E为垂足,且,则圆心O到CD的距离是________.
13.如图,若排水管中水面的宽度米,水深0.2米,则排水管的直径为_____米.
14.如图,CD是的直径,弦为垂足,,则AE=________.
15.如图,已知的半径为5,弦,点E在AB上运动,连结OE,过点E作交于点F,当EF最大时,的值为________.
16.如图,水平放着的圆柱形排水管的截面为,其中水面宽,则水的最大深度为________.
?
17.如图,在中,直径则______。
18.如图,在中,AE是直径,半径,垂足为C,连接CE,若的面积为12,则CD=________.
19.如图,已知AB和CD是的两条弦,且,连接OC,作的平分线交于P,连接,求证:.
20.如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.
21、如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.
(1)若OC=5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断直线AD与⊙O的位置关系,并加以证明.
22、如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,
(1)求证:CB∥PD;
(2)若BC=3,sin∠P=,求⊙O的直径.
23、如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.(2)求证:AF=CF.(3)若∠EAB=30°,CF=2,求GA的长.
24.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
同课章节目录
