2020-2021学年苏科版八年级数学上册2.4线段、角的轴对称性专题培优训练卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学上册2.4线段、角的轴对称性专题培优训练卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1009.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 08:09:55 | ||
图片预览

文档简介
2020-2021苏科版八年级数学上册2.4线段、角的轴对称性专题培优训练卷
一、选择题
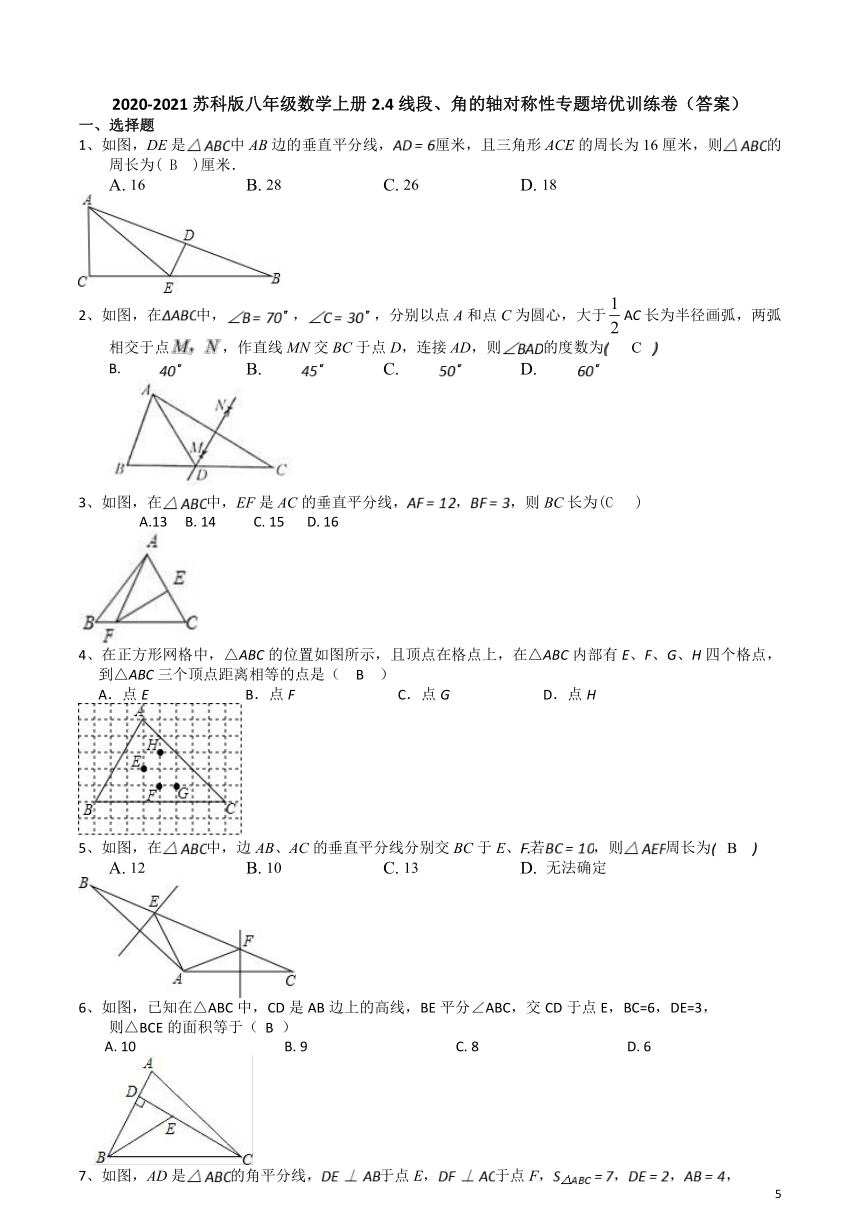
1、如图,DE是中AB边的垂直平分线,厘米,且三角形ACE的周长为16厘米,则的周长为( )厘米.
A. 16 B. 28 C. 26 D. 18
(2) (3)
2、如图,在中,,,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点,作直线MN交BC于点D,连接AD,则的度数为? ? ?
B. C. D.
3、如图,在中,EF是AC的垂直平分线,,,则BC长为( )
A.13 B. 14 C. 15 D. 16
4、在正方形网格中,△ABC的位置如图所示,且顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是( )
A.点E B.点F C.点G D.点H
(5) (6)
5、如图,在中,边AB、AC的垂直平分线分别交BC于E、若,则周长为? ? ?
A. 12 B. 10 C. 13 D. 无法确定
6、如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=6,DE=3,
则△BCE的面积等于(?? )
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
7、如图,AD是的角平分线,于点E,于点F,,,,
则AC的长是( )
A. 6 B. 5 C. 4 D. 3
(8) (9) (10)
8、如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,
则S△ABO︰S△BCO︰S△CAO 等于( ??)
A.?1︰1︰1????????????????????????????B.?1︰2︰3????????????????????????????C.?2︰3︰4????????????????????????????D.?3︰4︰5
9、如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是(?? )
A.?40°???????????????????????????????????????B.?30°???????????????????????????????????????C.?20°???????????????????????????????????????D.?10°
10、如图,在四边形ABCD中,,,BD平分若点P是BC边上一动点,
则DP长的最小值为( )
A. 3 B. 4 C. 5 D. 6
二、填空题
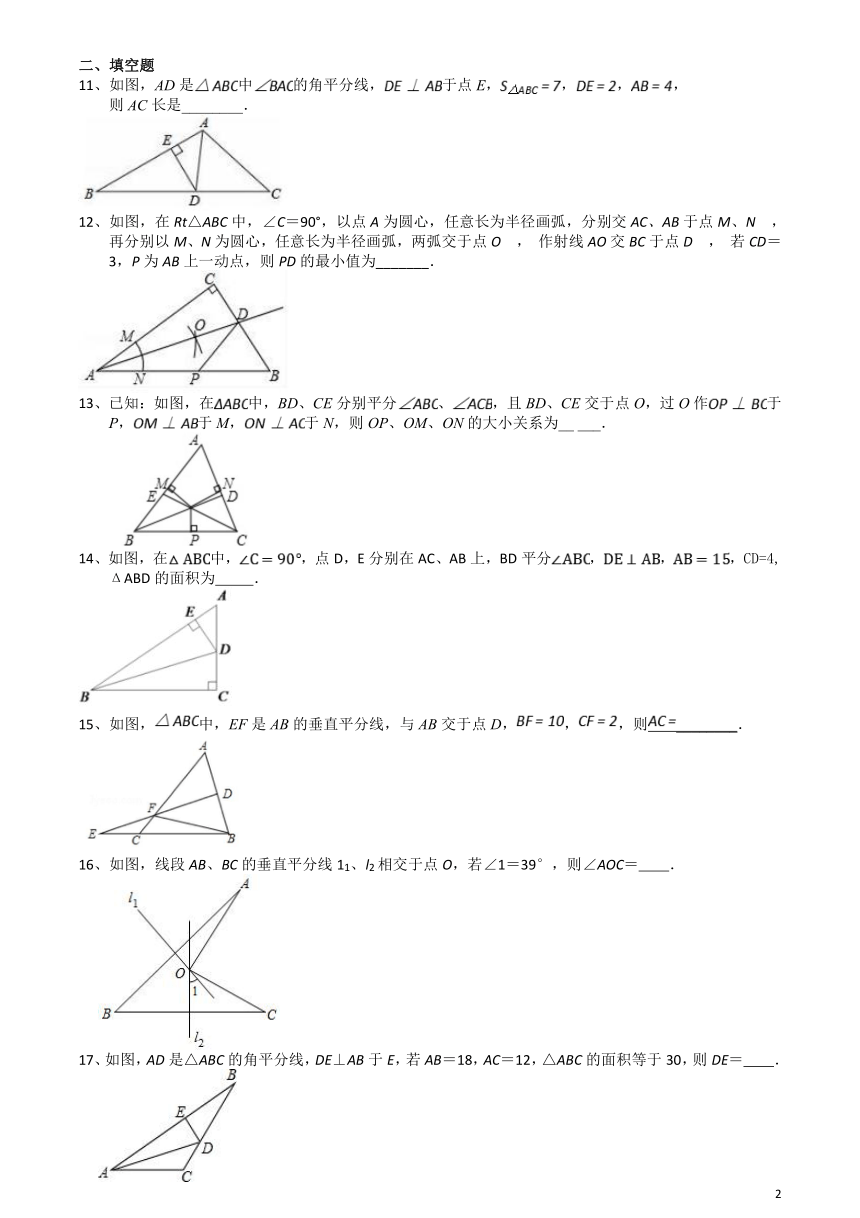
11、如图,AD是中的角平分线,于点E,,,,
则AC长是________.
12、如图,在Rt△ABC中,∠C=90°,以点A为圆心,任意长为半径画弧,分别交AC、AB于点M、N , 再分别以M、N为圆心,任意长为半径画弧,两弧交于点O , 作射线AO交BC于点D , 若CD=3,P为AB上一动点,则PD的最小值为_______.
13、已知:如图,在中,BD、CE分别平分、,且BD、CE交于点O,过O作于P,于M,于N,则OP、OM、ON的大小关系为__ ___.
14、如图,在中,,点D,E分别在AC、AB上,BD平分,,,CD=4,
ΔABD的面积为??????????.
15、如图,中,EF是AB的垂直平分线,与AB交于点D,,,则________.
16、如图,线段AB、BC的垂直平分线11、l2相交于点O,若∠1=39°,则∠AOC= .
17、如图,AD是△ABC的角平分线,DE⊥AB于E,若AB=18,AC=12,△ABC的面积等于30,则DE= .
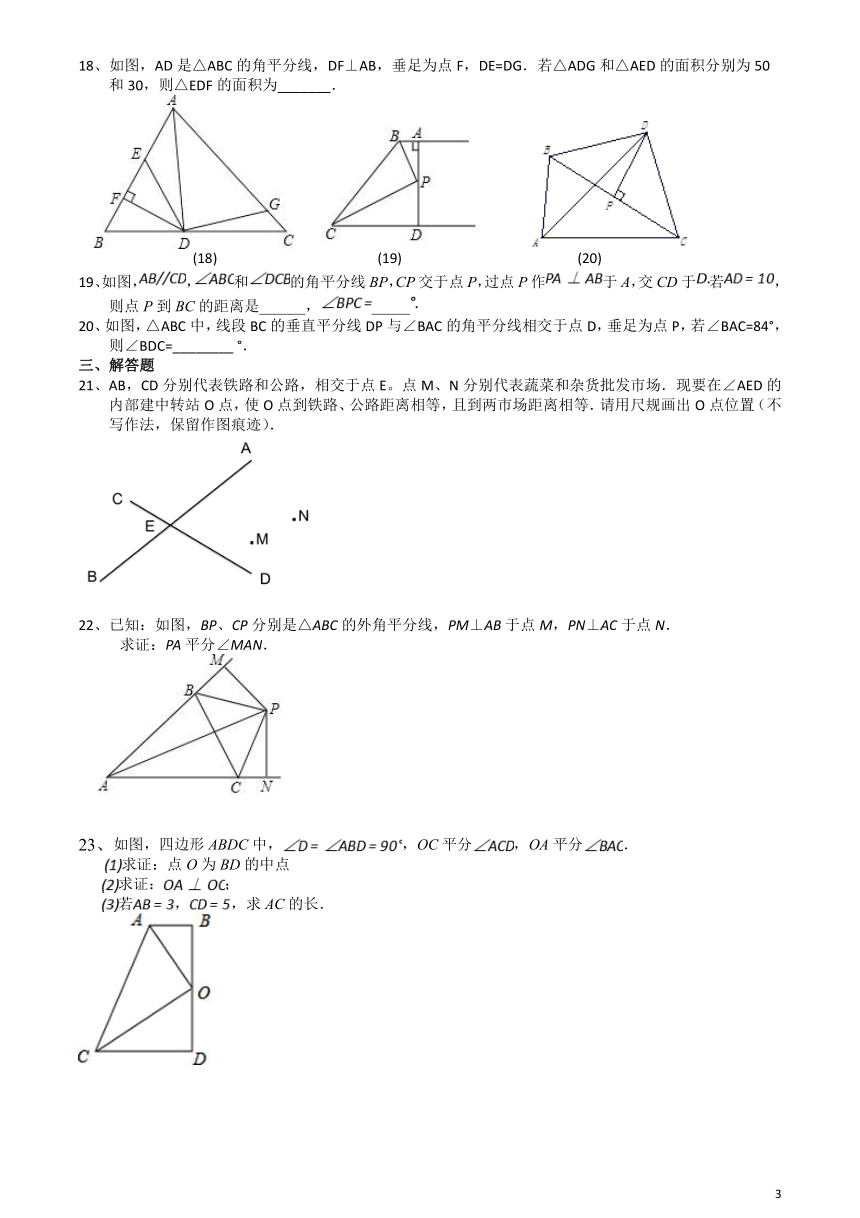
18、如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG.若△ADG和△AED的面积分别为50和30,则△EDF的面积为_______.
(19) (20)
19、如图,,和的角平分线BP,CP交于点P,过点P作于A,交CD于若,则点P到BC的距离是______,_____
20、如图,△ABC中,线段BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC=________?°.
三、解答题
21、AB,CD分别代表铁路和公路,相交于点E。点M、N分别代表蔬菜和杂货批发市场.现要在∠AED的内部建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).
22、已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.
求证:PA平分∠MAN.
如图,四边形ABDC中,,OC平分,OA平分.
求证:点O为BD的中点
求证:;
若,,求AC的长.
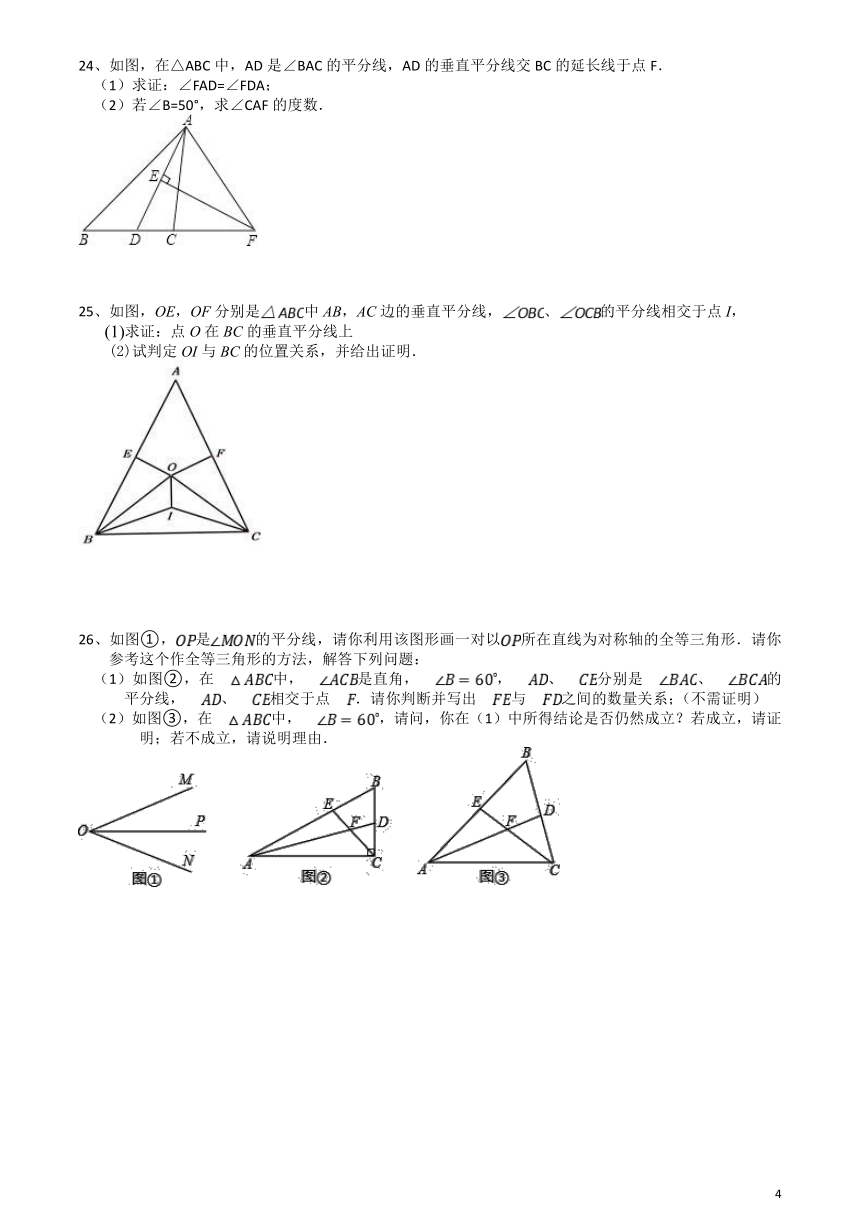
24、如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
25、如图,OE,OF分别是中AB,AC边的垂直平分线,、的平分线相交于点I,
(1)求证:点O在BC的垂直平分线上
(2)试判定OI与BC的位置关系,并给出证明.
26、如图①,是的平分线,请你利用该图形画一对以所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在中,是直角,,、分别是、的平分线,、相交于点.请你判断并写出与之间的数量关系;(不需证明)
(2)如图③,在中,,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
2020-2021苏科版八年级数学上册2.4线段、角的轴对称性专题培优训练卷(答案)
一、选择题
1、如图,DE是中AB边的垂直平分线,厘米,且三角形ACE的周长为16厘米,则的周长为( B )厘米.
A. 16 B. 28 C. 26 D. 18
2、如图,在中,,,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点,作直线MN交BC于点D,连接AD,则的度数为? ? C?
B. C. D.
3、如图,在中,EF是AC的垂直平分线,,,则BC长为(C )
A.13 B. 14 C. 15 D. 16
4、在正方形网格中,△ABC的位置如图所示,且顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是( B )
A.点E B.点F C.点G D.点H
5、如图,在中,边AB、AC的垂直平分线分别交BC于E、若,则周长为? B? ?
A. 12 B. 10 C. 13 D. 无法确定
6、如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=6,DE=3,
则△BCE的面积等于(??B )
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
7、如图,AD是的角平分线,于点E,于点F,,,,
则AC的长是( D )
A. 6 B. 5 C. 4 D. 3
8、如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,
则S△ABO︰S△BCO︰S△CAO 等于( C??)
A.?1︰1︰1????????????????????????????B.?1︰2︰3????????????????????????????C.?2︰3︰4????????????????????????????D.?3︰4︰5
9、如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是(??D )
A.?40°???????????????????????????????????????B.?30°???????????????????????????????????????C.?20°???????????????????????????????????????D.?10°
10、如图,在四边形ABCD中,,,BD平分若点P是BC边上一动点,
则DP长的最小值为( B )
A. 3 B. 4 C. 5 D. 6
二、填空题
11、如图,AD是中的角平分线,于点E,,,,
则AC长是____3_____.
12、如图,在Rt△ABC中,∠C=90°,以点A为圆心,任意长为半径画弧,分别交AC、AB于点M、N , 再分别以M、N为圆心,任意长为半径画弧,两弧交于点O , 作射线AO交BC于点D , 若CD=3,P为AB上一动点,则PD的最小值为___3_____.
13、已知:如图,在中,BD、CE分别平分、,且BD、CE交于点O,过O作于P,于M,于N,则OP、OM、ON的大小关系为_____.
14、如图,在中,,点D,E分别在AC、AB上,BD平分,,,CD=4,
ΔABD的面积为??????30????.
15、如图,中,EF是AB的垂直平分线,与AB交于点D,,,则__12________.
16、如图,线段AB、BC的垂直平分线11、l2相交于点O,若∠1=39°,则∠AOC= 78° .
【解析】过O作射线BP,
∵线段AB、BC的垂直平分线11、l2相交于点O, ∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,∵∠DOE+∠1=180°,∴∠ABC=∠1=39°,
∵OA=OB=OC,∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×39°=78°, 故答案为:78°.
17、如图,AD是△ABC的角平分线,DE⊥AB于E,若AB=18,AC=12,△ABC的面积等于30,则DE= 2 .
18、如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG.若△ADG和△AED的面积分别为50和30,则△EDF的面积为__7.5______.
19、如图,,和的角平分线BP,CP交于点P,过点P作于A,交CD于若,则点P到BC的距离是__5____,___90___
20、如图,△ABC中,线段BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC=___96_____?°.
三、解答题
21、AB,CD分别代表铁路和公路,相交于点E。点M、N分别代表蔬菜和杂货批发市场.现要在∠AED的内部建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).
【答案】 解:点O就是所求的点.
22、已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.
求证:PA平分∠MAN.
【解答】证明:作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC, ∴PM=PD,
同理,PN=PD,∴PM=PN,又PM⊥AB,PN⊥AC, ∴PA平分∠MAN.
23、如图,四边形ABDC中,,OC平分,OA平分.
求证:点O为BD的中点
求证:;
若,,求AC的长.
证明:过点O作于E,如下图所示:
,,
平分,,,
平分,??,,,点O为BD的中点;? ?
,,,,
、OA分别平分、,,
,,;
在和中,,≌,
,同理,得,.
24、如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
【答案】 (1)解:∵AD的垂直平分线交BC的延长线于点F, ∴AF=DF,∴∠FAD=∠FDA
(2)解:∵∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,
∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FAC=∠B=50°.故答案为:50°
25、如图,OE,OF分别是中AB,AC边的垂直平分线,、的平分线相交于点I,
(1)求证:点O在BC的垂直平分线上
(2)试判定OI与BC的位置关系,并给出证明.
解:证明:连接AO,
,OF分别是中AB,AC边的中垂线,,,
,点O在BC的中垂线上;
.
理由:连接OA,过点I作于点M,过点I作于点N,过点I作于点G,
,OF分别是AB,AC边的中垂线,,,,
,的平分线相交于点I,,,,
点I在的角平分线上,.
26、如图①,是的平分线,请你利用该图形画一对以所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在中,是直角,,、分别是、的平分线,、相交于点.请你判断并写出与之间的数量关系;(不需证明)
(2)如图③,在中,,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
答案:(1)FE=FD (2)成立
一、选择题
1、如图,DE是中AB边的垂直平分线,厘米,且三角形ACE的周长为16厘米,则的周长为( )厘米.
A. 16 B. 28 C. 26 D. 18
(2) (3)
2、如图,在中,,,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点,作直线MN交BC于点D,连接AD,则的度数为? ? ?
B. C. D.
3、如图,在中,EF是AC的垂直平分线,,,则BC长为( )
A.13 B. 14 C. 15 D. 16
4、在正方形网格中,△ABC的位置如图所示,且顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是( )
A.点E B.点F C.点G D.点H
(5) (6)
5、如图,在中,边AB、AC的垂直平分线分别交BC于E、若,则周长为? ? ?
A. 12 B. 10 C. 13 D. 无法确定
6、如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=6,DE=3,
则△BCE的面积等于(?? )
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
7、如图,AD是的角平分线,于点E,于点F,,,,
则AC的长是( )
A. 6 B. 5 C. 4 D. 3
(8) (9) (10)
8、如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,
则S△ABO︰S△BCO︰S△CAO 等于( ??)
A.?1︰1︰1????????????????????????????B.?1︰2︰3????????????????????????????C.?2︰3︰4????????????????????????????D.?3︰4︰5
9、如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是(?? )
A.?40°???????????????????????????????????????B.?30°???????????????????????????????????????C.?20°???????????????????????????????????????D.?10°
10、如图,在四边形ABCD中,,,BD平分若点P是BC边上一动点,
则DP长的最小值为( )
A. 3 B. 4 C. 5 D. 6
二、填空题
11、如图,AD是中的角平分线,于点E,,,,
则AC长是________.
12、如图,在Rt△ABC中,∠C=90°,以点A为圆心,任意长为半径画弧,分别交AC、AB于点M、N , 再分别以M、N为圆心,任意长为半径画弧,两弧交于点O , 作射线AO交BC于点D , 若CD=3,P为AB上一动点,则PD的最小值为_______.
13、已知:如图,在中,BD、CE分别平分、,且BD、CE交于点O,过O作于P,于M,于N,则OP、OM、ON的大小关系为__ ___.
14、如图,在中,,点D,E分别在AC、AB上,BD平分,,,CD=4,
ΔABD的面积为??????????.
15、如图,中,EF是AB的垂直平分线,与AB交于点D,,,则________.
16、如图,线段AB、BC的垂直平分线11、l2相交于点O,若∠1=39°,则∠AOC= .
17、如图,AD是△ABC的角平分线,DE⊥AB于E,若AB=18,AC=12,△ABC的面积等于30,则DE= .
18、如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG.若△ADG和△AED的面积分别为50和30,则△EDF的面积为_______.
(19) (20)
19、如图,,和的角平分线BP,CP交于点P,过点P作于A,交CD于若,则点P到BC的距离是______,_____
20、如图,△ABC中,线段BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC=________?°.
三、解答题
21、AB,CD分别代表铁路和公路,相交于点E。点M、N分别代表蔬菜和杂货批发市场.现要在∠AED的内部建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).
22、已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.
求证:PA平分∠MAN.
如图,四边形ABDC中,,OC平分,OA平分.
求证:点O为BD的中点
求证:;
若,,求AC的长.
24、如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
25、如图,OE,OF分别是中AB,AC边的垂直平分线,、的平分线相交于点I,
(1)求证:点O在BC的垂直平分线上
(2)试判定OI与BC的位置关系,并给出证明.
26、如图①,是的平分线,请你利用该图形画一对以所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在中,是直角,,、分别是、的平分线,、相交于点.请你判断并写出与之间的数量关系;(不需证明)
(2)如图③,在中,,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
2020-2021苏科版八年级数学上册2.4线段、角的轴对称性专题培优训练卷(答案)
一、选择题
1、如图,DE是中AB边的垂直平分线,厘米,且三角形ACE的周长为16厘米,则的周长为( B )厘米.
A. 16 B. 28 C. 26 D. 18
2、如图,在中,,,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点,作直线MN交BC于点D,连接AD,则的度数为? ? C?
B. C. D.
3、如图,在中,EF是AC的垂直平分线,,,则BC长为(C )
A.13 B. 14 C. 15 D. 16
4、在正方形网格中,△ABC的位置如图所示,且顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是( B )
A.点E B.点F C.点G D.点H
5、如图,在中,边AB、AC的垂直平分线分别交BC于E、若,则周长为? B? ?
A. 12 B. 10 C. 13 D. 无法确定
6、如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=6,DE=3,
则△BCE的面积等于(??B )
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
7、如图,AD是的角平分线,于点E,于点F,,,,
则AC的长是( D )
A. 6 B. 5 C. 4 D. 3
8、如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,
则S△ABO︰S△BCO︰S△CAO 等于( C??)
A.?1︰1︰1????????????????????????????B.?1︰2︰3????????????????????????????C.?2︰3︰4????????????????????????????D.?3︰4︰5
9、如图,∠A=80°,点O是AB,AC垂直平分线的交点,则∠BCO的度数是(??D )
A.?40°???????????????????????????????????????B.?30°???????????????????????????????????????C.?20°???????????????????????????????????????D.?10°
10、如图,在四边形ABCD中,,,BD平分若点P是BC边上一动点,
则DP长的最小值为( B )
A. 3 B. 4 C. 5 D. 6
二、填空题
11、如图,AD是中的角平分线,于点E,,,,
则AC长是____3_____.
12、如图,在Rt△ABC中,∠C=90°,以点A为圆心,任意长为半径画弧,分别交AC、AB于点M、N , 再分别以M、N为圆心,任意长为半径画弧,两弧交于点O , 作射线AO交BC于点D , 若CD=3,P为AB上一动点,则PD的最小值为___3_____.
13、已知:如图,在中,BD、CE分别平分、,且BD、CE交于点O,过O作于P,于M,于N,则OP、OM、ON的大小关系为_____.
14、如图,在中,,点D,E分别在AC、AB上,BD平分,,,CD=4,
ΔABD的面积为??????30????.
15、如图,中,EF是AB的垂直平分线,与AB交于点D,,,则__12________.
16、如图,线段AB、BC的垂直平分线11、l2相交于点O,若∠1=39°,则∠AOC= 78° .
【解析】过O作射线BP,
∵线段AB、BC的垂直平分线11、l2相交于点O, ∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,∵∠DOE+∠1=180°,∴∠ABC=∠1=39°,
∵OA=OB=OC,∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×39°=78°, 故答案为:78°.
17、如图,AD是△ABC的角平分线,DE⊥AB于E,若AB=18,AC=12,△ABC的面积等于30,则DE= 2 .
18、如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG.若△ADG和△AED的面积分别为50和30,则△EDF的面积为__7.5______.
19、如图,,和的角平分线BP,CP交于点P,过点P作于A,交CD于若,则点P到BC的距离是__5____,___90___
20、如图,△ABC中,线段BC的垂直平分线DP与∠BAC的角平分线相交于点D,垂足为点P,若∠BAC=84°,则∠BDC=___96_____?°.
三、解答题
21、AB,CD分别代表铁路和公路,相交于点E。点M、N分别代表蔬菜和杂货批发市场.现要在∠AED的内部建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置(不写作法,保留作图痕迹).
【答案】 解:点O就是所求的点.
22、已知:如图,BP、CP分别是△ABC的外角平分线,PM⊥AB于点M,PN⊥AC于点N.
求证:PA平分∠MAN.
【解答】证明:作PD⊥BC于点D,
∵BP是△ABC的外角平分线,PM⊥AB,PD⊥BC, ∴PM=PD,
同理,PN=PD,∴PM=PN,又PM⊥AB,PN⊥AC, ∴PA平分∠MAN.
23、如图,四边形ABDC中,,OC平分,OA平分.
求证:点O为BD的中点
求证:;
若,,求AC的长.
证明:过点O作于E,如下图所示:
,,
平分,,,
平分,??,,,点O为BD的中点;? ?
,,,,
、OA分别平分、,,
,,;
在和中,,≌,
,同理,得,.
24、如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
【答案】 (1)解:∵AD的垂直平分线交BC的延长线于点F, ∴AF=DF,∴∠FAD=∠FDA
(2)解:∵∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,
∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FAC=∠B=50°.故答案为:50°
25、如图,OE,OF分别是中AB,AC边的垂直平分线,、的平分线相交于点I,
(1)求证:点O在BC的垂直平分线上
(2)试判定OI与BC的位置关系,并给出证明.
解:证明:连接AO,
,OF分别是中AB,AC边的中垂线,,,
,点O在BC的中垂线上;
.
理由:连接OA,过点I作于点M,过点I作于点N,过点I作于点G,
,OF分别是AB,AC边的中垂线,,,,
,的平分线相交于点I,,,,
点I在的角平分线上,.
26、如图①,是的平分线,请你利用该图形画一对以所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在中,是直角,,、分别是、的平分线,、相交于点.请你判断并写出与之间的数量关系;(不需证明)
(2)如图③,在中,,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
答案:(1)FE=FD (2)成立
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
