三角形全等的判定SAS
图片预览


文档简介
(共13张PPT)
三角形全等的判定
只为成功找方法;不为失败找理由!
知识回顾
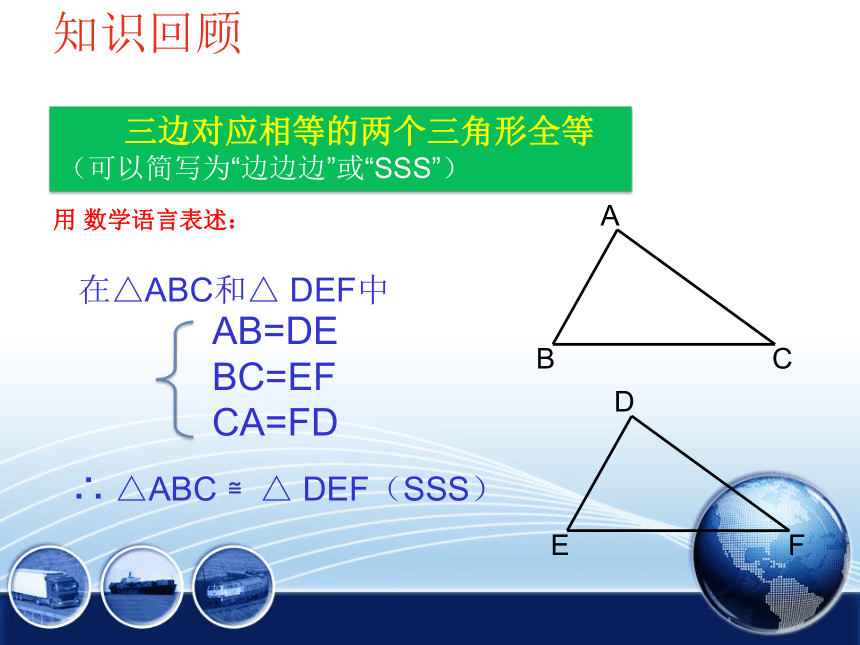
三边对应相等的两个三角形全等
(可以简写为“边边边”或“SSS”)
A
B
C
D
E
F
用 数学语言表述:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
满足下列条件的两个三角形是一定否全等:
一个条件
两个条件
三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
√
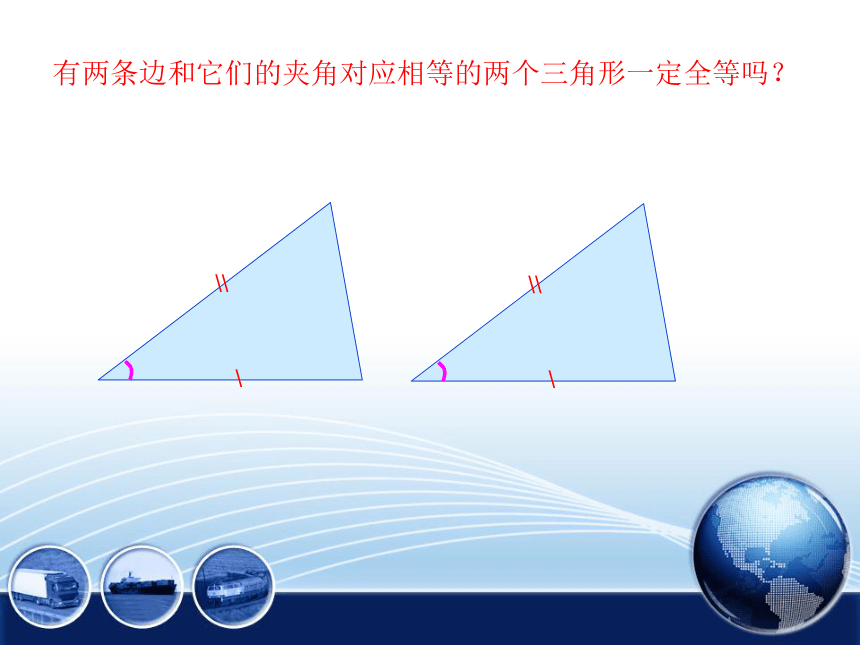
有两条边和它们的夹角对应相等的两个三角形一定全等吗?
\\
\
\\
\
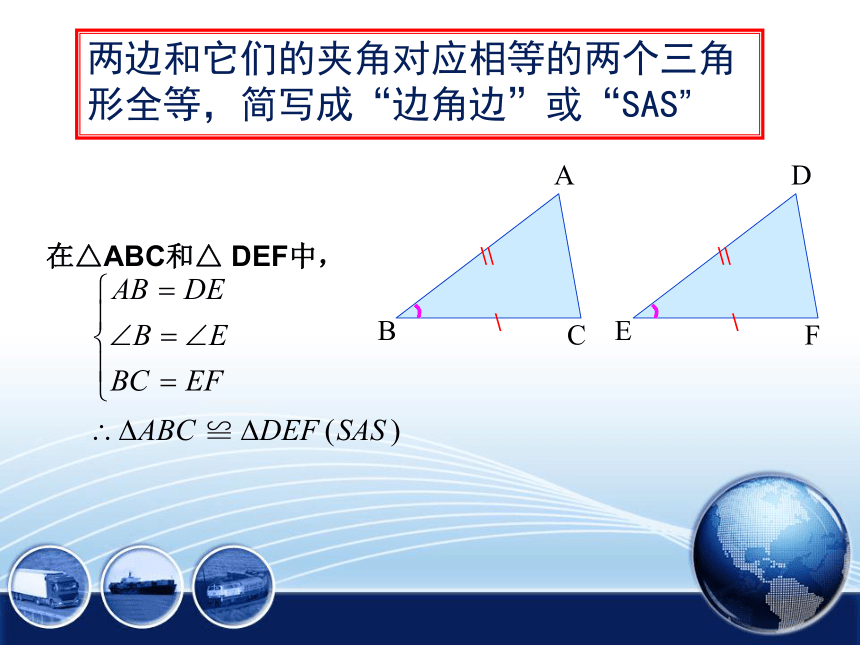
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△ DEF中,
A
B
C
45°
1.5
3
45°
3
1.5
P
M
N
60°
D
E
F
3
1.5
③
①
②
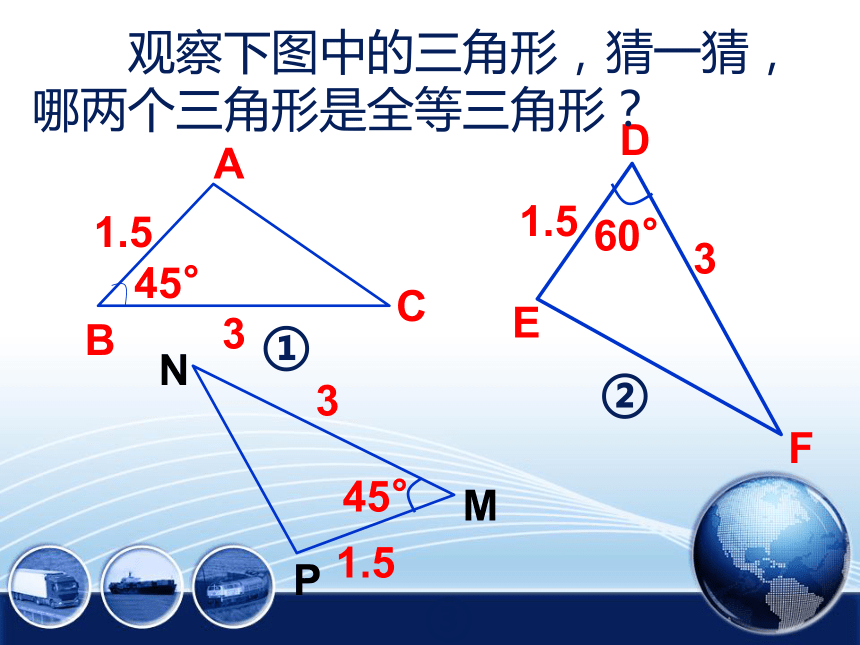
观察下图中的三角形,猜一猜,
哪两个三角形是全等三角形?
例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
分析:如果能证明△ABC≌△DEC ,就可以得出AB=DE.
在△ABC和△DEC中,CA=CD , CB=CE .如果能得出∠ACB=∠DCE, △ABC和△DEC就全等了
已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?
A
B
C
D
例题推广
证明:在△ABD与△CBD中
∴△ABD≌△CBD(SAS)
∴AD=CD
∠ADB=∠CDB
即BD平分∠ADC
AB=CB
∠ABD=∠CBD
BD=BD
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。
由前边两个题目可以看出:
探究
两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
已知:如图,AD∥BC,AD=CB. 求证:AB=CD.
【提示】连结AC,
由 △ABC≌△CDA
故 AB=CD.
例题拓广
课堂小结:
2. 用尺规作图:已知两边及其夹角的三角形
1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)
课本15页3、4题
布置作业:
三角形全等的判定
只为成功找方法;不为失败找理由!
知识回顾
三边对应相等的两个三角形全等
(可以简写为“边边边”或“SSS”)
A
B
C
D
E
F
用 数学语言表述:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
满足下列条件的两个三角形是一定否全等:
一个条件
两个条件
三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
√
有两条边和它们的夹角对应相等的两个三角形一定全等吗?
\\
\
\\
\
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△ DEF中,
A
B
C
45°
1.5
3
45°
3
1.5
P
M
N
60°
D
E
F
3
1.5
③
①
②
观察下图中的三角形,猜一猜,
哪两个三角形是全等三角形?
例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
分析:如果能证明△ABC≌△DEC ,就可以得出AB=DE.
在△ABC和△DEC中,CA=CD , CB=CE .如果能得出∠ACB=∠DCE, △ABC和△DEC就全等了
已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?
A
B
C
D
例题推广
证明:在△ABD与△CBD中
∴△ABD≌△CBD(SAS)
∴AD=CD
∠ADB=∠CDB
即BD平分∠ADC
AB=CB
∠ABD=∠CBD
BD=BD
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。
由前边两个题目可以看出:
探究
两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?
已知:如图,AD∥BC,AD=CB. 求证:AB=CD.
【提示】连结AC,
由 △ABC≌△CDA
故 AB=CD.
例题拓广
课堂小结:
2. 用尺规作图:已知两边及其夹角的三角形
1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)
课本15页3、4题
布置作业:
