全等三角形的判定(ASA)
图片预览


文档简介
(共16张PPT)
三角形全等的条件
新人教版 八年级数学
台前县第一初级中学
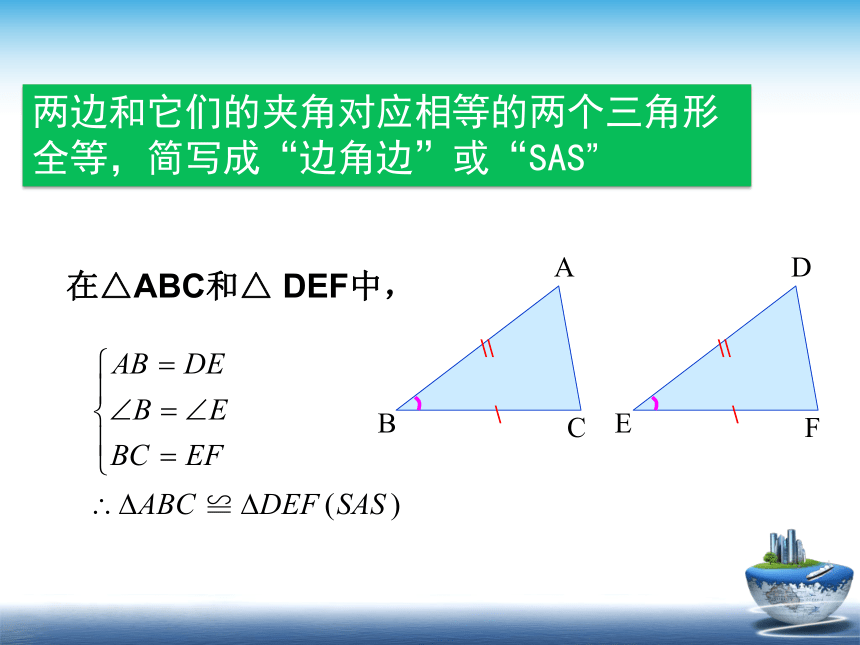
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△ DEF中,
满足下列条件的两个三角形是一定否全等:
一个条件
两个条件
三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
√
√
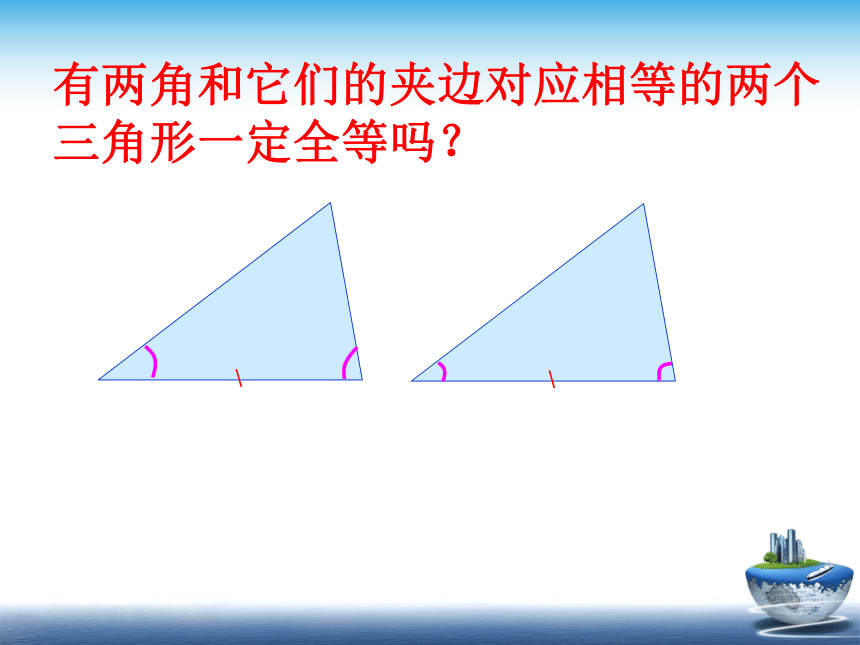
有两角和它们的夹边对应相等的两个三角形一定全等吗?
\
\
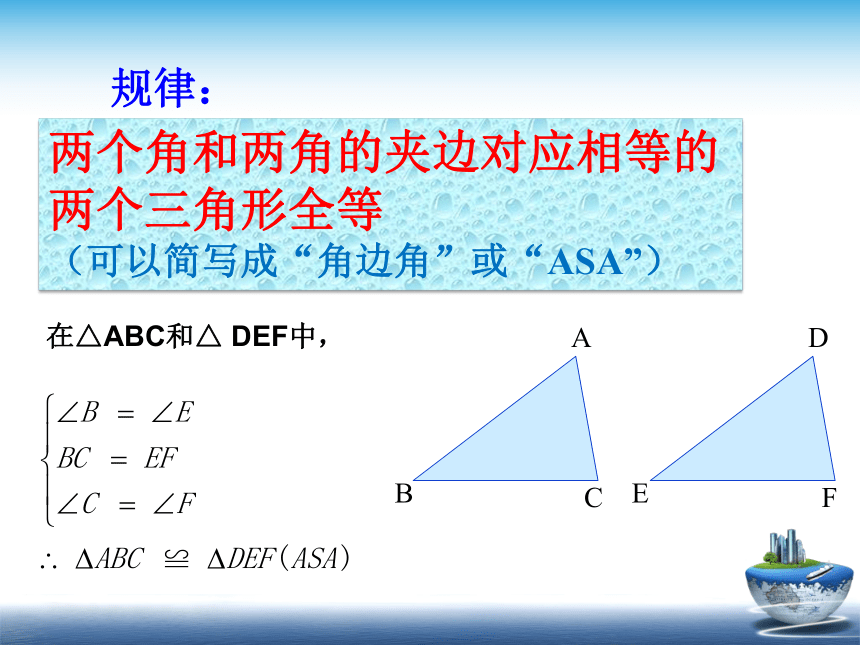
规律:
两个角和两角的夹边对应相等的两个三角形全等
(可以简写成“角边角”或“ASA”)
A
B
C
D
E
F
在△ABC和△ DEF中,
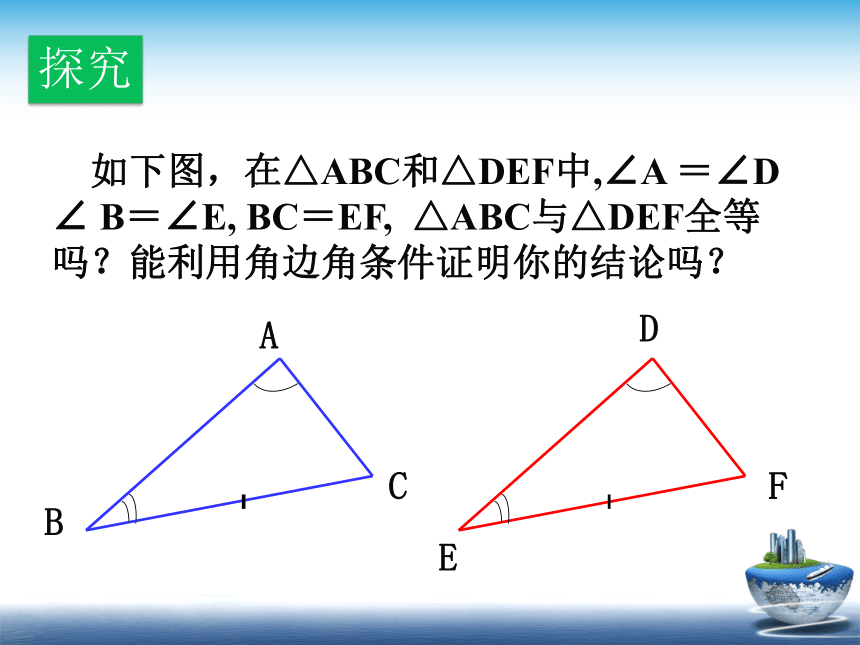
探究
如下图,在△ABC和△DEF中,∠A =∠D ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
B
A
C
E
F
D
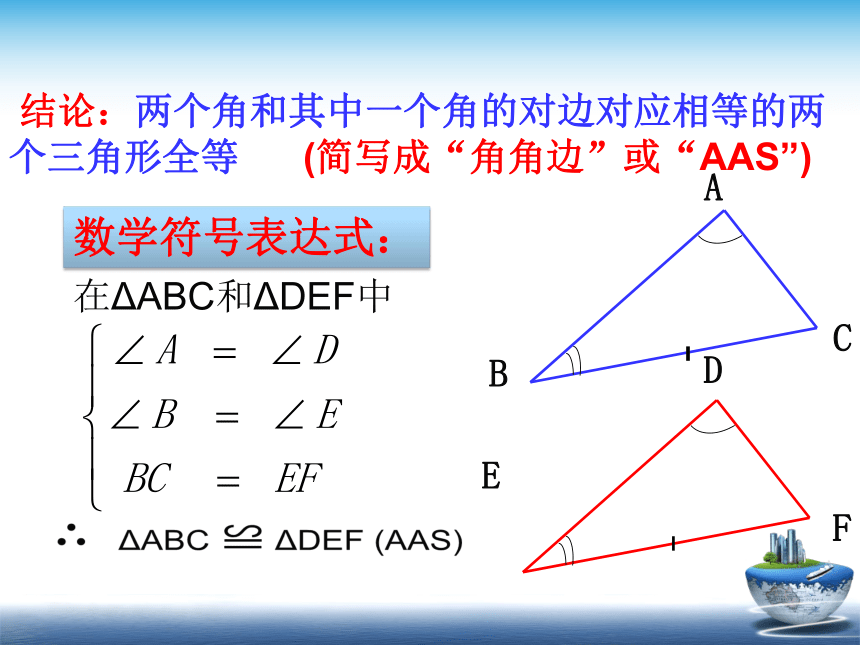
结论:两个角和其中一个角的对边对应相等的两个三角形全等 (简写成“角角边”或“AAS”)
E
F
D
B
A
C
数学符号表达式:
在ΔABC和ΔDEF中
ΔABC ≌ ΔDEF (AAS)
例3:已知,如图,D在AB上,E在AC上,AB=AC,∠B=∠C,求证:AD=AE
证明:在△ACD和△ABE中,
∠A=∠A(公共角)
AC=AB (已知)
∠C= ∠B(已知)
∴ △ACD≌ △ABE(ASA)
∴ AD=AE
1、已知:如图,∠1= ∠2, ∠3 = ∠4。
求证: AC=AD。
1
2
3
4
A
B
C
D
应用练习
1、如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD
证明:∵AB⊥BC,AD⊥DC(已知)
∴ ∠B=∠D=900
在⊿ABC和⊿ADC中
∠1=∠2
∠B=∠D
AC=AC(公共边)
∴⊿ABC≌⊿ADC(AAS)
∴ AB=AD
应用练习
2、如图,已知:AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C,求证:AE=CF
证明:∵ AB∥CD (已知)
∴ ∠B=∠D(两直线平行,内错角相等)
在⊿ABE和⊿CDF中
∠B=∠D(已证)
AB=CD(已知)
∠A=∠C (已知)
∴⊿ABE≌⊿CDF(ASA)
∴ AB=AD
能力提高练习
如图:已知△ABC≌△A1B1C1,AD、A1D1分别是∠BAC和∠B1 A1 C1的角平分线。求证:AD= A1D1
证明:∵ △ABC≌△A1B1C1
∴AB=A1B1,∠B=∠B1, ∠BAC=∠B1A1C1
(全等三角形的性质)
又∵ AD、A1D1分别是∠BAC和∠B1 A1 C1的角平分线
∴∠BAD=∠B1A1C1
在在⊿BAD和⊿B1A1D1中
∠B=∠B1
AB=A1B1
∠BAD=∠B1A1C1
∴ ⊿BAD≌⊿B1A1D1(ASA)
∴ AD= A1D1
(1)学习了ASA和AAS。
(2)由实践证明角边角是真命题。
(3)要根据题意选择适当的方法。
(4)证明线段或角相等,就是证明
它们所在的两个三角形全等。
小结
知识应用
1.如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?
A
B
C
D
E
F
应用练习
1、如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD
证明:∵AB⊥BC,AD⊥DC(已知)
∴ ∠B=∠D=900
在⊿ABC和⊿ADC中
∠1=∠2
∠B=∠D
AC=AC(公共边)
∴⊿ABC≌⊿ADC(AAS)
∴ AB=AD
问题情境
一同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店做一块与原玻璃一模一样的?
三角形全等的条件
新人教版 八年级数学
台前县第一初级中学
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
\\
\
A
B
C
\\
\
D
E
F
在△ABC和△ DEF中,
满足下列条件的两个三角形是一定否全等:
一个条件
两个条件
三个条件
一边
一角
两边
一边一角
两角
三角
三边
两边一角
两角一边
×
×
只有一个条件对应相等的两个三角形不一定全等。
×
×
×
只有两个条件对应相等的两个三角形不一定全等。
×
√
√
有两角和它们的夹边对应相等的两个三角形一定全等吗?
\
\
规律:
两个角和两角的夹边对应相等的两个三角形全等
(可以简写成“角边角”或“ASA”)
A
B
C
D
E
F
在△ABC和△ DEF中,
探究
如下图,在△ABC和△DEF中,∠A =∠D ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
B
A
C
E
F
D
结论:两个角和其中一个角的对边对应相等的两个三角形全等 (简写成“角角边”或“AAS”)
E
F
D
B
A
C
数学符号表达式:
在ΔABC和ΔDEF中
ΔABC ≌ ΔDEF (AAS)
例3:已知,如图,D在AB上,E在AC上,AB=AC,∠B=∠C,求证:AD=AE
证明:在△ACD和△ABE中,
∠A=∠A(公共角)
AC=AB (已知)
∠C= ∠B(已知)
∴ △ACD≌ △ABE(ASA)
∴ AD=AE
1、已知:如图,∠1= ∠2, ∠3 = ∠4。
求证: AC=AD。
1
2
3
4
A
B
C
D
应用练习
1、如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD
证明:∵AB⊥BC,AD⊥DC(已知)
∴ ∠B=∠D=900
在⊿ABC和⊿ADC中
∠1=∠2
∠B=∠D
AC=AC(公共边)
∴⊿ABC≌⊿ADC(AAS)
∴ AB=AD
应用练习
2、如图,已知:AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C,求证:AE=CF
证明:∵ AB∥CD (已知)
∴ ∠B=∠D(两直线平行,内错角相等)
在⊿ABE和⊿CDF中
∠B=∠D(已证)
AB=CD(已知)
∠A=∠C (已知)
∴⊿ABE≌⊿CDF(ASA)
∴ AB=AD
能力提高练习
如图:已知△ABC≌△A1B1C1,AD、A1D1分别是∠BAC和∠B1 A1 C1的角平分线。求证:AD= A1D1
证明:∵ △ABC≌△A1B1C1
∴AB=A1B1,∠B=∠B1, ∠BAC=∠B1A1C1
(全等三角形的性质)
又∵ AD、A1D1分别是∠BAC和∠B1 A1 C1的角平分线
∴∠BAD=∠B1A1C1
在在⊿BAD和⊿B1A1D1中
∠B=∠B1
AB=A1B1
∠BAD=∠B1A1C1
∴ ⊿BAD≌⊿B1A1D1(ASA)
∴ AD= A1D1
(1)学习了ASA和AAS。
(2)由实践证明角边角是真命题。
(3)要根据题意选择适当的方法。
(4)证明线段或角相等,就是证明
它们所在的两个三角形全等。
小结
知识应用
1.如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?
A
B
C
D
E
F
应用练习
1、如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD
证明:∵AB⊥BC,AD⊥DC(已知)
∴ ∠B=∠D=900
在⊿ABC和⊿ADC中
∠1=∠2
∠B=∠D
AC=AC(公共边)
∴⊿ABC≌⊿ADC(AAS)
∴ AB=AD
问题情境
一同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店做一块与原玻璃一模一样的?
