2011-2012学年高一物理必修1(人教版)课件第二章 匀变速直线运动的研究2.3 匀变速直线运动的位移与时间的关系
文档属性
| 名称 | 2011-2012学年高一物理必修1(人教版)课件第二章 匀变速直线运动的研究2.3 匀变速直线运动的位移与时间的关系 |  | |
| 格式 | rar | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-09-12 15:49:41 | ||
图片预览






文档简介
(共17张PPT)
第二章 匀变速直线运动的研究
学案3 匀变速直线运动的位移与时间的关系
驾驶员都知道车辆在行驶中保持一定的距离很重要。因为一旦遇到险情,车辆制动后还要向前滑行一段距离,更何况驾驶员作出制动反应还要有一定的时间呢!据公安部门规定,上海市区交通繁忙路段机动车辆的速度限制在25 km/h以内,并要求驾驶员必须保持至少5 m的车距。一旦发生交通事故,我们会看到交警同志测量有关距离,其中非常重要的是刹车距离。你知道测量刹车距离的目的吗?这样做的物理原理是什么?
学点1 匀速直线运动的位移
匀速直线运动中,速度的大小和方向不随时间变化,我们以横轴表示时间,纵轴表示速度,在平面直角坐标系中就可作出匀速直线运动的v-t图象。如图2-2-3所示,它的图象是一条平行于时间轴的直线。
匀速运动中x=vt。因此位移等于对应时间间隔内的图线与t轴所包围的“面积”,如图在t0时间内的位移x=v0t0。它在数值上等于“阴影”的面积。位移也有正、负,若包围的“面积”在第一象限,则为正;若在第四象限,则为负。
图2-2-3
学点2 匀变速直线运动的位移
图2-3-2
图2-3-3
【例1】若一质点从t=0开始由原点出发沿直线运动,
其速度—时间图象如图2-3-3所示,则该质点
( )
A.t=1 s时离原点最近
B.t=2 s时离原点最远
C.t=3 s时回到原点
D.t=3 s时回到原点,路程为10 m
BD
图2-3-3
1
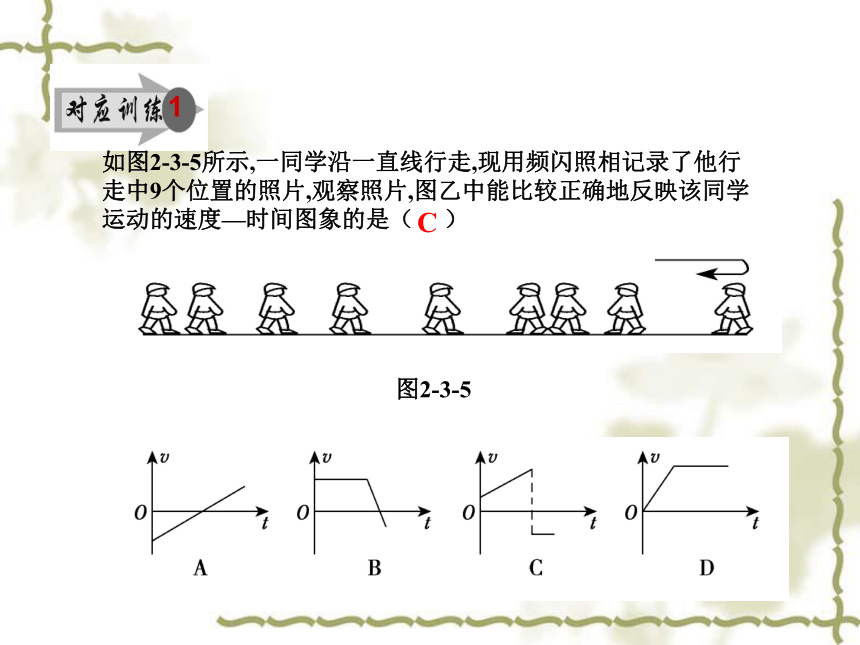
如图2-3-5所示,一同学沿一直线行走,现用频闪照相记录了他行走中9个位置的照片,观察照片,图乙中能比较正确地反映该同学运动的速度—时间图象的是( )
C
图2-3-5
【例2】一艘快艇以2 m/s2的加速度在海面上做匀加速直线运动,
快艇的初速度是6 m/s。求:
(1)这艘快艇在8 s末的速度和8 s内的位移;
(2)快艇在第8 s内的位移。
【答案】(1)22 m/s 112 m(2)21 m
【解析】快艇在第8 s末的速度为
v=v0+at1=6 m/s+2×8 m/s=22 m/s
快艇在前8 s内的位移为
x1=v0t1+1/2at21=6×8 m
+1/2×2×82 m=112 m
(2)快艇在第8 s内的初速度即为第7 s末的速度
v2=v0+at2=6 m/s+2×7 m/s=20 m/s
快艇在第8 s内的位移为
x2=v2t3+1/2at23=20×1 m
+1/2×2×12 m=21 m。
【评析】应用v=v0+at和x=v0t+1/2at2求解问题时,必须明确所研究的过程,进而明确其对应的时间、初速度、末速度和加速度。
2
钢球在斜槽上做初速度为零的匀加速直线运动。开始运动后0.2 s内通过的位移是3 cm,则它在第1 s内的位移是_________m。如果斜面长1.5 m,钢球从静止开始由斜面顶端滚到底端需要的时间是________s。
0.75
【例3】以10 m/s的速度匀速行驶的汽车,刹车后做匀减速直线运动。
若汽车刹车后第2s内的位移为6.25m(刹车时间超过2s),则刹车
后6s内汽车的位移是多大?
【答案】20 m
3
骑自行车的人以5 m/s的初速度匀减速地上一个斜坡,加速度的大小为0.4 m/s2,斜坡长30 m,骑自行车的人通过斜坡需要多少时间?
【答案】10 s
学点3 用图象表示位移
(1)位移图象的意义
表示物体离开t=0时刻所处位置的位移随时间变化的规律,在图2-3-4中坐标点(t1,x1)表示t1时刻物体离开初位置(t=0)的位移为x1,在t1~t2时间内的位移为Δx=x2-x1。
图2-3-4
(2)速度在x-t图象中的体现
在x-t图象中,任意一点处的切线斜率表示该时刻物体的速度。在图2-3-4中,t1、t2两时刻的速度v1、v2满足v1【例4】一质点做直线运动的位移时间图象如图2-3-5所示,试回
答以下问题。
(1)0~2 s和2 s~4 s内质点做什么运动?
(2)在0~2 s内、0~4 s内和2~4 s内的位
移分别为多少?
【答案】(1)0~2 s内物体做匀速运动,且速度v=5 m/s 在2~4 s内物体静止不动
(2)10 m, 10 m, 0
图2-3-5
【解析】(1)在0~2 s内,x-t图象为倾斜直线;表示物体做匀速直线运动,速度v=Δx/t=10/2 m/s=5 m/s
在2~4 s内物体始终处于x=10 m处不动。
(2)在0~2 s内位移为Δx1=10 m;
在0~4 s内位移为Δx2=10 m;
在2~4 s内位移为Δx3=0。
4
试画出按v=2+2t m/s规律匀加速运动的位移图象。
如图
1.位移公式x=v0t+1/2at2是通过匀加速直线运动的v-t图象中图线与坐标轴之间的面积求得的,它适用于匀减速运动吗?
根据x=v0t+1/2at2的推导过程可以看出,公式对匀减速运动同样适用。只是注意:这一位移公式是矢量式,以v0的方向为正方向,对匀加速直线运动,a为正;对匀减速直线运动,a为负。
2.既然匀变速直线运动v-t图线下面的面积等于它的位移,那么能否据此求出匀变速直线运动的平均速度的表达式?
如图所示,质点以初速度v0做匀变速运动,它的位移等于梯形Ot1Av0所包围的面积。由图知,以速度v末/2做匀速直线运动的位移等于以速度v末/2匀速运动的图线下面矩形的面积。图中的两个三角形面积(阴影部分)是相等的,由此得出结论:匀变速直线运动的平均速度,等于初末两个时刻速度的平均值,即v=(v0+v末)/2。
退出
第二章 匀变速直线运动的研究
学案3 匀变速直线运动的位移与时间的关系
驾驶员都知道车辆在行驶中保持一定的距离很重要。因为一旦遇到险情,车辆制动后还要向前滑行一段距离,更何况驾驶员作出制动反应还要有一定的时间呢!据公安部门规定,上海市区交通繁忙路段机动车辆的速度限制在25 km/h以内,并要求驾驶员必须保持至少5 m的车距。一旦发生交通事故,我们会看到交警同志测量有关距离,其中非常重要的是刹车距离。你知道测量刹车距离的目的吗?这样做的物理原理是什么?
学点1 匀速直线运动的位移
匀速直线运动中,速度的大小和方向不随时间变化,我们以横轴表示时间,纵轴表示速度,在平面直角坐标系中就可作出匀速直线运动的v-t图象。如图2-2-3所示,它的图象是一条平行于时间轴的直线。
匀速运动中x=vt。因此位移等于对应时间间隔内的图线与t轴所包围的“面积”,如图在t0时间内的位移x=v0t0。它在数值上等于“阴影”的面积。位移也有正、负,若包围的“面积”在第一象限,则为正;若在第四象限,则为负。
图2-2-3
学点2 匀变速直线运动的位移
图2-3-2
图2-3-3
【例1】若一质点从t=0开始由原点出发沿直线运动,
其速度—时间图象如图2-3-3所示,则该质点
( )
A.t=1 s时离原点最近
B.t=2 s时离原点最远
C.t=3 s时回到原点
D.t=3 s时回到原点,路程为10 m
BD
图2-3-3
1
如图2-3-5所示,一同学沿一直线行走,现用频闪照相记录了他行走中9个位置的照片,观察照片,图乙中能比较正确地反映该同学运动的速度—时间图象的是( )
C
图2-3-5
【例2】一艘快艇以2 m/s2的加速度在海面上做匀加速直线运动,
快艇的初速度是6 m/s。求:
(1)这艘快艇在8 s末的速度和8 s内的位移;
(2)快艇在第8 s内的位移。
【答案】(1)22 m/s 112 m(2)21 m
【解析】快艇在第8 s末的速度为
v=v0+at1=6 m/s+2×8 m/s=22 m/s
快艇在前8 s内的位移为
x1=v0t1+1/2at21=6×8 m
+1/2×2×82 m=112 m
(2)快艇在第8 s内的初速度即为第7 s末的速度
v2=v0+at2=6 m/s+2×7 m/s=20 m/s
快艇在第8 s内的位移为
x2=v2t3+1/2at23=20×1 m
+1/2×2×12 m=21 m。
【评析】应用v=v0+at和x=v0t+1/2at2求解问题时,必须明确所研究的过程,进而明确其对应的时间、初速度、末速度和加速度。
2
钢球在斜槽上做初速度为零的匀加速直线运动。开始运动后0.2 s内通过的位移是3 cm,则它在第1 s内的位移是_________m。如果斜面长1.5 m,钢球从静止开始由斜面顶端滚到底端需要的时间是________s。
0.75
【例3】以10 m/s的速度匀速行驶的汽车,刹车后做匀减速直线运动。
若汽车刹车后第2s内的位移为6.25m(刹车时间超过2s),则刹车
后6s内汽车的位移是多大?
【答案】20 m
3
骑自行车的人以5 m/s的初速度匀减速地上一个斜坡,加速度的大小为0.4 m/s2,斜坡长30 m,骑自行车的人通过斜坡需要多少时间?
【答案】10 s
学点3 用图象表示位移
(1)位移图象的意义
表示物体离开t=0时刻所处位置的位移随时间变化的规律,在图2-3-4中坐标点(t1,x1)表示t1时刻物体离开初位置(t=0)的位移为x1,在t1~t2时间内的位移为Δx=x2-x1。
图2-3-4
(2)速度在x-t图象中的体现
在x-t图象中,任意一点处的切线斜率表示该时刻物体的速度。在图2-3-4中,t1、t2两时刻的速度v1、v2满足v1
答以下问题。
(1)0~2 s和2 s~4 s内质点做什么运动?
(2)在0~2 s内、0~4 s内和2~4 s内的位
移分别为多少?
【答案】(1)0~2 s内物体做匀速运动,且速度v=5 m/s 在2~4 s内物体静止不动
(2)10 m, 10 m, 0
图2-3-5
【解析】(1)在0~2 s内,x-t图象为倾斜直线;表示物体做匀速直线运动,速度v=Δx/t=10/2 m/s=5 m/s
在2~4 s内物体始终处于x=10 m处不动。
(2)在0~2 s内位移为Δx1=10 m;
在0~4 s内位移为Δx2=10 m;
在2~4 s内位移为Δx3=0。
4
试画出按v=2+2t m/s规律匀加速运动的位移图象。
如图
1.位移公式x=v0t+1/2at2是通过匀加速直线运动的v-t图象中图线与坐标轴之间的面积求得的,它适用于匀减速运动吗?
根据x=v0t+1/2at2的推导过程可以看出,公式对匀减速运动同样适用。只是注意:这一位移公式是矢量式,以v0的方向为正方向,对匀加速直线运动,a为正;对匀减速直线运动,a为负。
2.既然匀变速直线运动v-t图线下面的面积等于它的位移,那么能否据此求出匀变速直线运动的平均速度的表达式?
如图所示,质点以初速度v0做匀变速运动,它的位移等于梯形Ot1Av0所包围的面积。由图知,以速度v末/2做匀速直线运动的位移等于以速度v末/2匀速运动的图线下面矩形的面积。图中的两个三角形面积(阴影部分)是相等的,由此得出结论:匀变速直线运动的平均速度,等于初末两个时刻速度的平均值,即v=(v0+v末)/2。
退出
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
