2011-2012学年高一物理必修1(人教版)学案课件第三章 相互作用3.4 力的合成
文档属性
| 名称 | 2011-2012学年高一物理必修1(人教版)学案课件第三章 相互作用3.4 力的合成 |

|
|
| 格式 | rar | ||
| 文件大小 | 728.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-09-12 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
第三章 相互作用
学案4 力的合成
一首优美动听的《清江放排》勾勒出了一幅放排工艰辛劳动的情景,在逆水行舟时,放排工在岸上背驼缆绳,唱着响亮的劳动号子,将竹排在逆水中向前缓慢拉动,如图所示。
你能从力学的角度上解释它的道理吗?
假设有机动船的话,就不要人拉了。机
械推力就可以使船逆水而上,但在没有机械
动力的情形下,两岸的拉力F1、F2可以产生与机械动力相同的效果——也能使船逆水而上。
学点1 力的合成
⑴合力与分力
①定义:一个力产生的效果跟几个力的共同作用产生的效果相同,则这个力就叫那几个力的合力,那几个力叫做分力。
②两点诠释合力与分力的关系。
a.合力与分力是一种等效替代的关系,即分力与合力虽然不同时作用在物体上,但可以相互替代,能够相互替代的条件是分力和合力的作用效果相同,但不能同时考虑分力的作用与合力的作用。
b.两个力的作用效果可以用一个力替代,进一步想,满足一定条件的多个力的作用效果也可由一个力来替代。
⑵力的合成
①定义:求几个力的合力的过程叫做力的合成。
②说明:力的合成的实质是找一个力去替代作用在物体上的几个已知的力,而不改变其作用效果的方法。
(3)探究力的合成的法则
实验装置如图3-4-1所示。
探究过程:①在长木板上用图钉固定一张白纸,在白纸上用图
钉固定一个橡皮筋;
②在橡皮筋的另一端拴上两个细绳套,用两个弹簧测力计互成
角度地拉橡皮筋,记下结点的位置O,弹簧测力计的示数和细绳套
的方向,即两分力F1、F2的大小和方向;
③再用一个弹簧测力计拉细绳套,拉到结点位置O,记下此时
的力F的大小和方向;
④选定标度,作出力F1、F2、F的图示;
⑤以F1、F2为邻边作平行四边形,并作出对角线,如图3-4
-2所示。
实验结论:F和对角线F′在误差范围内重合,说明两个力合成
时,用表示这两个力的线段为邻边作平行四边形,则平行四边形的对
角线所代表的力与合力的大小和方向是相同的。
注意事项:①在使用弹簧测力计拉细绳套时,要使测力计的弹簧
与细绳套在同一直线上,弹簧与木板面平行,避免弹簧与测力计壳有
摩擦;
②作力的图示时,标度要统一。
图3-4-1
图3-4-2
(4)平行四边形定则
①内容:两个力合成时,以表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向,这个法则叫做平行四边形定则。
说明:平行四边形定则是矢量运算的基本法则。
②应用平行四边形定则求合力的三点注意
a.力的标度要适当
b.虚线、实线要分清,表示分力和合力的两条邻边和对角线画实线,并加上箭头,平行四边形的另两条边画虚线;
c.求合力时既要求出合力的大小,还要求出合力的方向,不要忘了用量角器量出合力与某一分力间的夹角。
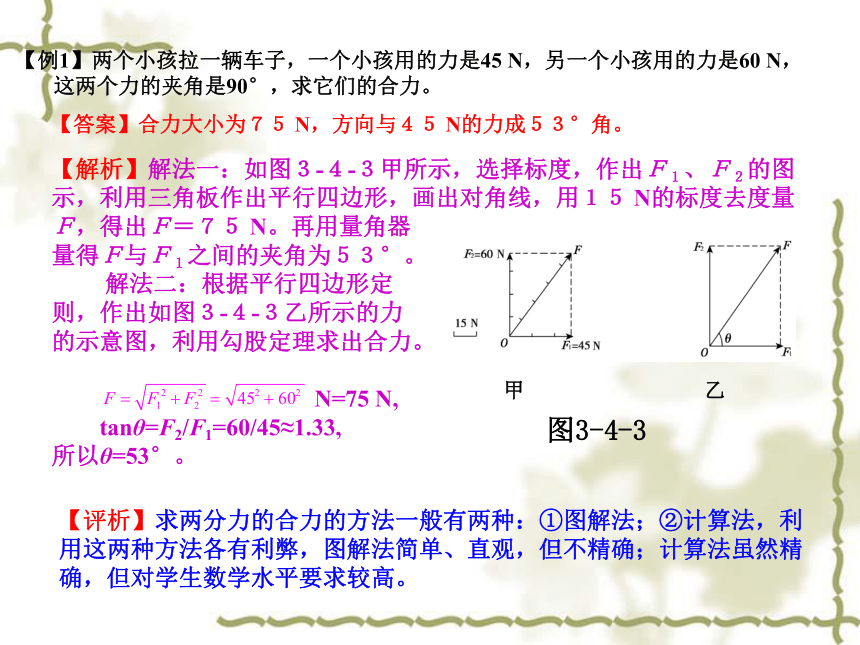
【例1】两个小孩拉一辆车子,一个小孩用的力是45 N,另一个小孩用的力是60 N,
这两个力的夹角是90°,求它们的合力。
【答案】合力大小为75 N,方向与45 N的力成53°角。
【解析】解法一:如图3-4-3甲所示,选择标度,作出F1、F2的图示,利用三角板作出平行四边形,画出对角线,用15 N的标度去度量F,得出F=75 N。再用量角器
量得F与F1之间的夹角为53°。
解法二:根据平行四边形定
则,作出如图3-4-3乙所示的力
的示意图,利用勾股定理求出合力。
N=75 N,
tanθ=F2/F1=60/45≈1.33,
所以θ=53°。
甲 乙
图3-4-3
【评析】求两分力的合力的方法一般有两种:①图解法;②计算法,利用这两种方法各有利弊,图解法简单、直观,但不精确;计算法虽然精确,但对学生数学水平要求较高。
1
如图3-4-4所示,为使电线杆稳定,在杆上加了两根拉线CA和CB,若每根拉线的拉力都是330 N,两根拉线间的夹角为60°角.求拉线拉力的合力大小和方向.
【答案】520 N 向竖直向下
图3-4-4
⑶多个力合成的方法
如果有两个以上共点力作用在物体上,我们也可以应用平行四边形定则求出它们的合力:先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。
说明:①平行四边形定则只适用于共点力的合成,对非共点力的合成不适用。②今后我们所研究的问题,凡是涉及力的运算的题目,都是关于共点力方向的问题。
学点2 共点力
⑴共点力:一个物体受到两个或更多个力的作用,若它们的作用线交于一点或作用线的延长线交于一点,这一组力就是共点力。
⑵平行四边形定则只适用于共点力。
【例2】有5个力作用于一点O,这5个力构成一个正六边
形的两邻边和三条对角线,如图3-4-5所示,设F3=
10 N, 则这5 个合力的大小为多少?
【答案】30N
图3-4-5
【解析】根据图形的对称性和力的平行四边形定则求解。
解法一:根据对称性,其合力的方向一定沿力F3的方向(F1与F5合成,F2与F4合成)。在图中作出这些力合成的平行四边形,由图3-4-6可知力F1与F5的夹角为120°,它们的大小相等,合力在其夹角的平分线上,合力大小等于其分力的大小,故力F1与F5合力大小为F15=(1/2)F3=5 N。同理,力F2与F4的合力大小也在其夹角平分线上,由图中几何关系可得F24=F3+F15=15 N。所以合力F=F15+F24+F3=(5+15+10) N=30 N。
解法二:根据矢量三角形和对称性求解。
将矢量F1、F5移到对边,如图3-4-7所示,由图可知:F1、F4的合力等于 F3,F2、F5的合力等于F3,所以,5个力合成的结果为3F3=30 N。显然这种合成的方式比上一种合成方式更好,这是分析图中力的特点所采用最为简捷的方法。
图3-4-7
图3-4-6
两个大小相等的共点力F1和F2,它们之间的夹角为90°时,合力大小为20N,则当它们之间的夹角为120°时,合力大小为( )
A.40N B.10 N
C.20 N D.10 N
B
2
1.合力与分力的大小关系是怎样的?
2.三个力的合力最小值一定是零吗?
不是。设三个力大小分别为F1、F2、F3,其合力的最大值为Fmax=F1+F2+F3。
合力最小值的确定:三个共点力的数值如果能构成三角形,则合力的最小值为零;若三个力构不成三角形,则最小值为最大力减去两个较小力。能构成三角形的意思就是某一力大于另两力之差小于这两力之和。
由平行四边形可知:F1、F2夹角变化时,合力F的大小和方向也发生变化。
(1)合力F的范围:|F1-F2|≤F≤F1+F2。
①两分力同向时,合力F最大,F=F1+F2。
②两分力反向时,合力F最小,F=|F1-F2|。
③两分力有一夹角θ时,如图甲所示,在平行四边形OABC中,将F2平移到F1末端,则F1F2F围成一个闭合三角形。如图乙所示,
由三角形知识可知;
|F1-F2|<F<F1+F2。
综合以上三种情况可知
|F1-F2|≤F≤F1+F2。
(2)两分力夹角越大,合力就越小。
(3)合力可能大于某一分力,也可能小于任一分力.
退出
第三章 相互作用
学案4 力的合成
一首优美动听的《清江放排》勾勒出了一幅放排工艰辛劳动的情景,在逆水行舟时,放排工在岸上背驼缆绳,唱着响亮的劳动号子,将竹排在逆水中向前缓慢拉动,如图所示。
你能从力学的角度上解释它的道理吗?
假设有机动船的话,就不要人拉了。机
械推力就可以使船逆水而上,但在没有机械
动力的情形下,两岸的拉力F1、F2可以产生与机械动力相同的效果——也能使船逆水而上。
学点1 力的合成
⑴合力与分力
①定义:一个力产生的效果跟几个力的共同作用产生的效果相同,则这个力就叫那几个力的合力,那几个力叫做分力。
②两点诠释合力与分力的关系。
a.合力与分力是一种等效替代的关系,即分力与合力虽然不同时作用在物体上,但可以相互替代,能够相互替代的条件是分力和合力的作用效果相同,但不能同时考虑分力的作用与合力的作用。
b.两个力的作用效果可以用一个力替代,进一步想,满足一定条件的多个力的作用效果也可由一个力来替代。
⑵力的合成
①定义:求几个力的合力的过程叫做力的合成。
②说明:力的合成的实质是找一个力去替代作用在物体上的几个已知的力,而不改变其作用效果的方法。
(3)探究力的合成的法则
实验装置如图3-4-1所示。
探究过程:①在长木板上用图钉固定一张白纸,在白纸上用图
钉固定一个橡皮筋;
②在橡皮筋的另一端拴上两个细绳套,用两个弹簧测力计互成
角度地拉橡皮筋,记下结点的位置O,弹簧测力计的示数和细绳套
的方向,即两分力F1、F2的大小和方向;
③再用一个弹簧测力计拉细绳套,拉到结点位置O,记下此时
的力F的大小和方向;
④选定标度,作出力F1、F2、F的图示;
⑤以F1、F2为邻边作平行四边形,并作出对角线,如图3-4
-2所示。
实验结论:F和对角线F′在误差范围内重合,说明两个力合成
时,用表示这两个力的线段为邻边作平行四边形,则平行四边形的对
角线所代表的力与合力的大小和方向是相同的。
注意事项:①在使用弹簧测力计拉细绳套时,要使测力计的弹簧
与细绳套在同一直线上,弹簧与木板面平行,避免弹簧与测力计壳有
摩擦;
②作力的图示时,标度要统一。
图3-4-1
图3-4-2
(4)平行四边形定则
①内容:两个力合成时,以表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向,这个法则叫做平行四边形定则。
说明:平行四边形定则是矢量运算的基本法则。
②应用平行四边形定则求合力的三点注意
a.力的标度要适当
b.虚线、实线要分清,表示分力和合力的两条邻边和对角线画实线,并加上箭头,平行四边形的另两条边画虚线;
c.求合力时既要求出合力的大小,还要求出合力的方向,不要忘了用量角器量出合力与某一分力间的夹角。
【例1】两个小孩拉一辆车子,一个小孩用的力是45 N,另一个小孩用的力是60 N,
这两个力的夹角是90°,求它们的合力。
【答案】合力大小为75 N,方向与45 N的力成53°角。
【解析】解法一:如图3-4-3甲所示,选择标度,作出F1、F2的图示,利用三角板作出平行四边形,画出对角线,用15 N的标度去度量F,得出F=75 N。再用量角器
量得F与F1之间的夹角为53°。
解法二:根据平行四边形定
则,作出如图3-4-3乙所示的力
的示意图,利用勾股定理求出合力。
N=75 N,
tanθ=F2/F1=60/45≈1.33,
所以θ=53°。
甲 乙
图3-4-3
【评析】求两分力的合力的方法一般有两种:①图解法;②计算法,利用这两种方法各有利弊,图解法简单、直观,但不精确;计算法虽然精确,但对学生数学水平要求较高。
1
如图3-4-4所示,为使电线杆稳定,在杆上加了两根拉线CA和CB,若每根拉线的拉力都是330 N,两根拉线间的夹角为60°角.求拉线拉力的合力大小和方向.
【答案】520 N 向竖直向下
图3-4-4
⑶多个力合成的方法
如果有两个以上共点力作用在物体上,我们也可以应用平行四边形定则求出它们的合力:先求出任意两个力的合力,再求出这个合力跟第三个力的合力,直到把所有的力都合成进去,最后得到的结果就是这些力的合力。
说明:①平行四边形定则只适用于共点力的合成,对非共点力的合成不适用。②今后我们所研究的问题,凡是涉及力的运算的题目,都是关于共点力方向的问题。
学点2 共点力
⑴共点力:一个物体受到两个或更多个力的作用,若它们的作用线交于一点或作用线的延长线交于一点,这一组力就是共点力。
⑵平行四边形定则只适用于共点力。
【例2】有5个力作用于一点O,这5个力构成一个正六边
形的两邻边和三条对角线,如图3-4-5所示,设F3=
10 N, 则这5 个合力的大小为多少?
【答案】30N
图3-4-5
【解析】根据图形的对称性和力的平行四边形定则求解。
解法一:根据对称性,其合力的方向一定沿力F3的方向(F1与F5合成,F2与F4合成)。在图中作出这些力合成的平行四边形,由图3-4-6可知力F1与F5的夹角为120°,它们的大小相等,合力在其夹角的平分线上,合力大小等于其分力的大小,故力F1与F5合力大小为F15=(1/2)F3=5 N。同理,力F2与F4的合力大小也在其夹角平分线上,由图中几何关系可得F24=F3+F15=15 N。所以合力F=F15+F24+F3=(5+15+10) N=30 N。
解法二:根据矢量三角形和对称性求解。
将矢量F1、F5移到对边,如图3-4-7所示,由图可知:F1、F4的合力等于 F3,F2、F5的合力等于F3,所以,5个力合成的结果为3F3=30 N。显然这种合成的方式比上一种合成方式更好,这是分析图中力的特点所采用最为简捷的方法。
图3-4-7
图3-4-6
两个大小相等的共点力F1和F2,它们之间的夹角为90°时,合力大小为20N,则当它们之间的夹角为120°时,合力大小为( )
A.40N B.10 N
C.20 N D.10 N
B
2
1.合力与分力的大小关系是怎样的?
2.三个力的合力最小值一定是零吗?
不是。设三个力大小分别为F1、F2、F3,其合力的最大值为Fmax=F1+F2+F3。
合力最小值的确定:三个共点力的数值如果能构成三角形,则合力的最小值为零;若三个力构不成三角形,则最小值为最大力减去两个较小力。能构成三角形的意思就是某一力大于另两力之差小于这两力之和。
由平行四边形可知:F1、F2夹角变化时,合力F的大小和方向也发生变化。
(1)合力F的范围:|F1-F2|≤F≤F1+F2。
①两分力同向时,合力F最大,F=F1+F2。
②两分力反向时,合力F最小,F=|F1-F2|。
③两分力有一夹角θ时,如图甲所示,在平行四边形OABC中,将F2平移到F1末端,则F1F2F围成一个闭合三角形。如图乙所示,
由三角形知识可知;
|F1-F2|<F<F1+F2。
综合以上三种情况可知
|F1-F2|≤F≤F1+F2。
(2)两分力夹角越大,合力就越小。
(3)合力可能大于某一分力,也可能小于任一分力.
退出
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
