2011-2012学年高一物理必修1(人教版)学案课件第三章 相互作用3.5 力的分解
文档属性
| 名称 | 2011-2012学年高一物理必修1(人教版)学案课件第三章 相互作用3.5 力的分解 |

|
|
| 格式 | rar | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2011-09-12 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
第三章 相互作用
学案5 力的分解
多个力同时作用在一个物体上,可以产生一个效果。反之,作用在物体上的一个力也可以产生几个效果。
沿着某方向作用的一个力,确定能产生其他方向的作用效果。这些效果就是由这个力的分力产生的。所以在实际应用中,常常需要对力进行分解。
学点1 力的分解
(1)定义:作用在物体上的一个力的作用效果,与几个力的作用效果相同,则这几个力叫做该力的分力。已知合力求分力叫做力的分解。
(2)力的分解是力的合成的逆运算。
(3)力的分解遵循平行四边形定则:把一个已知力作为平行四边形的对角线,则与已知力共点的平行四边形的两个邻边就表示已知力的两个分力。
(4)如果没有其他限制,对于一条对角线,可以作出无数个不同的平行四边形,如图3-5-1所示。即同一个力F可以分解成无数对大
小、方向不同的分力。
(5)力的分解的方法和步骤
①首先是要根据这个力的实际作用效果确定两个实际
分力的方向。
②再根据两个实际分力方向作平行四边形,已知力为
对角线,实际分力为邻边。
③然后根据平行四边形知识和相关的数学知识,求出
两分力的大小和方向。
图3-5-1
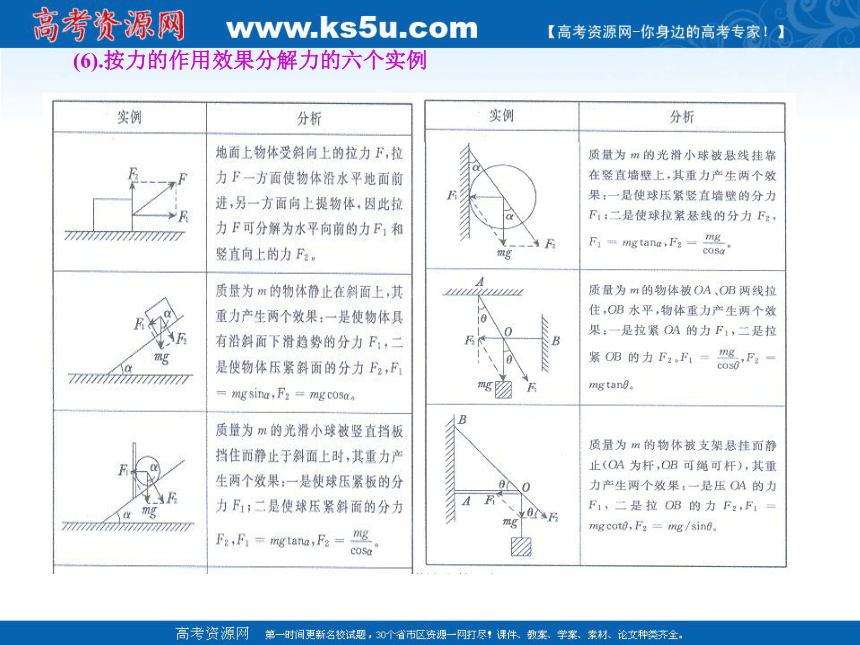
(6).按力的作用效果分解力的六个实例
【例1】沿光滑的墙壁用网兜把一个足球挂在A点,如图3-5-2所示,
足球的质量为m,网兜的质量不计,足球与墙壁的接触点为B,
悬绳与墙壁的夹角为α。求足球对绳的拉力和对墙壁的压力的
大小。
【答案】mg/cosα mgtanα
【答案】 N N
1
在倾角α=30°的斜面上有一块竖直放置的挡板,在挡板和斜面之间放有一个重为G=20 N的光滑圆球,如图3-5-4所示,试求这个球对斜面的压力和对挡板的压力。
图3-5-4
【解析】物体的重力产生两个效果:拉紧绳子和挤压墙壁。所以
将重力沿着这两个方向进行分解,其受力如图3-5-3所示。
通过解三角形可以求得F2=Gtanα=mgtanα。
F1=G/cosα=mg/cosα。
足球对绳的拉力大小等于绳对足球的拉力,即F1′=F1=mg/cosα,足球对墙壁的压力大小等于F2′=F2=mgtanα。
图3-5-3
图3-5-2
学点2 矢量相加的法则
(2)矢量与标量
①矢量:既有大小又有方向,相加时遵从平行四边形定则(或三角形定则)的物理量。如速度、位移、加速度等。
②标量:只有大小,没有方向,求和时按照算术法则相加的物理量。如质量、时间等。
注意:矢量和标量的本质区别在于它们的运算法则不同。矢量按照平行四边形法则运算,标量按照算术法则运算。
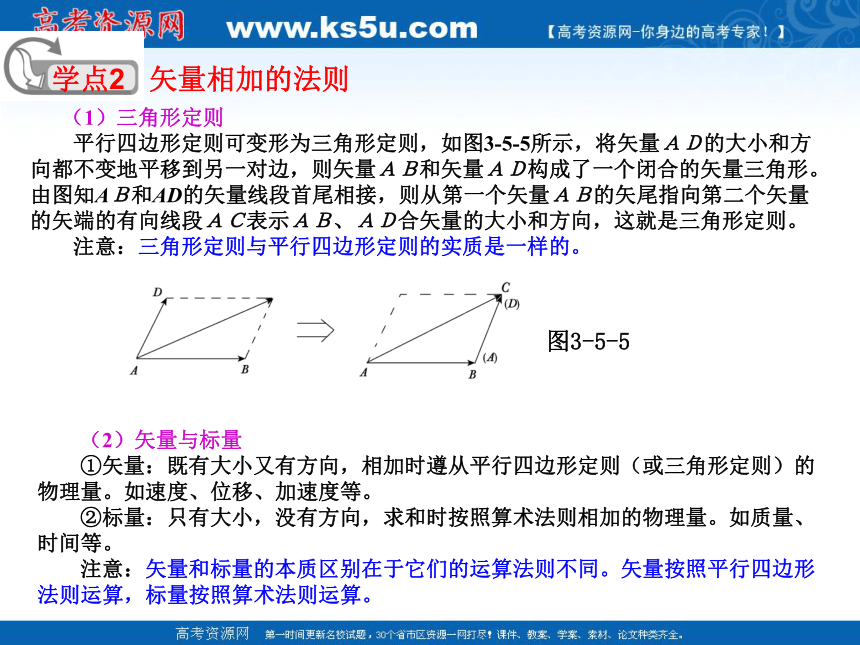
(1)三角形定则
平行四边形定则可变形为三角形定则,如图3-5-5所示,将矢量AD的大小和方向都不变地平移到另一对边,则矢量AB和矢量AD构成了一个闭合的矢量三角形。由图知AB和AD的矢量线段首尾相接,则从第一个矢量AB的矢尾指向第二个矢量的矢端的有向线段AC表示AB、AD合矢量的大小和方向,这就是三角形定则。
注意:三角形定则与平行四边形定则的实质是一样的。
图3-5-5
AC
图3-5-6
一架质量为4 000 kg的歼击机,在5.0×105 N推力作用下由静止开始起飞,飞行方向与水平方向成30°角,飞行加速度为10 m/s2,如图3-5-7所示,求:
⑴起飞20 s后,飞机距离地面的高度;
⑵起飞20 s后,飞机在水平方向的分速度vx
和竖直方向的分速度vy;
⑶飞机起飞过程中受到竖直向上的推力Fy和
竖直向上的加速度各是多大?
2
【答案】⑴1 000 m ⑵ vy=100 m/s
⑶Fy=2.5×105 N a=5.0 m/s2
图3-5-7
力的分解有解或无解,简单地说是代表合力的对角线与给定的代表分力的有向线段是否构成平行四边形(或三角形)。若可以构成平行四边形(或三角形),说明合力可以分解成给定分力,即有解;若不能,则无解。常见的四种分解情况有
1.常见的力的分解有哪几种情况,分别是怎样的?
已知条件 示意图 解的情况
已知合力和两个分力的方向 有唯一解
已知合力和两个分力的大小 有两解或无解(当|F1-F2|已知合力和一个分力的大小和方向 有唯一解(可由三角形确定)
已知合力和一个分力的大小和另一个分力的方向 (1)F2=F·sinθ或F2>F时,有一解,且F·sinθ是F2的最小值。(2)当F2<F·sinθ时无解。(3)当F·sinθ<F2<F时,有两解。
2.如何利用正交分解法求合力?
(1)正交分解的方法
同一直线上的两个或多个力,其合力可由代数运算求得,当物体受到多个不共线的力时,其合力用平行四边形定则求解很不方便,此时我们可以考虑利用正交分解法,即把各力正交分解在互相垂直的坐标轴上,分别求出两个不同方向上的合力Fx和Fy。然后再由F= 求合力,由tanθ=Fy/Fx确定合力的方向。
(2)正解分解法的步骤
①建立直角坐标系,建立坐标系时,要让尽可能多的力落到坐标轴上,即需要分解的力尽可能地少。
②各力分别沿x轴、y轴分解。
③分别求出x轴上的合力Fx和y轴上的合力Fy。
④则合力的大小F= ,设合力与x轴夹角为θ,则tanθ=Fy/Fx。
退出
第三章 相互作用
学案5 力的分解
多个力同时作用在一个物体上,可以产生一个效果。反之,作用在物体上的一个力也可以产生几个效果。
沿着某方向作用的一个力,确定能产生其他方向的作用效果。这些效果就是由这个力的分力产生的。所以在实际应用中,常常需要对力进行分解。
学点1 力的分解
(1)定义:作用在物体上的一个力的作用效果,与几个力的作用效果相同,则这几个力叫做该力的分力。已知合力求分力叫做力的分解。
(2)力的分解是力的合成的逆运算。
(3)力的分解遵循平行四边形定则:把一个已知力作为平行四边形的对角线,则与已知力共点的平行四边形的两个邻边就表示已知力的两个分力。
(4)如果没有其他限制,对于一条对角线,可以作出无数个不同的平行四边形,如图3-5-1所示。即同一个力F可以分解成无数对大
小、方向不同的分力。
(5)力的分解的方法和步骤
①首先是要根据这个力的实际作用效果确定两个实际
分力的方向。
②再根据两个实际分力方向作平行四边形,已知力为
对角线,实际分力为邻边。
③然后根据平行四边形知识和相关的数学知识,求出
两分力的大小和方向。
图3-5-1
(6).按力的作用效果分解力的六个实例
【例1】沿光滑的墙壁用网兜把一个足球挂在A点,如图3-5-2所示,
足球的质量为m,网兜的质量不计,足球与墙壁的接触点为B,
悬绳与墙壁的夹角为α。求足球对绳的拉力和对墙壁的压力的
大小。
【答案】mg/cosα mgtanα
【答案】 N N
1
在倾角α=30°的斜面上有一块竖直放置的挡板,在挡板和斜面之间放有一个重为G=20 N的光滑圆球,如图3-5-4所示,试求这个球对斜面的压力和对挡板的压力。
图3-5-4
【解析】物体的重力产生两个效果:拉紧绳子和挤压墙壁。所以
将重力沿着这两个方向进行分解,其受力如图3-5-3所示。
通过解三角形可以求得F2=Gtanα=mgtanα。
F1=G/cosα=mg/cosα。
足球对绳的拉力大小等于绳对足球的拉力,即F1′=F1=mg/cosα,足球对墙壁的压力大小等于F2′=F2=mgtanα。
图3-5-3
图3-5-2
学点2 矢量相加的法则
(2)矢量与标量
①矢量:既有大小又有方向,相加时遵从平行四边形定则(或三角形定则)的物理量。如速度、位移、加速度等。
②标量:只有大小,没有方向,求和时按照算术法则相加的物理量。如质量、时间等。
注意:矢量和标量的本质区别在于它们的运算法则不同。矢量按照平行四边形法则运算,标量按照算术法则运算。
(1)三角形定则
平行四边形定则可变形为三角形定则,如图3-5-5所示,将矢量AD的大小和方向都不变地平移到另一对边,则矢量AB和矢量AD构成了一个闭合的矢量三角形。由图知AB和AD的矢量线段首尾相接,则从第一个矢量AB的矢尾指向第二个矢量的矢端的有向线段AC表示AB、AD合矢量的大小和方向,这就是三角形定则。
注意:三角形定则与平行四边形定则的实质是一样的。
图3-5-5
AC
图3-5-6
一架质量为4 000 kg的歼击机,在5.0×105 N推力作用下由静止开始起飞,飞行方向与水平方向成30°角,飞行加速度为10 m/s2,如图3-5-7所示,求:
⑴起飞20 s后,飞机距离地面的高度;
⑵起飞20 s后,飞机在水平方向的分速度vx
和竖直方向的分速度vy;
⑶飞机起飞过程中受到竖直向上的推力Fy和
竖直向上的加速度各是多大?
2
【答案】⑴1 000 m ⑵ vy=100 m/s
⑶Fy=2.5×105 N a=5.0 m/s2
图3-5-7
力的分解有解或无解,简单地说是代表合力的对角线与给定的代表分力的有向线段是否构成平行四边形(或三角形)。若可以构成平行四边形(或三角形),说明合力可以分解成给定分力,即有解;若不能,则无解。常见的四种分解情况有
1.常见的力的分解有哪几种情况,分别是怎样的?
已知条件 示意图 解的情况
已知合力和两个分力的方向 有唯一解
已知合力和两个分力的大小 有两解或无解(当|F1-F2|
已知合力和一个分力的大小和另一个分力的方向 (1)F2=F·sinθ或F2>F时,有一解,且F·sinθ是F2的最小值。(2)当F2<F·sinθ时无解。(3)当F·sinθ<F2<F时,有两解。
2.如何利用正交分解法求合力?
(1)正交分解的方法
同一直线上的两个或多个力,其合力可由代数运算求得,当物体受到多个不共线的力时,其合力用平行四边形定则求解很不方便,此时我们可以考虑利用正交分解法,即把各力正交分解在互相垂直的坐标轴上,分别求出两个不同方向上的合力Fx和Fy。然后再由F= 求合力,由tanθ=Fy/Fx确定合力的方向。
(2)正解分解法的步骤
①建立直角坐标系,建立坐标系时,要让尽可能多的力落到坐标轴上,即需要分解的力尽可能地少。
②各力分别沿x轴、y轴分解。
③分别求出x轴上的合力Fx和y轴上的合力Fy。
④则合力的大小F= ,设合力与x轴夹角为θ,则tanθ=Fy/Fx。
退出
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
