人教版小学数学五年级上册讲义 多边形的认识
文档属性
| 名称 | 人教版小学数学五年级上册讲义 多边形的认识 |
|
|
| 格式 | docx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 00:00:00 | ||
图片预览

文档简介
多边形的认识
学生姓名
年级
学科
授课教师
日期
时段
核心内容
多边形的特征、面积、周长的求法
课型
一对一/一对N
教学目标
1、使学生掌握规则图形的特征、面积、周长的求法
2、使学生会求组合图形的面积、不规则图形的面积和周长
3、使学生掌握求阴影部分的面积
重、难点
求组合图形的面积、求阴影部分的面积
2532380114300
课首沟通
我们以前学的基本的平面图形有哪些?他们的面积和周长分别是什么? 基本图形面积求导公式之间的有什么关系?
368300273685知识导图
课首小测
一个平行四边形的底为15分米,高为18分米,面积为( )平方分米。如果一个平行四边形底为12分米,面积为
180平方分米,则高为( )分米。
一个平行四边形的底扩大4倍,高缩小2倍,则面积( );如果它的底缩小3倍,高扩大3倍,则面积( )。
一个梯形的面积是42平方米,它的上下底之和与一个平行四边形的底边相等,高与平行四边形的高相等,这个平行四 边形的面积是( )平方米。
一块直角三角形的地,两条直角边的长分别是36米、27米,这块地的面积是( )平方米。
一个长方形木框,长10dm,宽8dm,将它拉成一个平行四边形,面积变( ),这个平行四边形的周长为( )dm。
368300290830知识梳理
导学一 : 长方形和正方形的面积和周长
知识点讲解
例 1. 用四个相同的长方形拼成一个面积为100平方厘米的的大正方形,每个长方形的周长是多少厘米?
6149340240665
例 2. 有一块长方形草地,长20米,宽15米。在它的四周向外筑一条宽2米的小路,求小路的面积?
5825490241300
我爱展示
一个周长72厘米的长方形,它是由三个大小相等的正方形拼成的,求一个正方形的面积是多少?
有一个正方形草坪,沿草坪四周向外修建1米宽的小路,小路路面面积是80平方米。求草坪的面积是多少平方米?
6084570240665
导学二 : 平行四边形、三角形面积
知识点讲解 1:三角形的面积
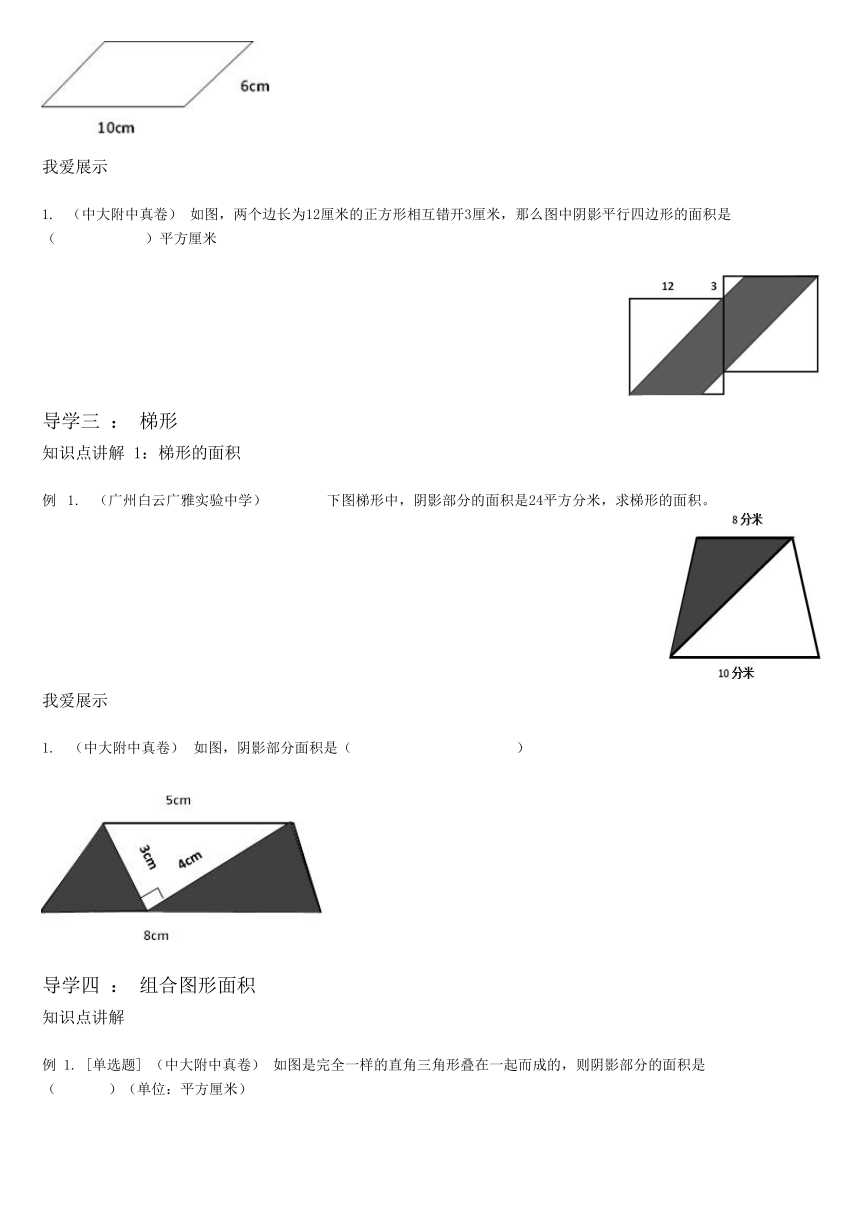
460375190500例 1. (实验中学天河校区数学真卷) 图中是有两个边长分别为a、b的两个正方形拼成的。
①用含字母的式子表示图中阴影部分的面积是( )。
②当a=5,b=4时,图中阴影部分的面积是( )。
368300403225例 2. [单选题] (中大附中数学真卷) 将一张长5厘米,宽3厘米的长方形纸沿对角线对折后如图所示,图中阴影部分的周长是( )
A. 8 B. 13 C. 16
我爱展示
368300227330[单选题] 梯形ABCD中,三角形AOD和三角形BOC的面积相比( )
三角形AOD B.三角形BOC C.一样大 D.无法比较
知识点讲解 2:平行四边形的面积
例 1. (中大附中真卷) 如图是一个平行四边形,其中一条底上的高是6cm,则这个平行四边形的面积是
( )平方厘米
我爱展示
(中大附中真卷) 如图,两个边长为12厘米的正方形相互错开3厘米,那么图中阴影平行四边形的面积是
( )平方厘米
5529580248285
导学三 : 梯形
知识点讲解 1:梯形的面积
5890260198755例 1. (广州白云广雅实验中学) 下图梯形中,阴影部分的面积是24平方分米,求梯形的面积。
我爱展示
1. (中大附中真卷) 如图,阴影部分面积是( )
368300170815
导学四 : 组合图形面积
知识点讲解
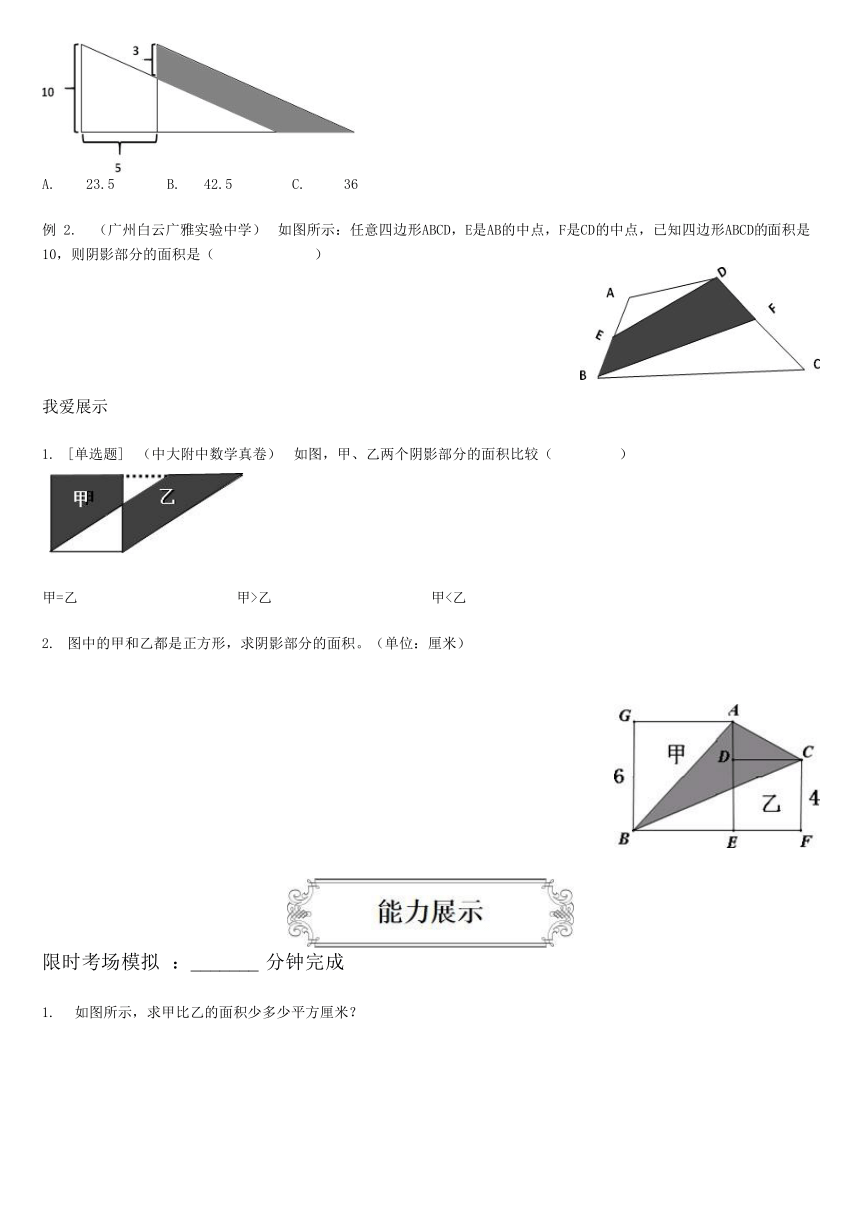
例 1. [单选题] (中大附中真卷) 如图是完全一样的直角三角形叠在一起而成的,则阴影部分的面积是
( )(单位:平方厘米)
A. 23.5 B. 42.5 C. 36
5111750412115例 2. (广州白云广雅实验中学) 如图所示:任意四边形ABCD,E是AB的中点,F是CD的中点,已知四边形ABCD的面积是10,则阴影部分的面积是( )
我爱展示
[单选题] (中大附中数学真卷) 如图,甲、乙两个阴影部分的面积比较( )
43243592710
甲=乙 甲>乙 甲<乙
图中的甲和乙都是正方形,求阴影部分的面积。(单位:厘米)
540956512763525323801663065
限时考场模拟 : 分钟完成
如图所示,求甲比乙的面积少多少平方厘米?
5472430245110求下图阴影部分的面积。(单位:厘米)
下图是两个相同的直角梯形重叠在一起,求阴影部分的面积.(单位:厘米)
368300240030
课后作业
边长为4厘米的正方形,它的周长和面积相等。 ( )
任意两个三角形都可以拼成一个梯形。( )
一个三角形底长10cm,如果底延长1cm,面积就增加2cm2,原来三角形的面积是多少平方厘米?
375920548640(广州小联盟考试) 如图,ABCD是一个长方形,AB=10cm,AD=4cm,E、F分别是BC、AD的中点,G是线段CD上的任意一点,则图中国阴影部分的面积为( )cm2
已知正方形甲的边长是6厘米,正方形乙的面积是81平方厘米,那么图中阴影部分的面积是多少?
如图,平行四边形BCEF中,BC=8厘米,直角三角形中,AC=10厘米,阴影部分面积比三角形ADH的面积大8平方厘米。 求AH长多少厘米?
609219013398525323801365885
1、学完这节课的内容后,完成本堂课的课后作业。
2、标注理解不够深刻的例题回去复习。本堂课中的错题要写到错题本上,下节课会对错题进行练习。
3、深入理解基本平面图形与组合图形之间的关系,灵活运用已学过的知识去解决不规则图形的面积和周长问题。
4、总结求多边形面积的题型特征。
2532380212090
课首小测
1.270;15
2.扩大两倍;不变
3.84
4.486
5.小;36
导学一
知识点讲解例题
1.20cm
解析:每个长方形的长加宽的和等于正方形的边长,根据正方形的面积是100平方厘米,求出正方形的边长,也就是长方 形长加宽的和,再乘2就得长方形的周长。
解答过程:10×10=100(cm2), 10×2=20(cm) 2.156平方米
解析:求小路的面积,因为小路是不规则图形,所以转化成先求草坪的面积20×15=300(平方米),再求外面大长方形的 面积(20+4)×(15+4)=456(平方米),易错点不是长加2,而是加4,最后用外面大长方形的面积减去里面草坪的面 积就是小路的面积。
解答过程:20×15=300(平方米),(20+4)×(15+4)=456(平方米),456-300=156(平方米)
我爱展示
1.81cm2
6417945480060解析:如图所示,三个正方形拼成一个长方形,只有这一种拼法,重合了四条边,故少了四条边,3×4-4=8总共还有8条 边,长度为72厘米,求出了正方形的边长:72÷8=9(cm),则正方形的面积为9×9=81(cm2)
2.361 m2
解析:四个顶点处的小正方形的面积都是1×1=1(m2)
小路路面面积减去四个小正方形的面积就是剩下四个完全一样的长方形的面积80-1×4=76(m2),那么一个小长方形的 面积就是76÷4=19(m2),又因为小长方形的宽是1米,故小长方形的宽是19÷1=19(m),即草坪的边长是19米,则草坪 的面积是:19×19=361(m2)
6075680215900解答过程: 1×1=1(m2),(80-1×4)÷4=19(m2), 19÷1=19(m), 19×19=361(m2)
导学二
知识点讲解 1:三角形的面积例题
1.a(a+b)÷2;22.5
解析:用字母表示数的时候三角形对应的底是a,三角形对应的高是(a+b),利用三角形的面积公式得到三角形的面积a(a+b)÷2;然后当a=5,b=4时,直接将数值代入第一问求出的式子,算出的数即可5×(5+4)÷2=22.5
2.C
解析:BC=ED=5cm,BE=CD=3cm
故阴影部分的周长是(5+3)×2=16(cm)
5853430110490
我爱展示
1.C
解析:三角形ACD与三角形BCD底相同,高也有共同的高,因此三角形ACD与三角形BCD面积相同,这两个三角形减去同一个 三角形DOC,分别得到三角形AOD和三角形BOC,因此三角形AOD与三角形BOC的面积相等
知识点讲解 2:平行四边形的面积例题
1.36
解析:因为直角三角形中斜边最长故只能是边长为6cm的边
作为底边,该边上的高是6cm,故平行四边形的面积是6×6=36(cm2)
我爱展示
1.135
解析:根据题意求出图中阴影平行四边形的底和高,再根据平行四边形的面积公式计算即可底:12-3=9(cm),高(12+3)=15(cm)则面积为9×15=135(cm2)
导学三
知识点讲解 1:梯形的面积例题
1.54dm2
解析:先以8分米的边为底,求三角形的高,即求梯形的高24×2÷8=6(dm),然后利用梯形的面积公式来求解梯形的面 积(10+8)×6÷2=54(dm2)
我爱展示
1.9.6cm2
解析:先利用三角形的面积公式求出三角形斜边上的高,直角三角形的面积3×4÷2=6(cm2),等积变换求出三角形斜边 上的高6×2÷5=2.4(cm)。因为三角形的高和梯形的高是一样的,然后再利用梯形的面积公式求出整个梯形的面积,最 后利用梯形的面积减去三角形的面积就是阴影部分的面积即:
(5+8)×2.4÷2-6=9.6(cm2)
导学四
知识点讲解例题
1.B
解析:因为原来是由两个完全一样的三角形重叠在一起而形成的图形,故两个三角形的面积是相等的,那么两个三角形同 时减去重叠部分的面积,剩下部分的面积相等。一个三角形剩下的部分是梯形,一个三角形剩下的部分是阴影部分,求 阴影部分的面积就相当于求梯形的面积则有(10-3+10)×5÷2=42.5(cm2)
2.5
解析:连接BD,则三角形EAD与三角形EBD面积相等;三角形FDB与三角形FCB面积相等,则阴影部分的面积是整个四边形面 积的一半,即:10÷2=5
我爱展示
1.A
解析:长方形和平行四边形是等底等高的,因此长方形和正方形的面积相等,图中空白部分是长方形和平行四边形重合的 部分,面积也相等,长方形和平行四边形同时减去空白部分,所剩下的阴影部分的面积也相等。
2.18cm2
解析:6×(6+4)=60(cm2),60-6×6÷2-(4+6)×4÷2-(6-4)×4÷2=18(cm2)
将整个图形补成一个大长方形,然后用大长方形的面积减去三个三角形的面积,所得结果即为阴影部分的面积
限时考场模拟
1.3cm2
解析:(5+4)×6÷2=27(cm2), 4×6=24(cm2),27-24=3(cm2)
求甲乙面积的差,与大三角形的面积减去长方形的面积相等。因为大三角形的面积=甲的面积+空白部分的面积 ,长方形
的面积=乙的面积+空白部分的面积,二者相减,则空白部分相抵消,就是甲乙面积差。2.135cm2
解析:15×18÷2=135(cm2) 3.36cm2
解析:(10-2+10)×4÷2=36(cm2)
因为最初两个梯形的面积相等,它们重合的部分也相等,即空白部分,所以阴影部分的面积就和下面小直角梯形的面积 相等。
课后作业
1.错
解析:面积和周长的单位不同,所表示的意义也不同,即使求出来的数值相等,两者也是不可以比较的。2.错
解析:并不是任意两个三角形都可以拼成梯形的3.20平方厘米
解析:2×2÷1=4(cm),10×4÷2=20(cm2) 4.10
解析:三角形AFG的面积为AF×DG÷2,三角形CEG的面积CE×CG÷2 阴影部分的面积:AF×DG÷2+CE×CG÷2
=AF×(DG+GC)÷2
=AF×DC÷2
=2×10÷2
=10 (cm2)
5.19平方厘米
解析:用整个图形的面积:两个正方形的面积和减去空白部分三个三角形的面积,即为阴影部分的面积。解答过程:81÷9=9(cm),(9+6)×9÷2+9×(9-6)÷2+6×6÷2=99(cm2),6×6+81-99=18(cm2) 6.4厘米
解析:阴影部分的面积与三角形ADH的面积差与平行四边形BCEF和三角形ABC的面积差相等。解:设AH长为Xcm。
8×(10-X)-8×10÷2=8
80-8X-40=8
40-8X=8
8X=32 X=4
或三角形ABC的面积:8×10÷2=40(cm2)
平行四边形比三角形的面积多8 cm2则平行四边形的面积40+8=48(cm2) 则CH的长度为48÷8=6(cm),故AH的长度为10-6=4(cm)
学生姓名
年级
学科
授课教师
日期
时段
核心内容
多边形的特征、面积、周长的求法
课型
一对一/一对N
教学目标
1、使学生掌握规则图形的特征、面积、周长的求法
2、使学生会求组合图形的面积、不规则图形的面积和周长
3、使学生掌握求阴影部分的面积
重、难点
求组合图形的面积、求阴影部分的面积
2532380114300
课首沟通
我们以前学的基本的平面图形有哪些?他们的面积和周长分别是什么? 基本图形面积求导公式之间的有什么关系?
368300273685知识导图
课首小测
一个平行四边形的底为15分米,高为18分米,面积为( )平方分米。如果一个平行四边形底为12分米,面积为
180平方分米,则高为( )分米。
一个平行四边形的底扩大4倍,高缩小2倍,则面积( );如果它的底缩小3倍,高扩大3倍,则面积( )。
一个梯形的面积是42平方米,它的上下底之和与一个平行四边形的底边相等,高与平行四边形的高相等,这个平行四 边形的面积是( )平方米。
一块直角三角形的地,两条直角边的长分别是36米、27米,这块地的面积是( )平方米。
一个长方形木框,长10dm,宽8dm,将它拉成一个平行四边形,面积变( ),这个平行四边形的周长为( )dm。
368300290830知识梳理
导学一 : 长方形和正方形的面积和周长
知识点讲解
例 1. 用四个相同的长方形拼成一个面积为100平方厘米的的大正方形,每个长方形的周长是多少厘米?
6149340240665
例 2. 有一块长方形草地,长20米,宽15米。在它的四周向外筑一条宽2米的小路,求小路的面积?
5825490241300
我爱展示
一个周长72厘米的长方形,它是由三个大小相等的正方形拼成的,求一个正方形的面积是多少?
有一个正方形草坪,沿草坪四周向外修建1米宽的小路,小路路面面积是80平方米。求草坪的面积是多少平方米?
6084570240665
导学二 : 平行四边形、三角形面积
知识点讲解 1:三角形的面积
460375190500例 1. (实验中学天河校区数学真卷) 图中是有两个边长分别为a、b的两个正方形拼成的。
①用含字母的式子表示图中阴影部分的面积是( )。
②当a=5,b=4时,图中阴影部分的面积是( )。
368300403225例 2. [单选题] (中大附中数学真卷) 将一张长5厘米,宽3厘米的长方形纸沿对角线对折后如图所示,图中阴影部分的周长是( )
A. 8 B. 13 C. 16
我爱展示
368300227330[单选题] 梯形ABCD中,三角形AOD和三角形BOC的面积相比( )
三角形AOD B.三角形BOC C.一样大 D.无法比较
知识点讲解 2:平行四边形的面积
例 1. (中大附中真卷) 如图是一个平行四边形,其中一条底上的高是6cm,则这个平行四边形的面积是
( )平方厘米
我爱展示
(中大附中真卷) 如图,两个边长为12厘米的正方形相互错开3厘米,那么图中阴影平行四边形的面积是
( )平方厘米
5529580248285
导学三 : 梯形
知识点讲解 1:梯形的面积
5890260198755例 1. (广州白云广雅实验中学) 下图梯形中,阴影部分的面积是24平方分米,求梯形的面积。
我爱展示
1. (中大附中真卷) 如图,阴影部分面积是( )
368300170815
导学四 : 组合图形面积
知识点讲解
例 1. [单选题] (中大附中真卷) 如图是完全一样的直角三角形叠在一起而成的,则阴影部分的面积是
( )(单位:平方厘米)
A. 23.5 B. 42.5 C. 36
5111750412115例 2. (广州白云广雅实验中学) 如图所示:任意四边形ABCD,E是AB的中点,F是CD的中点,已知四边形ABCD的面积是10,则阴影部分的面积是( )
我爱展示
[单选题] (中大附中数学真卷) 如图,甲、乙两个阴影部分的面积比较( )
43243592710
甲=乙 甲>乙 甲<乙
图中的甲和乙都是正方形,求阴影部分的面积。(单位:厘米)
540956512763525323801663065
限时考场模拟 : 分钟完成
如图所示,求甲比乙的面积少多少平方厘米?
5472430245110求下图阴影部分的面积。(单位:厘米)
下图是两个相同的直角梯形重叠在一起,求阴影部分的面积.(单位:厘米)
368300240030
课后作业
边长为4厘米的正方形,它的周长和面积相等。 ( )
任意两个三角形都可以拼成一个梯形。( )
一个三角形底长10cm,如果底延长1cm,面积就增加2cm2,原来三角形的面积是多少平方厘米?
375920548640(广州小联盟考试) 如图,ABCD是一个长方形,AB=10cm,AD=4cm,E、F分别是BC、AD的中点,G是线段CD上的任意一点,则图中国阴影部分的面积为( )cm2
已知正方形甲的边长是6厘米,正方形乙的面积是81平方厘米,那么图中阴影部分的面积是多少?
如图,平行四边形BCEF中,BC=8厘米,直角三角形中,AC=10厘米,阴影部分面积比三角形ADH的面积大8平方厘米。 求AH长多少厘米?
609219013398525323801365885
1、学完这节课的内容后,完成本堂课的课后作业。
2、标注理解不够深刻的例题回去复习。本堂课中的错题要写到错题本上,下节课会对错题进行练习。
3、深入理解基本平面图形与组合图形之间的关系,灵活运用已学过的知识去解决不规则图形的面积和周长问题。
4、总结求多边形面积的题型特征。
2532380212090
课首小测
1.270;15
2.扩大两倍;不变
3.84
4.486
5.小;36
导学一
知识点讲解例题
1.20cm
解析:每个长方形的长加宽的和等于正方形的边长,根据正方形的面积是100平方厘米,求出正方形的边长,也就是长方 形长加宽的和,再乘2就得长方形的周长。
解答过程:10×10=100(cm2), 10×2=20(cm) 2.156平方米
解析:求小路的面积,因为小路是不规则图形,所以转化成先求草坪的面积20×15=300(平方米),再求外面大长方形的 面积(20+4)×(15+4)=456(平方米),易错点不是长加2,而是加4,最后用外面大长方形的面积减去里面草坪的面 积就是小路的面积。
解答过程:20×15=300(平方米),(20+4)×(15+4)=456(平方米),456-300=156(平方米)
我爱展示
1.81cm2
6417945480060解析:如图所示,三个正方形拼成一个长方形,只有这一种拼法,重合了四条边,故少了四条边,3×4-4=8总共还有8条 边,长度为72厘米,求出了正方形的边长:72÷8=9(cm),则正方形的面积为9×9=81(cm2)
2.361 m2
解析:四个顶点处的小正方形的面积都是1×1=1(m2)
小路路面面积减去四个小正方形的面积就是剩下四个完全一样的长方形的面积80-1×4=76(m2),那么一个小长方形的 面积就是76÷4=19(m2),又因为小长方形的宽是1米,故小长方形的宽是19÷1=19(m),即草坪的边长是19米,则草坪 的面积是:19×19=361(m2)
6075680215900解答过程: 1×1=1(m2),(80-1×4)÷4=19(m2), 19÷1=19(m), 19×19=361(m2)
导学二
知识点讲解 1:三角形的面积例题
1.a(a+b)÷2;22.5
解析:用字母表示数的时候三角形对应的底是a,三角形对应的高是(a+b),利用三角形的面积公式得到三角形的面积a(a+b)÷2;然后当a=5,b=4时,直接将数值代入第一问求出的式子,算出的数即可5×(5+4)÷2=22.5
2.C
解析:BC=ED=5cm,BE=CD=3cm
故阴影部分的周长是(5+3)×2=16(cm)
5853430110490
我爱展示
1.C
解析:三角形ACD与三角形BCD底相同,高也有共同的高,因此三角形ACD与三角形BCD面积相同,这两个三角形减去同一个 三角形DOC,分别得到三角形AOD和三角形BOC,因此三角形AOD与三角形BOC的面积相等
知识点讲解 2:平行四边形的面积例题
1.36
解析:因为直角三角形中斜边最长故只能是边长为6cm的边
作为底边,该边上的高是6cm,故平行四边形的面积是6×6=36(cm2)
我爱展示
1.135
解析:根据题意求出图中阴影平行四边形的底和高,再根据平行四边形的面积公式计算即可底:12-3=9(cm),高(12+3)=15(cm)则面积为9×15=135(cm2)
导学三
知识点讲解 1:梯形的面积例题
1.54dm2
解析:先以8分米的边为底,求三角形的高,即求梯形的高24×2÷8=6(dm),然后利用梯形的面积公式来求解梯形的面 积(10+8)×6÷2=54(dm2)
我爱展示
1.9.6cm2
解析:先利用三角形的面积公式求出三角形斜边上的高,直角三角形的面积3×4÷2=6(cm2),等积变换求出三角形斜边 上的高6×2÷5=2.4(cm)。因为三角形的高和梯形的高是一样的,然后再利用梯形的面积公式求出整个梯形的面积,最 后利用梯形的面积减去三角形的面积就是阴影部分的面积即:
(5+8)×2.4÷2-6=9.6(cm2)
导学四
知识点讲解例题
1.B
解析:因为原来是由两个完全一样的三角形重叠在一起而形成的图形,故两个三角形的面积是相等的,那么两个三角形同 时减去重叠部分的面积,剩下部分的面积相等。一个三角形剩下的部分是梯形,一个三角形剩下的部分是阴影部分,求 阴影部分的面积就相当于求梯形的面积则有(10-3+10)×5÷2=42.5(cm2)
2.5
解析:连接BD,则三角形EAD与三角形EBD面积相等;三角形FDB与三角形FCB面积相等,则阴影部分的面积是整个四边形面 积的一半,即:10÷2=5
我爱展示
1.A
解析:长方形和平行四边形是等底等高的,因此长方形和正方形的面积相等,图中空白部分是长方形和平行四边形重合的 部分,面积也相等,长方形和平行四边形同时减去空白部分,所剩下的阴影部分的面积也相等。
2.18cm2
解析:6×(6+4)=60(cm2),60-6×6÷2-(4+6)×4÷2-(6-4)×4÷2=18(cm2)
将整个图形补成一个大长方形,然后用大长方形的面积减去三个三角形的面积,所得结果即为阴影部分的面积
限时考场模拟
1.3cm2
解析:(5+4)×6÷2=27(cm2), 4×6=24(cm2),27-24=3(cm2)
求甲乙面积的差,与大三角形的面积减去长方形的面积相等。因为大三角形的面积=甲的面积+空白部分的面积 ,长方形
的面积=乙的面积+空白部分的面积,二者相减,则空白部分相抵消,就是甲乙面积差。2.135cm2
解析:15×18÷2=135(cm2) 3.36cm2
解析:(10-2+10)×4÷2=36(cm2)
因为最初两个梯形的面积相等,它们重合的部分也相等,即空白部分,所以阴影部分的面积就和下面小直角梯形的面积 相等。
课后作业
1.错
解析:面积和周长的单位不同,所表示的意义也不同,即使求出来的数值相等,两者也是不可以比较的。2.错
解析:并不是任意两个三角形都可以拼成梯形的3.20平方厘米
解析:2×2÷1=4(cm),10×4÷2=20(cm2) 4.10
解析:三角形AFG的面积为AF×DG÷2,三角形CEG的面积CE×CG÷2 阴影部分的面积:AF×DG÷2+CE×CG÷2
=AF×(DG+GC)÷2
=AF×DC÷2
=2×10÷2
=10 (cm2)
5.19平方厘米
解析:用整个图形的面积:两个正方形的面积和减去空白部分三个三角形的面积,即为阴影部分的面积。解答过程:81÷9=9(cm),(9+6)×9÷2+9×(9-6)÷2+6×6÷2=99(cm2),6×6+81-99=18(cm2) 6.4厘米
解析:阴影部分的面积与三角形ADH的面积差与平行四边形BCEF和三角形ABC的面积差相等。解:设AH长为Xcm。
8×(10-X)-8×10÷2=8
80-8X-40=8
40-8X=8
8X=32 X=4
或三角形ABC的面积:8×10÷2=40(cm2)
平行四边形比三角形的面积多8 cm2则平行四边形的面积40+8=48(cm2) 则CH的长度为48÷8=6(cm),故AH的长度为10-6=4(cm)
