人教版数学七年级上册1.2.4.2有理数比较大小课件(33张)
文档属性
| 名称 | 人教版数学七年级上册1.2.4.2有理数比较大小课件(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
有理数大小的比较
1.写出下列各数的绝对值.
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0.
正数的绝对值是它本身
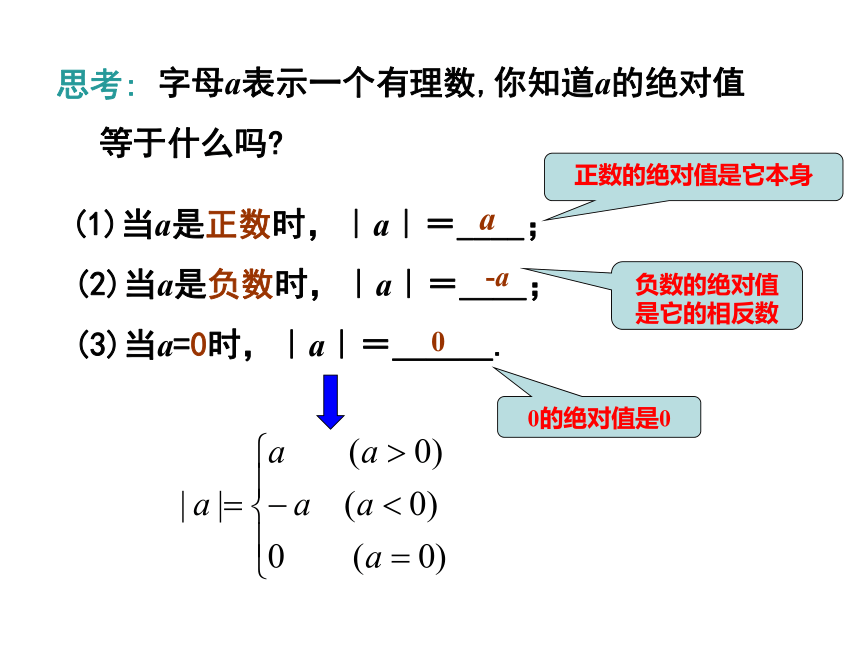
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
思考:
字母a表示一个有理数,你知道a的绝对值等于什么吗?
绝对值小于2的整数一共有多少个?
绝对值小于2的整数一共有3个,
它们分别是-1,1,0.
想一想
1)
绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
(1)绝对值等于0的数是___,
(2)绝对值等于5.25的正数是_____,
(3)绝对值等于5.25的负数是______,
(4)绝对值等于2的数是_______.
(5)绝对值最小的数是_______.
0
5.25
-5.25
2或-2
例2
填一填
易错提醒:
注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗漏负值.
0
下图表示某一天我国5个城市的最低气温.
武汉5
℃
北京-10℃ 上海0℃
广州10℃
哈尔滨-20℃
问:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
在数轴上表示的两个数,右边的数总比左边的数大.
小
大
-3
-2
-1
0
1
2
3
有理数大小的比较方法:
负数
0
正数
<
<
(1)8____6
(2)
2.3265___2.3266
(3)0.3___
(4)0.02___0
(5)
___
小学时学过比较数的大小吗?怎样比较的?
绝对值大的大
正数大于0
通分后根据同分母比较
先比整数部分再比小数部分
分数与小数互化比较
>
<
<
>
>
两个正数,绝对值大的较大,正数大于0.
1.用“>”或“<”号填空,并说明理由.
(1)3.5
0
(2)-2.8
0
(3)
0
0.1
(4)0
-4
(5)
-1.95
1.59
(6)3
-7
<
<
<
>
>
>
正数大于0,负数小于0,正数大于负数.
适用于一个数和0的大小比较,以及异号两数的大小比较.
同号两数怎样比较大小呢?
同正
同负
做一做
(
1
)在数轴上表示下列各数,并比较它们的大小;
-
1.5
,
-
3
,
-
1
,
-
5
(
2
)
求出(1)中各数的绝对值,并比较它们的大小;
(
3
)你发现了什么?
解:(1)
-
5
<
-
3
<-
1.5
<
-
1
(2)|
-1.5
|
=
1.5
;
|
-
3
|
=
3;
|
-1
|
=
1
;
|
-
5
|
=
5.
(3)由以上知:两个负数比较大小,绝对值大的反而小。
1
<
1.5
<3
<5
解法一(利用绝对值比较两个负数的大小)
解:
(1)因为|
-1|
=
1,|
-5
|
=
5
,1﹤5,
所以
-
1>
-
5
例2.
比较下列每组数的大小
(1)
-1和
–
5;
(2)-
和-
2.7
(2)因为|
-
|
=
,|-
2.7|
=2.7,
﹤2.7,所以
-
﹥-2.7
解法二
(利用数轴比较两个负数的大小)
(2)
解:(1)
因为-
2.7在
-
的左边,所以-
2.7﹤-
因为-
5在
–1左边,所以
-
5﹤
-
1
(1)正数大于0,0大于负数,正数大于负数;
(2)
两个负数,绝对值大的反而小.
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5___-7
-2___0
2____0
再次观察下列数,现在你会比较它们的大小吗?
>
>
<
>
用“<”,“>”,“=”连接下面的数.
3___-4;
5___0;
-7
___0;
-3
___-|-3|;
-|-7|
___0;
|2|
___-2.
练一练
<
>
=
>
>
<
6.将下列这些数按从小到大的顺序排列,并用<连接.
0;-3,|5|,-(-4),-|-5|.
-|-5|<
-3
<0<
-(-4)<|5|.
解:
(1)
和
(2)
和
-1.42
自学课本第13页例题中第(2)题的格式比较下列各对数的大小:
两个负数比较大小的一般步骤:
①求绝对值;
②比较绝对值的大小;
③比较负数的大小.
利用数轴把下列各数按由小到大的顺序排列:
-4,
+2,
-1.5,
0,
-3.5,
2.8
-4
●
-3.5
●
-1.5
●
0
●
+2
●
2.8
●
所以:
-4
<
-3.5
<
-1.5
<
0
<
+2
<
2.8
-4
-3
-2
-1
0
1
2
3
解:
利用数轴比较有理数大小的一般步骤:
①画数轴;②描点;③有序排列;④不等号连接.
零作为一个特殊的数,有它特殊的属性:
绝对值最小的数、相反数是它本身、绝对值是它本身.
有理数比较大小的方法:
方法1.数轴上表示的两个数,右边的总比左边的大;
方法2.正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小
.
1、比较下列各组数的大小,并说明你所运用的法则:
2___0
,
0___-8.3
,
2.5___-90
(2)-5__-3
,
-3.14__
-
,
-7.8__
-7.7
(3)-(-9)__-(+9)
,
-
[-(-0.3)]
__
-|-0.29|
>
>
>
<
<
>
>
<
随堂练习
1.下列说法正确的是( )
A.有理数的绝对值一定是正数
B.如果两个数的绝对值相等,那么这两个数相等
C.符号相反且绝对值相等的数互为相反数
D.一个数的绝对值越大,表示它的点在数轴上离原点越近
C
2.若|a|+
|b-3|
=0.则a
=_____,
b=
_____.
3.如果一个数的绝对值等于4.53
,则这个数是_______________.
4.如果|x-1|=2,则x=__________.
5.如果a
的相反数是-0.86,那么|a|
=______.
0
3
4.53或-4.53
3或-1
0.86
1.什么叫绝对值?你能根据绝对值的意义
得到什么?
2.怎样利用绝对值比较两数的大小?
3.通过本节课的学习,你还有什么疑惑?
4.0是一个特殊的数,它有什么特殊的性
质?
小结:
绝对值
:在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值.
(1.
几何定义)
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0
的绝对值是
0.
(2.代数定义)
会利用绝对值比较两个负数的大小:
两个负数,绝对值大的反而小.
人生的价值,并不是用时间,而是用深度去衡量的。
——列夫·托尔斯泰
8.已知|x-4|
+
|1-y|
=0,求3x+4y
的值.
解:
因为
|x-4|
+
|1-y|
=0,
所以
x-4=0,
1-y=0.
所以
x=4,
y=1.
所以
3x+4y
=3×4+4×1=16.
课前小测
1、绝对值等于3的数有
_________个,它们是_________。
2、若│x│=4,则x=______,若│x-5│=0,则x=_________.
3、绝对值小于5但大于2的整数是_________.
4、(1)、若│x-3│+
│y+5│=0,求
x+y=
_________
5、已知|x|=3,|y|=4,求x+y的值。
有理数大小的比较
1.写出下列各数的绝对值.
一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
0的绝对值是0.
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___.
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
思考:
字母a表示一个有理数,你知道a的绝对值等于什么吗?
绝对值小于2的整数一共有多少个?
绝对值小于2的整数一共有3个,
它们分别是-1,1,0.
想一想
1)
绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
(1)绝对值等于0的数是___,
(2)绝对值等于5.25的正数是_____,
(3)绝对值等于5.25的负数是______,
(4)绝对值等于2的数是_______.
(5)绝对值最小的数是_______.
0
5.25
-5.25
2或-2
例2
填一填
易错提醒:
注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗漏负值.
0
下图表示某一天我国5个城市的最低气温.
武汉5
℃
北京-10℃ 上海0℃
广州10℃
哈尔滨-20℃
问:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
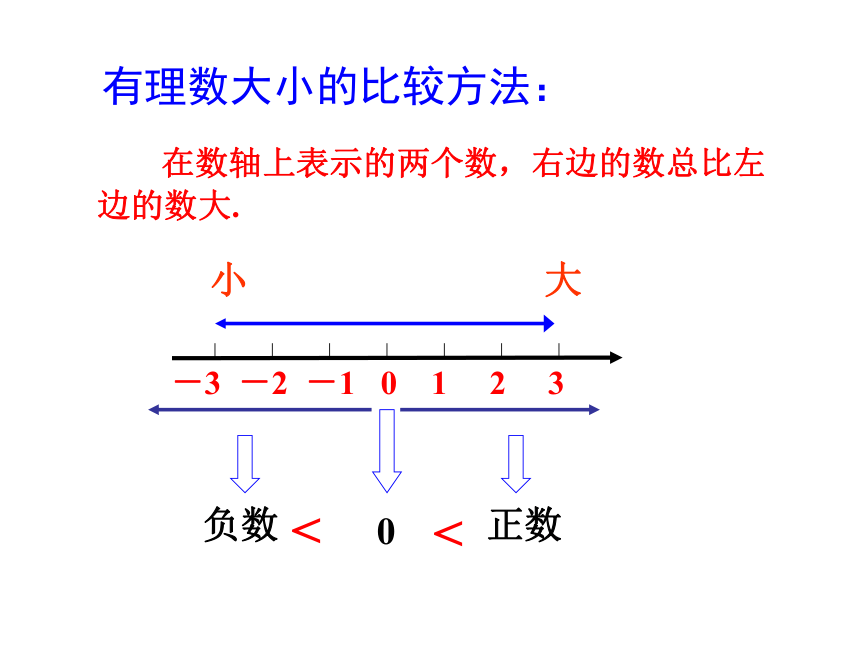
在数轴上表示的两个数,右边的数总比左边的数大.
小
大
-3
-2
-1
0
1
2
3
有理数大小的比较方法:
负数
0
正数
<
<
(1)8____6
(2)
2.3265___2.3266
(3)0.3___
(4)0.02___0
(5)
___
小学时学过比较数的大小吗?怎样比较的?
绝对值大的大
正数大于0
通分后根据同分母比较
先比整数部分再比小数部分
分数与小数互化比较
>
<
<
>
>
两个正数,绝对值大的较大,正数大于0.
1.用“>”或“<”号填空,并说明理由.
(1)3.5
0
(2)-2.8
0
(3)
0
0.1
(4)0
-4
(5)
-1.95
1.59
(6)3
-7
<
<
<
>
>
>
正数大于0,负数小于0,正数大于负数.
适用于一个数和0的大小比较,以及异号两数的大小比较.
同号两数怎样比较大小呢?
同正
同负
做一做
(
1
)在数轴上表示下列各数,并比较它们的大小;
-
1.5
,
-
3
,
-
1
,
-
5
(
2
)
求出(1)中各数的绝对值,并比较它们的大小;
(
3
)你发现了什么?
解:(1)
-
5
<
-
3
<-
1.5
<
-
1
(2)|
-1.5
|
=
1.5
;
|
-
3
|
=
3;
|
-1
|
=
1
;
|
-
5
|
=
5.
(3)由以上知:两个负数比较大小,绝对值大的反而小。
1
<
1.5
<3
<5
解法一(利用绝对值比较两个负数的大小)
解:
(1)因为|
-1|
=
1,|
-5
|
=
5
,1﹤5,
所以
-
1>
-
5
例2.
比较下列每组数的大小
(1)
-1和
–
5;
(2)-
和-
2.7
(2)因为|
-
|
=
,|-
2.7|
=2.7,
﹤2.7,所以
-
﹥-2.7
解法二
(利用数轴比较两个负数的大小)
(2)
解:(1)
因为-
2.7在
-
的左边,所以-
2.7﹤-
因为-
5在
–1左边,所以
-
5﹤
-
1
(1)正数大于0,0大于负数,正数大于负数;
(2)
两个负数,绝对值大的反而小.
负数和负数
正数和负数
负数和0
正数和0
-6___-8
5___-7
-2___0
2____0
再次观察下列数,现在你会比较它们的大小吗?
>
>
<
>
用“<”,“>”,“=”连接下面的数.
3___-4;
5___0;
-7
___0;
-3
___-|-3|;
-|-7|
___0;
|2|
___-2.
练一练
<
>
=
>
>
<
6.将下列这些数按从小到大的顺序排列,并用<连接.
0;-3,|5|,-(-4),-|-5|.
-|-5|<
-3
<0<
-(-4)<|5|.
解:
(1)
和
(2)
和
-1.42
自学课本第13页例题中第(2)题的格式比较下列各对数的大小:
两个负数比较大小的一般步骤:
①求绝对值;
②比较绝对值的大小;
③比较负数的大小.
利用数轴把下列各数按由小到大的顺序排列:
-4,
+2,
-1.5,
0,
-3.5,
2.8
-4
●
-3.5
●
-1.5
●
0
●
+2
●
2.8
●
所以:
-4
<
-3.5
<
-1.5
<
0
<
+2
<
2.8
-4
-3
-2
-1
0
1
2
3
解:
利用数轴比较有理数大小的一般步骤:
①画数轴;②描点;③有序排列;④不等号连接.
零作为一个特殊的数,有它特殊的属性:
绝对值最小的数、相反数是它本身、绝对值是它本身.
有理数比较大小的方法:
方法1.数轴上表示的两个数,右边的总比左边的大;
方法2.正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小
.
1、比较下列各组数的大小,并说明你所运用的法则:
2___0
,
0___-8.3
,
2.5___-90
(2)-5__-3
,
-3.14__
-
,
-7.8__
-7.7
(3)-(-9)__-(+9)
,
-
[-(-0.3)]
__
-|-0.29|
>
>
>
<
<
>
>
<
随堂练习
1.下列说法正确的是( )
A.有理数的绝对值一定是正数
B.如果两个数的绝对值相等,那么这两个数相等
C.符号相反且绝对值相等的数互为相反数
D.一个数的绝对值越大,表示它的点在数轴上离原点越近
C
2.若|a|+
|b-3|
=0.则a
=_____,
b=
_____.
3.如果一个数的绝对值等于4.53
,则这个数是_______________.
4.如果|x-1|=2,则x=__________.
5.如果a
的相反数是-0.86,那么|a|
=______.
0
3
4.53或-4.53
3或-1
0.86
1.什么叫绝对值?你能根据绝对值的意义
得到什么?
2.怎样利用绝对值比较两数的大小?
3.通过本节课的学习,你还有什么疑惑?
4.0是一个特殊的数,它有什么特殊的性
质?
小结:
绝对值
:在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值.
(1.
几何定义)
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0
的绝对值是
0.
(2.代数定义)
会利用绝对值比较两个负数的大小:
两个负数,绝对值大的反而小.
人生的价值,并不是用时间,而是用深度去衡量的。
——列夫·托尔斯泰
8.已知|x-4|
+
|1-y|
=0,求3x+4y
的值.
解:
因为
|x-4|
+
|1-y|
=0,
所以
x-4=0,
1-y=0.
所以
x=4,
y=1.
所以
3x+4y
=3×4+4×1=16.
课前小测
1、绝对值等于3的数有
_________个,它们是_________。
2、若│x│=4,则x=______,若│x-5│=0,则x=_________.
3、绝对值小于5但大于2的整数是_________.
4、(1)、若│x-3│+
│y+5│=0,求
x+y=
_________
5、已知|x|=3,|y|=4,求x+y的值。
