苏科版八年级数学上册 第一章全等三角形 培优测试卷(Word版 无答案)
文档属性
| 名称 | 苏科版八年级数学上册 第一章全等三角形 培优测试卷(Word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 154.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 10:22:38 | ||
图片预览



文档简介
八年级数学上册
第一章全等三角形
培优测试卷
总分:120分
时间:90分钟
选择题(每题3分,共24分)
1.下列各组图形中,是全等三角形的是( )
A.两个含70°角的直角三角形
B.斜边对应相等的两个等腰直角三角形
C.边长分别为3和4的两个等腰三角形
D.腰长相等的两个等腰三角形
2.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE
B.∠BAD=∠CAE
C.AB=AE
D.∠ABC=∠AED
3.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,
∠CAD=25°,则∠ABE的度数为( )
A.30°
B.15°
C.25°
D.20°
(第2题图)
(第3题图)
(第4题图)
(第5题图)
4.如图,请你根据所学的知识,说明作出∠A'O'B'=∠AOB的依据是( )
A.SAS
B.ASA
C.AAS
D.SSS
5.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=14cm,BC=16cm,则DE的长度为( )
A.1cm
B.2cm
C.3cm
D.4cm
6.如图,在△ABC中,CD是∠C的外角平分线,P是CD上异于C的任意一点,设PB=m,PA=n,BC=a,AC=b,则(m+n)与(a+b)的大小关系是( )
A.m+n>a+b
B.m+n<a+b
C.m+n=a+b
D.无法确定
7.已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20
B.40
C.60
D.100
(第6题图)
(第7题图)
(第8题图)
8.如图,在△ABC中,P、Q分别是BC、AC上的点,作PD⊥AB,PE⊥AC,垂足分别为D、E,若AQ=PQ,PD=PE,则下列结论:①AE=AD;②∠B=∠C;③QP∥AD;④∠BAP=∠CAP;⑤△ABP≌△ACP.其中正确的有( )
A.①③④
B.①②⑤
C.①②③④
D.①②③④⑤
二.填空题(每题3分,共30分)
9.如图所示,AC=DB,若想证明∠ACB=∠DBC,需要证明∠ACB与∠DBC所在的三角形全等,即△ABC≌△DCB,则还需要添加的条件是
.
10.如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D=
°.
11.如图是由九个边长为1的小正方形拼成的大正方形,求图中∠1+∠2+∠3+∠4+∠5的和的度数为
.
(第9题图)
(第10题图)
(第11题图)
(第12题图)
12.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=25°,则∠3=
.
13.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,则∠BDC=
.
14.已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=
.
(第13题图)
(第14题图)
(第15题图)
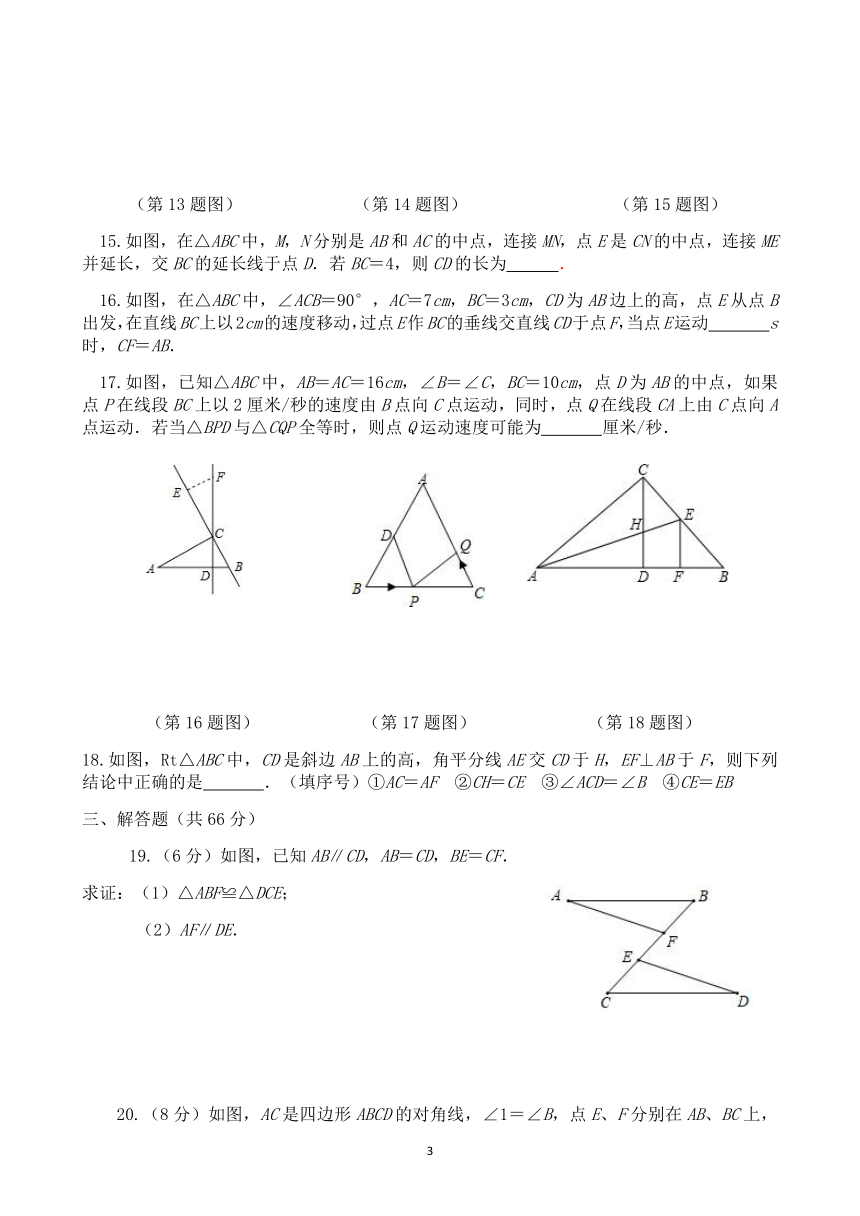
15.如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为
.
16.如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高,点E从点B出发,在直线BC上以2cm的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动
s时,CF=AB.
17.如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若当△BPD与△CQP全等时,则点Q运动速度可能为
厘米/秒.
(第16题图)
(第17题图)
(第18题图)
18.如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中正确的是
.(填序号)①AC=AF
②CH=CE
③∠ACD=∠B
④CE=EB
三、解答题(共66分)
19.(6分)如图,已知AB∥CD,AB=CD,BE=CF.
求证:(1)△ABF≌△DCE;
(2)AF∥DE.
20.(8分)如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
21.(8分)如图,在△ABC和△DBE中,点D在边AC上,BC与DE交于点P,AB=DB,
∠A=∠BDE,∠ABD=∠CBE.
(1)求证:BC=BE;
(2)若AD=DC=2.5,BC=4,求△CDP与△BEP的周长之和.
22.(8分)如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F.
(1)求证:△ABE≌△CAD;
(2)如果∠ABC=65°,∠ABE=25°,求∠D的度数.
23.(8分)阅读材料并完成习题:
在数学中,我们会用“截长补短”的方法来构造全等三角形解决问题.请看这个例题:如图1,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若AC=2cm,求四边形ABCD的面积.
解:延长线段CB到E,使得BE=CD,连接AE,我们可以证明△BAE≌△DAC,根据全等三角形的性质得AE=AC=2,∠EAB=∠CAD,则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°,得S四边形ABCD=S△ABC+S△ADC=SABC+SABE=S△AEC,这样,四边形ABCD的面积就转化为等腰直角三角形EAC面积.
(1)根据上面的思路,我们可以求得四边形ABCD的面积为
cm2.
(2)请你用上面学到的方法完成下面的习题.
如图2,已知FG=FN=HM=GH+MN=2cm,∠G=∠N=90°,求五边形FGHMN的面积.
24.(8分)已知,在△ABC中,AC=BC.分别过A,B点作互相平行的直线AM和BN.过点C的直线分别交直线AM,BN于点D,E.
(1)如图1.若CD=CE.求∠ABE的大小;
(2)如图2.∠ABC=∠DEB=60°.求证:AD+DC=BE.
25.(10分)如图1,CA=CB,CD=CE,∠ACB=∠DCE=α
(1)求证:BE=AD;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
26.(10分)如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
第一章全等三角形
培优测试卷
总分:120分
时间:90分钟
选择题(每题3分,共24分)
1.下列各组图形中,是全等三角形的是( )
A.两个含70°角的直角三角形
B.斜边对应相等的两个等腰直角三角形
C.边长分别为3和4的两个等腰三角形
D.腰长相等的两个等腰三角形
2.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE
B.∠BAD=∠CAE
C.AB=AE
D.∠ABC=∠AED
3.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,
∠CAD=25°,则∠ABE的度数为( )
A.30°
B.15°
C.25°
D.20°
(第2题图)
(第3题图)
(第4题图)
(第5题图)
4.如图,请你根据所学的知识,说明作出∠A'O'B'=∠AOB的依据是( )
A.SAS
B.ASA
C.AAS
D.SSS
5.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=14cm,BC=16cm,则DE的长度为( )
A.1cm
B.2cm
C.3cm
D.4cm
6.如图,在△ABC中,CD是∠C的外角平分线,P是CD上异于C的任意一点,设PB=m,PA=n,BC=a,AC=b,则(m+n)与(a+b)的大小关系是( )
A.m+n>a+b
B.m+n<a+b
C.m+n=a+b
D.无法确定
7.已知△ABC≌△A'B'C,∠A=40°,∠CBA=60°,A'C交边AB于P(点P不与A、B重合).BO、CO分别平分∠CBA,∠BCP,若m°<∠BOC<n°,则n﹣m的值为( )
A.20
B.40
C.60
D.100
(第6题图)
(第7题图)
(第8题图)
8.如图,在△ABC中,P、Q分别是BC、AC上的点,作PD⊥AB,PE⊥AC,垂足分别为D、E,若AQ=PQ,PD=PE,则下列结论:①AE=AD;②∠B=∠C;③QP∥AD;④∠BAP=∠CAP;⑤△ABP≌△ACP.其中正确的有( )
A.①③④
B.①②⑤
C.①②③④
D.①②③④⑤
二.填空题(每题3分,共30分)
9.如图所示,AC=DB,若想证明∠ACB=∠DBC,需要证明∠ACB与∠DBC所在的三角形全等,即△ABC≌△DCB,则还需要添加的条件是
.
10.如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D=
°.
11.如图是由九个边长为1的小正方形拼成的大正方形,求图中∠1+∠2+∠3+∠4+∠5的和的度数为
.
(第9题图)
(第10题图)
(第11题图)
(第12题图)
12.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=25°,则∠3=
.
13.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,则∠BDC=
.
14.已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=
.
(第13题图)
(第14题图)
(第15题图)
15.如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为
.
16.如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高,点E从点B出发,在直线BC上以2cm的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动
s时,CF=AB.
17.如图,已知△ABC中,AB=AC=16cm,∠B=∠C,BC=10cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若当△BPD与△CQP全等时,则点Q运动速度可能为
厘米/秒.
(第16题图)
(第17题图)
(第18题图)
18.如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中正确的是
.(填序号)①AC=AF
②CH=CE
③∠ACD=∠B
④CE=EB
三、解答题(共66分)
19.(6分)如图,已知AB∥CD,AB=CD,BE=CF.
求证:(1)△ABF≌△DCE;
(2)AF∥DE.
20.(8分)如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
21.(8分)如图,在△ABC和△DBE中,点D在边AC上,BC与DE交于点P,AB=DB,
∠A=∠BDE,∠ABD=∠CBE.
(1)求证:BC=BE;
(2)若AD=DC=2.5,BC=4,求△CDP与△BEP的周长之和.
22.(8分)如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F.
(1)求证:△ABE≌△CAD;
(2)如果∠ABC=65°,∠ABE=25°,求∠D的度数.
23.(8分)阅读材料并完成习题:
在数学中,我们会用“截长补短”的方法来构造全等三角形解决问题.请看这个例题:如图1,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若AC=2cm,求四边形ABCD的面积.
解:延长线段CB到E,使得BE=CD,连接AE,我们可以证明△BAE≌△DAC,根据全等三角形的性质得AE=AC=2,∠EAB=∠CAD,则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°,得S四边形ABCD=S△ABC+S△ADC=SABC+SABE=S△AEC,这样,四边形ABCD的面积就转化为等腰直角三角形EAC面积.
(1)根据上面的思路,我们可以求得四边形ABCD的面积为
cm2.
(2)请你用上面学到的方法完成下面的习题.
如图2,已知FG=FN=HM=GH+MN=2cm,∠G=∠N=90°,求五边形FGHMN的面积.
24.(8分)已知,在△ABC中,AC=BC.分别过A,B点作互相平行的直线AM和BN.过点C的直线分别交直线AM,BN于点D,E.
(1)如图1.若CD=CE.求∠ABE的大小;
(2)如图2.∠ABC=∠DEB=60°.求证:AD+DC=BE.
25.(10分)如图1,CA=CB,CD=CE,∠ACB=∠DCE=α
(1)求证:BE=AD;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
26.(10分)如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
