人教版七年级上册第四章 图形认识初步整章讲学稿(精品学案)
文档属性
| 名称 | 人教版七年级上册第四章 图形认识初步整章讲学稿(精品学案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-12 00:00:00 | ||
图片预览


文档简介
几何图形
一、学习目标
1.通过观察生活中的大量图片或实物,体验、感受、认识以生活中的事物为原型的几何图形;
2.认识一些简单几何体(长方体、正方体、棱柱、棱锥、圆柱、圆锥、球等)的基本特性;
3.能识别这些几何体.
二、学习过程
(一)自主学习:阅读课文P116-118,完成下列问题:
⑴ 对于生活中各种各样的物体,数学(几何学)关注的是它们的 、 、 。
⑵ 常见的立体图形有:
⑶ 常见的平面图形有: 。
⑷ 立体图形与平面图形的区别:
尝试应用
1.如下图所示,这些物体所对应的立体图形分别是: .
2.下列几种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;.其中属于立体图形的是( )
A. ①②③; B. ③④⑤; C. ③⑤; D.④⑤
3.图中的一些物体与我们学过的哪些图形相类似?把相应的物体和图形连接起来
例 看一看、想一想:说说圆柱、棱柱、圆锥、棱锥的异同
1、下列立方体图形有9个面的是 ( )
A、六棱锥 B、八棱锥 C、六棱柱 D、八棱柱
2.如图,左面的几何体叫三棱柱,它有五个面,9条棱,6个顶点,中间和右边的几何体分别是四棱柱和五棱柱。
(1)四棱柱有 个顶点, 条棱, 个面;
(2)五棱柱有 个顶点, 条棱, 个面;
(3)你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
(4)那么n棱柱呢?
几何图形(2)----立体图形的三视图
一、学习目标
1.经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果,了解为什么要从不同方向看.
2.能画出从不同方向看一些基本几何体(直棱柱、圆柱、圆锥、球)以及它们的简单组合得到的平面图形
二、学习过程:
苏东坡《题西林壁》:横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中。从数学的角度看:这首诗中蕴含何数学道理?
从不同方位看立体图形得到的图形一般是 的.
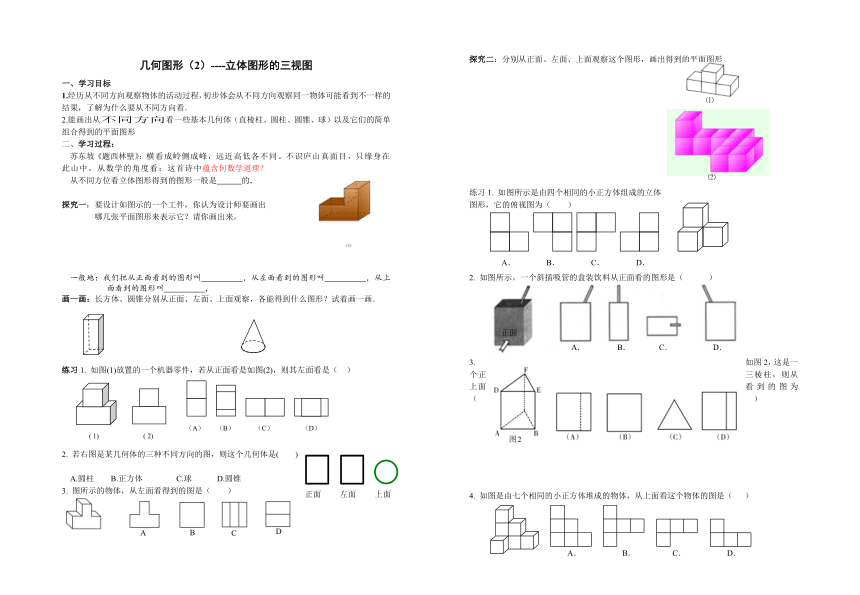
探究一:要设计如图示的一个工件,你认为设计师要画出
哪几张平面图形来表示它?请你画出来。
一般地:我们把从正面看到的图形叫 ,从左面看到的图形叫 ,从上面看到的图形叫 ,
画一画:长方体、圆锥分别从正面、左面、上面观察,各能得到什么图形?试着画一画.
练习1. 如图(1)放置的一个机器零件,若从正面看是如图(2),则其左面看是( )
2. 若右图是某几何体的三种不同方向的图,则这个几何体是( )
A.圆柱 B.正方体 C.球 D.圆锥
3. 图所示的物体,从左面看得到的图是( )
探究二:分别从正面、左面、上面观察这个图形,画出得到的平面图形
练习1. 如图所示是由四个相同的小正方体组成的立体
图形,它的俯视图为( )
2. 如图所示,一个斜插吸管的盒装饮料从正面看的图形是( )
3. 如图2,这是一个正三棱柱,则从上面看到的图为( )
4. 如图是由七个相同的小正方体堆成的物体,从上面看这个物体的图是( )
几何图形(3)----立体图形的平面展开图
一、学习目标
1.能直观认识立体图形和展开图,了解研究立体图形方法。
2.通过观察和动手操作,经历和体验平面图形和立体图形相互转换的过程,培养动手操作能力,初步建立空间观念,发展几何直觉。
二、学习过程:
问题:生活中,很多商品的包装盒都是长方体、圆柱体、圆锥等等,如何制作这些形状的纸制包装盒呢?
回顾复习:
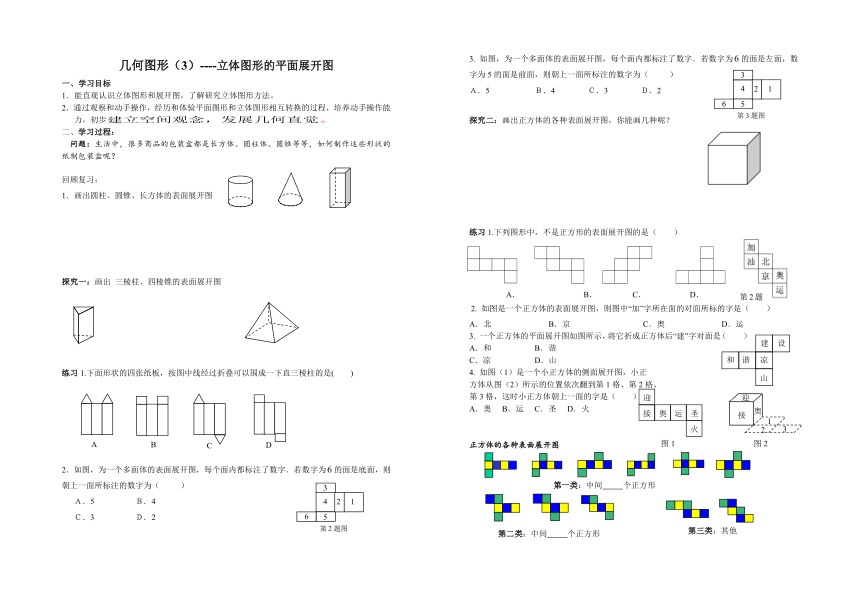
1.画出圆柱、圆锥、长方体的表面展开图
探究一:画出 三棱柱、四棱锥的表面展开图
练习1.下面形状的四张纸板,按图中线经过折叠可以围成一下直三棱柱的是( )
2.如图,为一个多面体的表面展开图,每个面内都标注了数字.若数字为的面是底面,则朝上一面所标注的数字为( )
A.5 B.4
C.3 D.2
3. 如图,为一个多面体的表面展开图,每个面内都标注了数字.若数字为的面是左面,数字为5的面是前面,则朝上一面所标注的数字为( )
A.5 B.4 C.3 D.2
探究二:画出正方体的各种表面展开图,你能画几种呢?
练习1.下列图形中,不是正方形的表面展开图的是( )
A. B. C. D.
2. 如图是一个正方体的表面展开图,则图中“加”字所在面的对面所标的字是( )
A.北 B.京 C.奥 D.运
3. 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐
C.凉 D.山
4. 如图(1)是一个小正方体的侧面展开图,小正
方体从图(2)所示的位置依次翻到第1格、第2格、
第3格,这时小正方体朝上一面的字是( )
A.奥 B.运 C.圣 D.火
正方体的各种表面展开图
点、线、面、体
一、学习目标
(1)了解几何体、平面和曲面的意义,能正确判定围成几何体的面是平面还是曲面; ( http: / / )
(2)了解几何图形构成的基本元素是点、线、面、体及其关系,能正确判定由点、线、面、体经过运动变化形成的简单的几何图形.
二、学习过程:
复习:如右图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 块小正方体;
(2)请在下面分别画出它的主视图、左视图和俯视图.
问题:
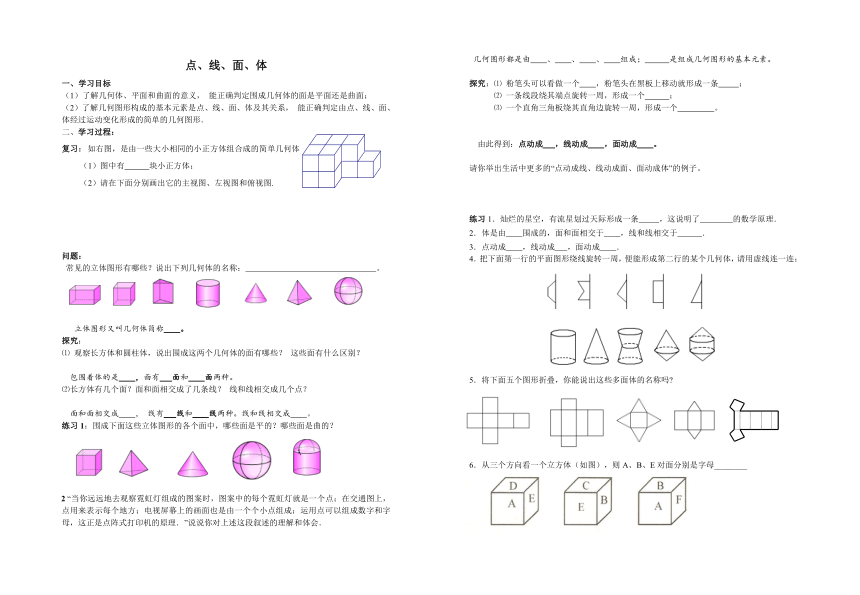
常见的立体图形有哪些?说出下列几何体的名称: 。
立体图形又叫几何体简称 。
探究:
⑴ 观察长方体和圆柱体,说出围成这两个几何体的面有哪些?这些面有什么区别?
包围着体的是 ,面有 面和 面两种。
⑵长方体有几个面?面和面相交成了几条线?线和线相交成几个点?
面和面相交成 , 线有 线和 线两种。线和线相交成 。
练习1:围成下面这些立体图形的各个面中,哪些面是平的?哪些面是曲的?
2 “当你远远地去观察霓虹灯组成的图案时,图案中的每个霓虹灯就是一个点;在交通图上,点用来表示每个地方;电视屏幕上的画面也是由一个个小点组成;运用点可以组成数字和字母,这正是点阵式打印机的原理.”说说你对上述这段叙述的理解和体会.
几何图形都是由 、 、 、 组成; 是组成几何图形的基本元素。
探究:⑴ 粉笔头可以看做一个 ,粉笔头在黑板上移动就形成一条 ;
⑵ 一条线段绕其端点旋转一周,形成一个 ;
⑶ 一个直角三角板绕其直角边旋转一周,形成一个 。
由此得到:点动成 ,线动成 ,面动成 。
请你举出生活中更多的“点动成线、线动成面、面动成体”的例子。
练习1.灿烂的星空,有流星划过天际形成一条 ,这说明了 的数学原理.
2.体是由 围成的,面和面相交于 ,线和线相交于 .
3.点动成 ,线动成 ,面动成 .
4.把下面第一行的平面图形绕线旋转一周,便能形成第二行的某个几何体,请用虚线连一连:
5.将下面五个图形折叠,你能说出这些多面体的名称吗
6.从三个方向看一个立方体(如图),则A、B、E对面分别是字母________
直线、射线、线段(1)
学习目标
1、认识直线、射线、线段及它们的联系和区别,掌握它们的表示方法;2、了解“两点确定一条直线”的性质;3、能根据语句画出相应的图形,会用语句描述简单的图形。
学习过程]
一、导入新课
我们知道,点是几何研究的最基本的图形,点动成线,线有直线、射线和线段。今天我们就来学习这些简单的几何图形。
二、直线及其性质
探究:
如图①,要在墙上固定一根木条,
使它不能转动,至少需要几颗钉子?
(2)如下图,经过一点O画直线,能画出几条?经过点A、点B两点呢?
由此可得一个基本事实:
经过两点有 条直线,而且只有 条直线。简述为:两点确定一条直线。
你能再举几个这样的例子吗?
直线有两种表示方法:①用一个小写字母表示;②用两个大写字母表示。
平面上一个点与一条直线的位置有什么关系?
①点在直线上;②点在直线外。
一个点在一条直线上,也可以说这条直线经过这个点如图①,一个点不在一条直线上,也可以说这条直线不经过这个点,如图②。
当两条直线有一个共公点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
三、射线和线段
我们手中的直尺给我们线段的形象,手电筒发出的光给我们射线的形象,如图。显然,射线和线段都是直线的一部分。
图①中的线段记作线段AB或线段a;图②中的射线记作射线OA或射线m。
注意:用两个大写字母表示射线时,表示端点的字母一定要写在前面。
思考:直线、射线和线段有什么联系和区别?
性质与表法名称 端点 个数 能否度量 向几方延伸 图形 称呼与表示
直 线
射 线
线 段
四、应用新知
例 读下列语句,并按照语句画出图形:
(1)画线段AB(也叫连接AB);⑵直线经过A、B两点,点B在点A的左边;⑶直线AB、CD都经过点O,点E不在直线AB上,但在直线CD上。
解:
练习:1、植树时,要确定一行树的位置,只需确定这一行树中任两棵树的位置,其中体现的数学道理是______________________.
2、将线段一端延伸能得到______,将线段两端都延伸能得到______.
3、图中共有几条线段?几条射线?几条直线?能用字母表示出来的分别用字母表示出来。
4、如图,点C在直线AB______. 点O在直线BD______. O点是_______的交点. 过点A的直线共有_____条,它们是_________.
5、按下列语言作图
(1)连接AB、CD
(2)作直线AD
(3)作射线CB,交直线AD于点O
(4)过点O作一条直线,交线段AB
于点M,交线段CD于N.
直线、射线、线段(2)
学习目标:
1、会用尺规画一条线段等于已知线段;2、会比较两条线段的长短;3、理解线段中点的概念,了解“两点之间,线段最短”的性质。
学习过程:
一、问题导入
现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长?
上面的实际问题可以转化为下面的数学问题:
已知线段a,画一条线段等于已知线段a。
二、作一条线段等于已知线段
现在我们来解决这个问题。
作法:(1)
(2)
例1 已知线段a、b,求作线段AB=a+b
解:
做一做:作线段AB=a-b。
三、比较两条线段的长短
两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢?我们先来回答下面的问题。
怎样比较两个同学的身高?
一是: ;二是: 。
如果把两个同学看成两条线段,那么比较两条线段就有两种方法。
1、度量法:用刻度尺分别量出两条线段的长度从而进行比较。
2、叠合法:把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。
记作: AB CD AB CD AB CD
四、线段的中点及等分点
如图(1),点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点。
记作:AM=MB或AM=MB=AB或2AM=2MB=AB。
如图(2),点M、N把线段AB分成相等的三段AM、MN、NB,点M、N叫做线段AB的 等分点。类似地,还有四等分点,等等。
五、线段的性质
如图,从A地到B地有三条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线。
这说明了什么呢?
两点所连的线中,线段 。简单地说成:
两点之间,线段 。
连接两点间的线段的长度叫做这两点间的距离。
注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。
六、巩固练习
1.线段AB=8cm,C是AB的中点,D是BC的中点,A、D两点间的距离是_____cm.
2.如图3,在直线I上顺次取A、B、C、D四点,则AC=______+BC=AD-_____,AC+BD- BC=________.
3.下列语句准确规范的是( )
A. 直线a、b相交于一点m B. 延长直线AB
C. 反向延长射线AO(O是端点) D. 延长线段AB到C,使BC=AB
4.如果点C在AB上,下列表达式①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
5. 已知点C是线段AB的中点,点D是线段BC的中点,CD=2.5厘米,请你求出线段AB、AC、AD、BD的长各为多少?
6. 如图,DB=3cm,BC=7cm,C是AD的中点,求AB的长.
7.画线段AB=10mm,延长AB至C,使BC=15mm,再反向延长线段AB至D,使DA=15mm,先依题意画出图形,并求出DC的长
直线、射线、线段(3)
学习目标:
1、利用直线、线段的性质解决相关实际问题;
2、利用线段的中点定义解决相关计算问题.
学习过程:
复习:⑴某村庄和小学分别位于两条交叉的大路边,可是有些人不爱惜庄稼,
每年冬天麦田里总会走出一条小路来,其中的数学道理是________________________.
⑵读出下列语句,并按照语句画出图形.
① 点C在直线AB上,而点D在直线AB外; ② 直线AB和直线BC相交于B;
③ 经过点A的四条直线a,b,c,d; ④ 延长线段AB到C,使AC=3AB .
例1 已知线段AB=10㎝, C是线段AB上任意一点,E、F分别是AC、BC的中点,求线段EF的长?
练习1:⑴已知线段AB及一点P,若AP+PB=AB,则点P在
⑵. 已知C是线段AB上的一点,D是CB的中点,DB=2cm,AC=8cm,则AB=__ cm.
⑶ 如图,C、D是线段AB上的两点,且AC=CB,CD=DB,则线段AB的中点是点___,点D 是线段____的中点,AC=__DB,DB=__AB.
⑷ 已知线段AB=10, 点C在直线AB上,且AC=4,若点D是AB的中点,求DC的长.
例2 已知C、D是线段AB上的两点,且AC︰CD︰DB=2︰3︰4,E、F分别是AC、DB的中点,如果EF=12㎝,求线段AB的长?
【巩固练习】
⑴ 在同一个学校上学的小明、小伟、小红三位同学住在A、B、C三个住宅区,如图2所示,A、B、C三点共线,且AB=60米,BC=100米,他们打算合租一辆接送车去上学,由于车位紧张,准备在此之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在何处?
⑵线段AB=4cm,延长线段AB到C,使BC = 1cm,再反向延长AB到D,使AD=3 cm,E是AD中点,F是CD的中点,求EF的长度。
⑶ 将线段AB延长至C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8㎝,求AB的长?
角(1)
学习目标:
1、通过丰富的实例,理解角的形成,建立几何中角的概念,掌握角的两种定义形式和四种表示方法.
2、通过在图片、实例中找角,培养学生的观察、探究、抽象、概括的能力以及把实际问题转化为数学问题的能力。
学习过程:
一、提出问题(前几节课我们一起研究和讨论了线段,射线,直线的特点和性质,今天就来研究另一种图形——角)
⑴请你根据小学对角的认识与理解,画一个角。
⑵角的两边是 ;他们的位置关系如何?根据自己的理解试给角下一个定义?
探究:
(一)角的概念
角的定义:有 组成的图形叫做角.这个公共端点是角的 ,这两条射线是角的 .
举出几个生活中给我们角的形象的物体: 。
(二)角的表示方法:
在刚才的讨论中,我们发现了生活中有许多角的形象.那么,我们如何给这些角取名呢?
①用三个大写字母表示:∠AOB(顶点写在中间)
②用一个大写字母表示:∠O(用顶点表示,该顶点处只有一个角)
③用一个希腊字母表示:∠α(用小弧圈在图中表示)
④用数字表示:∠1(用小弧圈在图中表示)
例1 如图,回答下列问题。(1)写出图中能用一个字母表示的角;(2)写出以B为顶点的角;(3)图中共有几个角 分别把它们表示出来。
练习
1.如下左图所示,把图中用数子表示的角,改用大写字母表示分别是________ .
( http: / / www. / )
2.将上右图中的角用不同的方法表示出来,填入下表:
∠1 ∠3 ∠4
∠BCA ∠ABC
(三)用旋转观点定义角
角也可以看成是由一条射线绕着它的端点旋转而形成的图形.
当射线OA绕点O旋转时,当终止位置OB和起始位置OA成一条直线时,会形成什么角?继续旋转,当OB和OA重合时,又形成什么角?
① 绕着端点旋转到角的终边和始边成一直线,这时所成的角叫做 ;
② 绕着端点旋转到角的终边和始边再次重合,这时所成的角叫做 。
③ 小于180°角可以分成: 、 、 。
应用
1.把图中的角表示成下列形式,哪些正确,哪些不正确?
(1)∠APO (2)∠AOP (3)OPC (4)∠OCP
(5)∠O (6) ∠P
2.图中以O点为顶点的角有几个?以D点为顶点的角有几个?试用适当的方法来表示这些角。
巩固练习
1.下列说法错误的是( )
A.平角的一半是直角 B.平角的两倍是周角 C.锐角的两倍是钝角D.钝角的一半是锐角
2.下列说法正确的是
A. 角的两条边在同一条直线上的角是周角 B.五角星图形中有五个角
C. 18时整,时针和分针成一个平角 D.长方体表面上只有四个角
3.画射线OA,OB;在∠AOB的内部和外部分别画射线OC, OD.那么所画的图中有哪几个角?请用适当的方法表示这些角.
角的度量(2)
学习目标:
1、认识度、分、秒,会进行度、分、秒间单位互化及角的和、差、倍、分计算.
2、通过度、分、秒间的互化及角度的简单运算,经历利用已有知识解决新问题的探索过程.
学习过程:
复习回顾
任意画一个锐角和钝角,用字母分别表示这两个角,用量角器分别量出这两个角的度数。
探究新知:
角度制(阅读课文P137内容,完成下列填空)
我们常用量角器量角.在量角器中看到,把一个平角 等分,每一份就是 的角.记作1°
在实际生活中,有时还需要更精密的角度.因此我们把1度的角 等分,每份就是 的角,记作;把1分的角 等分,每份就是 的角,记作1".
角的度量:
1周角= 1平角= 1直角=
1°= 1′= 1°= ″
归纳:以度、分、秒为单位的角的度量制叫做 .
想一想:角度进位制和其他什么进位制相类似?
2、回顾两个问题:
问题① 3.32小时= 小时 分 秒; 问题② 12小时9分36秒= 小时;
例1 ⑴ 用度、分、秒表示48.12°;⑵ 用度表示50°7′30″;⑶= 度
例2 计算: ⑴ +; ⑵ ; ⑶ ×4
例3 把一个周角7等分,每一份是多少度的角?(精确到分)
练习
1.()°=_____′=_____″; 6000″=______′=_______°.
2.在钟表上,1点30分时,时针与分针所成的角是( ).
A.150° B.165° C.135° D.120°
3.下列各角中,不可能是钝角的角是( ).
A.周角 B.平角 C.钝角 D.直角
4.计算
(1)53°28′+47°32′; (2)17°50′-3°27′;
⑶ 48°39′+67°41′ ⑷ 90°-78°19′40″;
⑸ 15°24′×5; ⑹31°42′÷5(精确到1″).
角的比较与运算(1)
学习目标:
1、会比较角的大小,能估计一个角的大小.在操作活动中认识角的平分线;
2、实际观察、操作,体会角的大小,培养学生的观察思维能力;
学习过程:
复习回顾
如图(1),已知线段AB和线段CD,如何比较这两条线段的大小呢?
探究新知:
问题1:如图(2)已知∠ABC和∠DEF。请大家讨论一下,用什么方法可以比较这两个角的大小?
1、角的大小的比较方法:
;
。
2、角的和差.
观察下列图形,图中共有几个角?图中各角之间有怎样的和差关系?
① ∠AOB+∠BOC= ;② ∠AOC-∠AOB=
③∠AOC-∠AOB=________.
练习1:一副三角板,各角的度数分别是多少度?你能用一副三角板画出哪些度数的角?
问题2:在一张纸上画出一个角并剪下,将这个角对折,使其两边重合.想想看,折痕与角两边所成的两个角的大小有什么关系?
3.角的平分线
从一个角的顶点出发,把这个角分成 的两个角的射线,叫做这个角的平分线。类似的还有角的三等分线、四等分线等等.
⑴如果OC平分∠AOB,你能得到哪些结论?
⑵想一想,有什么方法可画出一个角的平分线呢?
画一画:按下列语句画图:
① 画一个∠AOB;② 在∠AOB的两边上分别取OC=OD=4cm;③ 连结CD;④ 作出CD的中点E;⑤ 画射线OE. 猜想OE与∠AOB的关系?
例1 如图,已知∠AOC=120°如果OB是∠AOC内任意射线,OE,OF分别是∠AOB,∠BOC的平分线.求:∠EOF的度数.
巩固练习
1.如果∠1=∠2,∠1+∠3=90°,则∠2+∠3=_______.
2.如图,有“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB-∠BOC; (2)∠AOC_______∠AOB;
(3)∠BOD-∠BOC______∠DOC; (4)∠AOB______∠AOC+∠BOD.
3.如图,OC平分∠AOB,OD平分∠AOC,
①图中相等的角有_______ ;
②∠AOD=______∠AOC=______∠AOB.
4.如下图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,
求∠AOB的度数.
角的比较与运算(2)
学习目标:
1、在具体情境中了解余角与补角.懂得等角的余角相等,等角的补角相等.并能运用这些性质解决一些简单的实际问题;
2、经历观察、操作、推理、交流等活动,发展学生的空间观念,培养学生的推理能力和有条理的表达能力;
学习过程:
复习:说出一副三角尺中各个角的度数:① 、② 。
探究新知:
余角与补角的概念(预习课文P141,完成下列填空)
⑴ 如果两个角的和等于 ( ),我们就说这两个角 ,简称互余。即其中一个角是另一个角的 .
例如:如果∠1+∠2=90°,那么∠1与∠2 ,∠1是 的余角,∠2也是∠1的
⑵ 如果两个角的和等于 度 ( ),就说这两个角 ,简称互补。即其中一个角是另一个角的 .
例如:如果∠1与∠2互补,那么∠1+∠2= ,
2、余角与补角的性质
问题1:如果∠1与∠2互余,∠3与∠4互余,并且∠1=∠3,那么∠2与∠4相等吗?为什么?
问题2:如果∠1与∠2互补,∠3与∠4互补,并且∠1=∠3,那么∠2与∠4相等吗?为什么?
余角与补角的性质:
即,如果两个角相等,那么它们的余角(或补角)也 。
简称:等角的余角 ;等角的补角
如图,点O 在直线AB上,∠AOC=53°17′,
求∠BOC的度数?
练习1填表
已知一个角的补角是这个角的余角的3倍,求这个角的度数?
练习2:
1.一个角为(n<90°),则它的余角为 ,补角为 ;
2.如果,则的关系是 ,理由是 ;
3.一个角等于它的补角的5倍,则这个角的补角的余角是( )
A.30° B.60° C.45° D.50°
4. 如果与互补,与互余,则与的关系是( )
A.= B. C. D.以上都不对
5.和互补,且求和的度数。
6.一个角的余角比它的补角的还少,求这个角的度数。
角的比较与运算(3)
学习目标:
1、理解方位角的意义,掌握方位角的判别与应用.
2、通过现实情境,充分利用学生的生活经验去体会方位角的意义.
学习过程:
复习:已知一个角的补角是这个角的余角的3倍,求这个角。
探究新知
海上,缉私艇发现离它500海里处停着一艘可疑船只
(如图),立即赶往检查.现请你确定缉私艇的航向,
画出示意图.缉私艇舰长如何向总部描述缉私艇的航向呢?
在航行、测绘等工作以及生活中,我们经常会碰到上述类似问题,即如何描述一个物体的运动方向.
用 表示方向:一般以正北、正南为基准,用向东或向西旋转的 表示方向,
表示方向的角叫做
方位角通常用“北偏东多少度”、“北偏西多少度”或者“南偏东多少度”、“南偏西多少度”来表示.“北偏东45度”、“北偏西45度"、“南偏东45度”、“南偏西45度”,分别称为“东北方向”、“西北方向”,“东南方向”、“西南方向”。
例1 如图所示,
⑴说出射线OA,OB,OC分别表示的方向;
⑵在图中画出南偏东60°
说明:用量角器画表示方位的射线要注意两点:①是先从正南或正北方向作角的始边,②要分清东南西北,理解偏东、偏西的意义。
例2 一只小虫从点A出发向北偏西30°方向,爬行了3cm到点B,再从点B出发向北偏东60°爬了3cm到点C。
(1)试画图确定A、B、C的位置;(2)从图上量出点C到点A的距离(精确到0.1cm);
(3)指出点C在点A的什么方位
巩固练习
1.如图,点A位于点O的 方向上.( ).
A.南偏东35° B .北偏西65°
C .南偏东65° D .南偏西65°
2.已知点O在点A的南偏东30°方向,那么,点A应在点O的( )
A.南偏东30°方向; B.北偏东30°方向; C.北偏西30°方向; D.北偏西60°方向.
3.在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( )
A.100° B.70° C.180° D.140°
4.如图,由B到A的方向是( )
A.南偏东30° B.南偏东60°
C.北偏西30 D.北偏西60°
5.电视塔在学校的东北方向,那么学校在电视塔的 方向.
6.灯塔A在灯塔B的南偏西60°,A、B两灯塔相距20海里,现有一艘轮船C在灯塔B的正北方向、灯塔A的北偏东30°方向。试画图确定轮船的位置(每10海里用1厘米长的线段)
(A)
(B)
(C)
(D)
( 2)
( 1)
正面
左面
上面
D
C
B
A
⑵
⑴
A.
B.
C.
D.
正面
A.
B.
C.
D.
A. B. C. D.
A
B
C
D
3
4
2
1
5
6
第2题图
3
4
2
1
5
6
第3题图
第2题
建
设
和
谐
凉
山
迎
接
奥
运
圣
火
图1
迎
接
奥
1
2
3
图2
第一类:中间 个正方形
第二类:中间 个正方形
第三类:其他
①
·O
·A
·B
B BB
A
直线AB
·
·
a
直线a
O
b
a
点在直线外
·
B BB
·
点在直线上
A
·
a
·
B BB
A
O
A
m
·
②
①
a
a
b
A(C)
B
(D)
A(C)
(D)
B
A(C)
B(D)
A
B
M
A
B
M
N
(1)
(2)
()
A
B
E
C
B
A
F
E
C
B
A
F
D
C
B
O
A
O
B
C
A
E
F
O
C
B
A
D
C
B
A
O
缉私艇
可疑船
30°
C
B
A
东
西
南
北
O
80°
45°
A
650
O
一、学习目标
1.通过观察生活中的大量图片或实物,体验、感受、认识以生活中的事物为原型的几何图形;
2.认识一些简单几何体(长方体、正方体、棱柱、棱锥、圆柱、圆锥、球等)的基本特性;
3.能识别这些几何体.
二、学习过程
(一)自主学习:阅读课文P116-118,完成下列问题:
⑴ 对于生活中各种各样的物体,数学(几何学)关注的是它们的 、 、 。
⑵ 常见的立体图形有:
⑶ 常见的平面图形有: 。
⑷ 立体图形与平面图形的区别:
尝试应用
1.如下图所示,这些物体所对应的立体图形分别是: .
2.下列几种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;.其中属于立体图形的是( )
A. ①②③; B. ③④⑤; C. ③⑤; D.④⑤
3.图中的一些物体与我们学过的哪些图形相类似?把相应的物体和图形连接起来
例 看一看、想一想:说说圆柱、棱柱、圆锥、棱锥的异同
1、下列立方体图形有9个面的是 ( )
A、六棱锥 B、八棱锥 C、六棱柱 D、八棱柱
2.如图,左面的几何体叫三棱柱,它有五个面,9条棱,6个顶点,中间和右边的几何体分别是四棱柱和五棱柱。
(1)四棱柱有 个顶点, 条棱, 个面;
(2)五棱柱有 个顶点, 条棱, 个面;
(3)你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
(4)那么n棱柱呢?
几何图形(2)----立体图形的三视图
一、学习目标
1.经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果,了解为什么要从不同方向看.
2.能画出从不同方向看一些基本几何体(直棱柱、圆柱、圆锥、球)以及它们的简单组合得到的平面图形
二、学习过程:
苏东坡《题西林壁》:横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中。从数学的角度看:这首诗中蕴含何数学道理?
从不同方位看立体图形得到的图形一般是 的.
探究一:要设计如图示的一个工件,你认为设计师要画出
哪几张平面图形来表示它?请你画出来。
一般地:我们把从正面看到的图形叫 ,从左面看到的图形叫 ,从上面看到的图形叫 ,
画一画:长方体、圆锥分别从正面、左面、上面观察,各能得到什么图形?试着画一画.
练习1. 如图(1)放置的一个机器零件,若从正面看是如图(2),则其左面看是( )
2. 若右图是某几何体的三种不同方向的图,则这个几何体是( )
A.圆柱 B.正方体 C.球 D.圆锥
3. 图所示的物体,从左面看得到的图是( )
探究二:分别从正面、左面、上面观察这个图形,画出得到的平面图形
练习1. 如图所示是由四个相同的小正方体组成的立体
图形,它的俯视图为( )
2. 如图所示,一个斜插吸管的盒装饮料从正面看的图形是( )
3. 如图2,这是一个正三棱柱,则从上面看到的图为( )
4. 如图是由七个相同的小正方体堆成的物体,从上面看这个物体的图是( )
几何图形(3)----立体图形的平面展开图
一、学习目标
1.能直观认识立体图形和展开图,了解研究立体图形方法。
2.通过观察和动手操作,经历和体验平面图形和立体图形相互转换的过程,培养动手操作能力,初步建立空间观念,发展几何直觉。
二、学习过程:
问题:生活中,很多商品的包装盒都是长方体、圆柱体、圆锥等等,如何制作这些形状的纸制包装盒呢?
回顾复习:
1.画出圆柱、圆锥、长方体的表面展开图
探究一:画出 三棱柱、四棱锥的表面展开图
练习1.下面形状的四张纸板,按图中线经过折叠可以围成一下直三棱柱的是( )
2.如图,为一个多面体的表面展开图,每个面内都标注了数字.若数字为的面是底面,则朝上一面所标注的数字为( )
A.5 B.4
C.3 D.2
3. 如图,为一个多面体的表面展开图,每个面内都标注了数字.若数字为的面是左面,数字为5的面是前面,则朝上一面所标注的数字为( )
A.5 B.4 C.3 D.2
探究二:画出正方体的各种表面展开图,你能画几种呢?
练习1.下列图形中,不是正方形的表面展开图的是( )
A. B. C. D.
2. 如图是一个正方体的表面展开图,则图中“加”字所在面的对面所标的字是( )
A.北 B.京 C.奥 D.运
3. 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐
C.凉 D.山
4. 如图(1)是一个小正方体的侧面展开图,小正
方体从图(2)所示的位置依次翻到第1格、第2格、
第3格,这时小正方体朝上一面的字是( )
A.奥 B.运 C.圣 D.火
正方体的各种表面展开图
点、线、面、体
一、学习目标
(1)了解几何体、平面和曲面的意义,能正确判定围成几何体的面是平面还是曲面; ( http: / / )
(2)了解几何图形构成的基本元素是点、线、面、体及其关系,能正确判定由点、线、面、体经过运动变化形成的简单的几何图形.
二、学习过程:
复习:如右图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 块小正方体;
(2)请在下面分别画出它的主视图、左视图和俯视图.
问题:
常见的立体图形有哪些?说出下列几何体的名称: 。
立体图形又叫几何体简称 。
探究:
⑴ 观察长方体和圆柱体,说出围成这两个几何体的面有哪些?这些面有什么区别?
包围着体的是 ,面有 面和 面两种。
⑵长方体有几个面?面和面相交成了几条线?线和线相交成几个点?
面和面相交成 , 线有 线和 线两种。线和线相交成 。
练习1:围成下面这些立体图形的各个面中,哪些面是平的?哪些面是曲的?
2 “当你远远地去观察霓虹灯组成的图案时,图案中的每个霓虹灯就是一个点;在交通图上,点用来表示每个地方;电视屏幕上的画面也是由一个个小点组成;运用点可以组成数字和字母,这正是点阵式打印机的原理.”说说你对上述这段叙述的理解和体会.
几何图形都是由 、 、 、 组成; 是组成几何图形的基本元素。
探究:⑴ 粉笔头可以看做一个 ,粉笔头在黑板上移动就形成一条 ;
⑵ 一条线段绕其端点旋转一周,形成一个 ;
⑶ 一个直角三角板绕其直角边旋转一周,形成一个 。
由此得到:点动成 ,线动成 ,面动成 。
请你举出生活中更多的“点动成线、线动成面、面动成体”的例子。
练习1.灿烂的星空,有流星划过天际形成一条 ,这说明了 的数学原理.
2.体是由 围成的,面和面相交于 ,线和线相交于 .
3.点动成 ,线动成 ,面动成 .
4.把下面第一行的平面图形绕线旋转一周,便能形成第二行的某个几何体,请用虚线连一连:
5.将下面五个图形折叠,你能说出这些多面体的名称吗
6.从三个方向看一个立方体(如图),则A、B、E对面分别是字母________
直线、射线、线段(1)
学习目标
1、认识直线、射线、线段及它们的联系和区别,掌握它们的表示方法;2、了解“两点确定一条直线”的性质;3、能根据语句画出相应的图形,会用语句描述简单的图形。
学习过程]
一、导入新课
我们知道,点是几何研究的最基本的图形,点动成线,线有直线、射线和线段。今天我们就来学习这些简单的几何图形。
二、直线及其性质
探究:
如图①,要在墙上固定一根木条,
使它不能转动,至少需要几颗钉子?
(2)如下图,经过一点O画直线,能画出几条?经过点A、点B两点呢?
由此可得一个基本事实:
经过两点有 条直线,而且只有 条直线。简述为:两点确定一条直线。
你能再举几个这样的例子吗?
直线有两种表示方法:①用一个小写字母表示;②用两个大写字母表示。
平面上一个点与一条直线的位置有什么关系?
①点在直线上;②点在直线外。
一个点在一条直线上,也可以说这条直线经过这个点如图①,一个点不在一条直线上,也可以说这条直线不经过这个点,如图②。
当两条直线有一个共公点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
三、射线和线段
我们手中的直尺给我们线段的形象,手电筒发出的光给我们射线的形象,如图。显然,射线和线段都是直线的一部分。
图①中的线段记作线段AB或线段a;图②中的射线记作射线OA或射线m。
注意:用两个大写字母表示射线时,表示端点的字母一定要写在前面。
思考:直线、射线和线段有什么联系和区别?
性质与表法名称 端点 个数 能否度量 向几方延伸 图形 称呼与表示
直 线
射 线
线 段
四、应用新知
例 读下列语句,并按照语句画出图形:
(1)画线段AB(也叫连接AB);⑵直线经过A、B两点,点B在点A的左边;⑶直线AB、CD都经过点O,点E不在直线AB上,但在直线CD上。
解:
练习:1、植树时,要确定一行树的位置,只需确定这一行树中任两棵树的位置,其中体现的数学道理是______________________.
2、将线段一端延伸能得到______,将线段两端都延伸能得到______.
3、图中共有几条线段?几条射线?几条直线?能用字母表示出来的分别用字母表示出来。
4、如图,点C在直线AB______. 点O在直线BD______. O点是_______的交点. 过点A的直线共有_____条,它们是_________.
5、按下列语言作图
(1)连接AB、CD
(2)作直线AD
(3)作射线CB,交直线AD于点O
(4)过点O作一条直线,交线段AB
于点M,交线段CD于N.
直线、射线、线段(2)
学习目标:
1、会用尺规画一条线段等于已知线段;2、会比较两条线段的长短;3、理解线段中点的概念,了解“两点之间,线段最短”的性质。
学习过程:
一、问题导入
现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长?
上面的实际问题可以转化为下面的数学问题:
已知线段a,画一条线段等于已知线段a。
二、作一条线段等于已知线段
现在我们来解决这个问题。
作法:(1)
(2)
例1 已知线段a、b,求作线段AB=a+b
解:
做一做:作线段AB=a-b。
三、比较两条线段的长短
两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢?我们先来回答下面的问题。
怎样比较两个同学的身高?
一是: ;二是: 。
如果把两个同学看成两条线段,那么比较两条线段就有两种方法。
1、度量法:用刻度尺分别量出两条线段的长度从而进行比较。
2、叠合法:把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。
记作: AB CD AB CD AB CD
四、线段的中点及等分点
如图(1),点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点。
记作:AM=MB或AM=MB=AB或2AM=2MB=AB。
如图(2),点M、N把线段AB分成相等的三段AM、MN、NB,点M、N叫做线段AB的 等分点。类似地,还有四等分点,等等。
五、线段的性质
如图,从A地到B地有三条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线。
这说明了什么呢?
两点所连的线中,线段 。简单地说成:
两点之间,线段 。
连接两点间的线段的长度叫做这两点间的距离。
注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。
六、巩固练习
1.线段AB=8cm,C是AB的中点,D是BC的中点,A、D两点间的距离是_____cm.
2.如图3,在直线I上顺次取A、B、C、D四点,则AC=______+BC=AD-_____,AC+BD- BC=________.
3.下列语句准确规范的是( )
A. 直线a、b相交于一点m B. 延长直线AB
C. 反向延长射线AO(O是端点) D. 延长线段AB到C,使BC=AB
4.如果点C在AB上,下列表达式①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
5. 已知点C是线段AB的中点,点D是线段BC的中点,CD=2.5厘米,请你求出线段AB、AC、AD、BD的长各为多少?
6. 如图,DB=3cm,BC=7cm,C是AD的中点,求AB的长.
7.画线段AB=10mm,延长AB至C,使BC=15mm,再反向延长线段AB至D,使DA=15mm,先依题意画出图形,并求出DC的长
直线、射线、线段(3)
学习目标:
1、利用直线、线段的性质解决相关实际问题;
2、利用线段的中点定义解决相关计算问题.
学习过程:
复习:⑴某村庄和小学分别位于两条交叉的大路边,可是有些人不爱惜庄稼,
每年冬天麦田里总会走出一条小路来,其中的数学道理是________________________.
⑵读出下列语句,并按照语句画出图形.
① 点C在直线AB上,而点D在直线AB外; ② 直线AB和直线BC相交于B;
③ 经过点A的四条直线a,b,c,d; ④ 延长线段AB到C,使AC=3AB .
例1 已知线段AB=10㎝, C是线段AB上任意一点,E、F分别是AC、BC的中点,求线段EF的长?
练习1:⑴已知线段AB及一点P,若AP+PB=AB,则点P在
⑵. 已知C是线段AB上的一点,D是CB的中点,DB=2cm,AC=8cm,则AB=__ cm.
⑶ 如图,C、D是线段AB上的两点,且AC=CB,CD=DB,则线段AB的中点是点___,点D 是线段____的中点,AC=__DB,DB=__AB.
⑷ 已知线段AB=10, 点C在直线AB上,且AC=4,若点D是AB的中点,求DC的长.
例2 已知C、D是线段AB上的两点,且AC︰CD︰DB=2︰3︰4,E、F分别是AC、DB的中点,如果EF=12㎝,求线段AB的长?
【巩固练习】
⑴ 在同一个学校上学的小明、小伟、小红三位同学住在A、B、C三个住宅区,如图2所示,A、B、C三点共线,且AB=60米,BC=100米,他们打算合租一辆接送车去上学,由于车位紧张,准备在此之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在何处?
⑵线段AB=4cm,延长线段AB到C,使BC = 1cm,再反向延长AB到D,使AD=3 cm,E是AD中点,F是CD的中点,求EF的长度。
⑶ 将线段AB延长至C,使BC=AB,延长BC至点D,使CD=BC,延长CD至点E,使DE=CD,若CE=8㎝,求AB的长?
角(1)
学习目标:
1、通过丰富的实例,理解角的形成,建立几何中角的概念,掌握角的两种定义形式和四种表示方法.
2、通过在图片、实例中找角,培养学生的观察、探究、抽象、概括的能力以及把实际问题转化为数学问题的能力。
学习过程:
一、提出问题(前几节课我们一起研究和讨论了线段,射线,直线的特点和性质,今天就来研究另一种图形——角)
⑴请你根据小学对角的认识与理解,画一个角。
⑵角的两边是 ;他们的位置关系如何?根据自己的理解试给角下一个定义?
探究:
(一)角的概念
角的定义:有 组成的图形叫做角.这个公共端点是角的 ,这两条射线是角的 .
举出几个生活中给我们角的形象的物体: 。
(二)角的表示方法:
在刚才的讨论中,我们发现了生活中有许多角的形象.那么,我们如何给这些角取名呢?
①用三个大写字母表示:∠AOB(顶点写在中间)
②用一个大写字母表示:∠O(用顶点表示,该顶点处只有一个角)
③用一个希腊字母表示:∠α(用小弧圈在图中表示)
④用数字表示:∠1(用小弧圈在图中表示)
例1 如图,回答下列问题。(1)写出图中能用一个字母表示的角;(2)写出以B为顶点的角;(3)图中共有几个角 分别把它们表示出来。
练习
1.如下左图所示,把图中用数子表示的角,改用大写字母表示分别是________ .
( http: / / www. / )
2.将上右图中的角用不同的方法表示出来,填入下表:
∠1 ∠3 ∠4
∠BCA ∠ABC
(三)用旋转观点定义角
角也可以看成是由一条射线绕着它的端点旋转而形成的图形.
当射线OA绕点O旋转时,当终止位置OB和起始位置OA成一条直线时,会形成什么角?继续旋转,当OB和OA重合时,又形成什么角?
① 绕着端点旋转到角的终边和始边成一直线,这时所成的角叫做 ;
② 绕着端点旋转到角的终边和始边再次重合,这时所成的角叫做 。
③ 小于180°角可以分成: 、 、 。
应用
1.把图中的角表示成下列形式,哪些正确,哪些不正确?
(1)∠APO (2)∠AOP (3)OPC (4)∠OCP
(5)∠O (6) ∠P
2.图中以O点为顶点的角有几个?以D点为顶点的角有几个?试用适当的方法来表示这些角。
巩固练习
1.下列说法错误的是( )
A.平角的一半是直角 B.平角的两倍是周角 C.锐角的两倍是钝角D.钝角的一半是锐角
2.下列说法正确的是
A. 角的两条边在同一条直线上的角是周角 B.五角星图形中有五个角
C. 18时整,时针和分针成一个平角 D.长方体表面上只有四个角
3.画射线OA,OB;在∠AOB的内部和外部分别画射线OC, OD.那么所画的图中有哪几个角?请用适当的方法表示这些角.
角的度量(2)
学习目标:
1、认识度、分、秒,会进行度、分、秒间单位互化及角的和、差、倍、分计算.
2、通过度、分、秒间的互化及角度的简单运算,经历利用已有知识解决新问题的探索过程.
学习过程:
复习回顾
任意画一个锐角和钝角,用字母分别表示这两个角,用量角器分别量出这两个角的度数。
探究新知:
角度制(阅读课文P137内容,完成下列填空)
我们常用量角器量角.在量角器中看到,把一个平角 等分,每一份就是 的角.记作1°
在实际生活中,有时还需要更精密的角度.因此我们把1度的角 等分,每份就是 的角,记作;把1分的角 等分,每份就是 的角,记作1".
角的度量:
1周角= 1平角= 1直角=
1°= 1′= 1°= ″
归纳:以度、分、秒为单位的角的度量制叫做 .
想一想:角度进位制和其他什么进位制相类似?
2、回顾两个问题:
问题① 3.32小时= 小时 分 秒; 问题② 12小时9分36秒= 小时;
例1 ⑴ 用度、分、秒表示48.12°;⑵ 用度表示50°7′30″;⑶= 度
例2 计算: ⑴ +; ⑵ ; ⑶ ×4
例3 把一个周角7等分,每一份是多少度的角?(精确到分)
练习
1.()°=_____′=_____″; 6000″=______′=_______°.
2.在钟表上,1点30分时,时针与分针所成的角是( ).
A.150° B.165° C.135° D.120°
3.下列各角中,不可能是钝角的角是( ).
A.周角 B.平角 C.钝角 D.直角
4.计算
(1)53°28′+47°32′; (2)17°50′-3°27′;
⑶ 48°39′+67°41′ ⑷ 90°-78°19′40″;
⑸ 15°24′×5; ⑹31°42′÷5(精确到1″).
角的比较与运算(1)
学习目标:
1、会比较角的大小,能估计一个角的大小.在操作活动中认识角的平分线;
2、实际观察、操作,体会角的大小,培养学生的观察思维能力;
学习过程:
复习回顾
如图(1),已知线段AB和线段CD,如何比较这两条线段的大小呢?
探究新知:
问题1:如图(2)已知∠ABC和∠DEF。请大家讨论一下,用什么方法可以比较这两个角的大小?
1、角的大小的比较方法:
;
。
2、角的和差.
观察下列图形,图中共有几个角?图中各角之间有怎样的和差关系?
① ∠AOB+∠BOC= ;② ∠AOC-∠AOB=
③∠AOC-∠AOB=________.
练习1:一副三角板,各角的度数分别是多少度?你能用一副三角板画出哪些度数的角?
问题2:在一张纸上画出一个角并剪下,将这个角对折,使其两边重合.想想看,折痕与角两边所成的两个角的大小有什么关系?
3.角的平分线
从一个角的顶点出发,把这个角分成 的两个角的射线,叫做这个角的平分线。类似的还有角的三等分线、四等分线等等.
⑴如果OC平分∠AOB,你能得到哪些结论?
⑵想一想,有什么方法可画出一个角的平分线呢?
画一画:按下列语句画图:
① 画一个∠AOB;② 在∠AOB的两边上分别取OC=OD=4cm;③ 连结CD;④ 作出CD的中点E;⑤ 画射线OE. 猜想OE与∠AOB的关系?
例1 如图,已知∠AOC=120°如果OB是∠AOC内任意射线,OE,OF分别是∠AOB,∠BOC的平分线.求:∠EOF的度数.
巩固练习
1.如果∠1=∠2,∠1+∠3=90°,则∠2+∠3=_______.
2.如图,有“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB-∠BOC; (2)∠AOC_______∠AOB;
(3)∠BOD-∠BOC______∠DOC; (4)∠AOB______∠AOC+∠BOD.
3.如图,OC平分∠AOB,OD平分∠AOC,
①图中相等的角有_______ ;
②∠AOD=______∠AOC=______∠AOB.
4.如下图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,
求∠AOB的度数.
角的比较与运算(2)
学习目标:
1、在具体情境中了解余角与补角.懂得等角的余角相等,等角的补角相等.并能运用这些性质解决一些简单的实际问题;
2、经历观察、操作、推理、交流等活动,发展学生的空间观念,培养学生的推理能力和有条理的表达能力;
学习过程:
复习:说出一副三角尺中各个角的度数:① 、② 。
探究新知:
余角与补角的概念(预习课文P141,完成下列填空)
⑴ 如果两个角的和等于 ( ),我们就说这两个角 ,简称互余。即其中一个角是另一个角的 .
例如:如果∠1+∠2=90°,那么∠1与∠2 ,∠1是 的余角,∠2也是∠1的
⑵ 如果两个角的和等于 度 ( ),就说这两个角 ,简称互补。即其中一个角是另一个角的 .
例如:如果∠1与∠2互补,那么∠1+∠2= ,
2、余角与补角的性质
问题1:如果∠1与∠2互余,∠3与∠4互余,并且∠1=∠3,那么∠2与∠4相等吗?为什么?
问题2:如果∠1与∠2互补,∠3与∠4互补,并且∠1=∠3,那么∠2与∠4相等吗?为什么?
余角与补角的性质:
即,如果两个角相等,那么它们的余角(或补角)也 。
简称:等角的余角 ;等角的补角
如图,点O 在直线AB上,∠AOC=53°17′,
求∠BOC的度数?
练习1填表
已知一个角的补角是这个角的余角的3倍,求这个角的度数?
练习2:
1.一个角为(n<90°),则它的余角为 ,补角为 ;
2.如果,则的关系是 ,理由是 ;
3.一个角等于它的补角的5倍,则这个角的补角的余角是( )
A.30° B.60° C.45° D.50°
4. 如果与互补,与互余,则与的关系是( )
A.= B. C. D.以上都不对
5.和互补,且求和的度数。
6.一个角的余角比它的补角的还少,求这个角的度数。
角的比较与运算(3)
学习目标:
1、理解方位角的意义,掌握方位角的判别与应用.
2、通过现实情境,充分利用学生的生活经验去体会方位角的意义.
学习过程:
复习:已知一个角的补角是这个角的余角的3倍,求这个角。
探究新知
海上,缉私艇发现离它500海里处停着一艘可疑船只
(如图),立即赶往检查.现请你确定缉私艇的航向,
画出示意图.缉私艇舰长如何向总部描述缉私艇的航向呢?
在航行、测绘等工作以及生活中,我们经常会碰到上述类似问题,即如何描述一个物体的运动方向.
用 表示方向:一般以正北、正南为基准,用向东或向西旋转的 表示方向,
表示方向的角叫做
方位角通常用“北偏东多少度”、“北偏西多少度”或者“南偏东多少度”、“南偏西多少度”来表示.“北偏东45度”、“北偏西45度"、“南偏东45度”、“南偏西45度”,分别称为“东北方向”、“西北方向”,“东南方向”、“西南方向”。
例1 如图所示,
⑴说出射线OA,OB,OC分别表示的方向;
⑵在图中画出南偏东60°
说明:用量角器画表示方位的射线要注意两点:①是先从正南或正北方向作角的始边,②要分清东南西北,理解偏东、偏西的意义。
例2 一只小虫从点A出发向北偏西30°方向,爬行了3cm到点B,再从点B出发向北偏东60°爬了3cm到点C。
(1)试画图确定A、B、C的位置;(2)从图上量出点C到点A的距离(精确到0.1cm);
(3)指出点C在点A的什么方位
巩固练习
1.如图,点A位于点O的 方向上.( ).
A.南偏东35° B .北偏西65°
C .南偏东65° D .南偏西65°
2.已知点O在点A的南偏东30°方向,那么,点A应在点O的( )
A.南偏东30°方向; B.北偏东30°方向; C.北偏西30°方向; D.北偏西60°方向.
3.在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( )
A.100° B.70° C.180° D.140°
4.如图,由B到A的方向是( )
A.南偏东30° B.南偏东60°
C.北偏西30 D.北偏西60°
5.电视塔在学校的东北方向,那么学校在电视塔的 方向.
6.灯塔A在灯塔B的南偏西60°,A、B两灯塔相距20海里,现有一艘轮船C在灯塔B的正北方向、灯塔A的北偏东30°方向。试画图确定轮船的位置(每10海里用1厘米长的线段)
(A)
(B)
(C)
(D)
( 2)
( 1)
正面
左面
上面
D
C
B
A
⑵
⑴
A.
B.
C.
D.
正面
A.
B.
C.
D.
A. B. C. D.
A
B
C
D
3
4
2
1
5
6
第2题图
3
4
2
1
5
6
第3题图
第2题
建
设
和
谐
凉
山
迎
接
奥
运
圣
火
图1
迎
接
奥
1
2
3
图2
第一类:中间 个正方形
第二类:中间 个正方形
第三类:其他
①
·O
·A
·B
B BB
A
直线AB
·
·
a
直线a
O
b
a
点在直线外
·
B BB
·
点在直线上
A
·
a
·
B BB
A
O
A
m
·
②
①
a
a
b
A(C)
B
(D)
A(C)
(D)
B
A(C)
B(D)
A
B
M
A
B
M
N
(1)
(2)
()
A
B
E
C
B
A
F
E
C
B
A
F
D
C
B
O
A
O
B
C
A
E
F
O
C
B
A
D
C
B
A
O
缉私艇
可疑船
30°
C
B
A
东
西
南
北
O
80°
45°
A
650
O
