六年级下册数学习题课件-4 比例 人教版(共62张PPT)
文档属性
| 名称 | 六年级下册数学习题课件-4 比例 人教版(共62张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 09:46:57 | ||
图片预览










文档简介
(共62张PPT)
4
比
例
第1课时 比例的意义
1.
填空。
(1)
表示(
)相等的(
)叫做比例。
(2)
12∶9的比值是(
),∶的比值是(
),把这两个比写成比例是
(
)。
(3)
写出比值是0.5的两个比是(
)和(
),它们组成的比例是
(
)。
(4)
24的因数有(
),从中选出4个不同的数组成比例
是(
)。
两个比
式子
12∶9=∶
1∶2
2∶4
1∶2=2∶4
(答案不唯一)
1,2,3,4,6,8,12,24
1∶2=3∶6
(最后一空答案不唯一)
2.
选择。
(1)
下面各组比中,能组成比例的是(
)。
①
10∶12
和
24∶36
②
16∶4
和
8∶2
③
∶
和
18∶12
(2)
下面能与∶组成比例的是(
)。
①
6∶8
②
1∶6
③
4∶3
3.
把能组成比例的两个比用线连起来。
7∶14
∶0.8 7.5∶5
7∶12
?
30∶48
∶
∶
8.4∶16.8
②
③
4.
小明买同一种练习本,第一次用4.8元买了6本,第二次用8元买了10本。
(1)
第一次与第二次所用钱数的比是(
),比值是( )。第一次与
第二次所买本数的比是(
),比值是( )。这两个比能组成比例吗?
为什么?
(2)
第一次所用的钱数与买的本数的比是(
),比值是(
)。第
二次所用的钱数与买的本数的比是(
),比值是(
)。这两个比
能组成比例吗?为什么?把组成的比例写出来。
4.8∶8
6∶10
能组成比例 因为它们的比值相等
4.8∶6
0.8
8∶10
0.8
能组成比例 因为它们的比值相等 4.8∶6=8∶10
5.
下面各表中相对应两个量的比能否组成比例?如果能,把组成的比例写出来。
(写出1组)
(1)
(2)
零件总数/个
480
720
时间/时
4
6
已看页数
25
86
未看页数
175
114
能组成比例 答案不唯一,
如480∶4=720∶6
不能组成比例
6.
下面各组中的数可以组成比例吗?如果可以,把组成的比例写出来。(写出1组)
(1)
4,20,5和1
(2)
0.9,12,3.6和0.3
?
?
(3)
,,30和24
(4)
0.5,0.4,和
可以组成比例,答案不唯一,如4∶20=1∶5
不能组成比例
可以组成比例,答案不唯一,如30∶
=24∶
可以组成比例,答案不唯一,
如0.5∶0.4=
∶
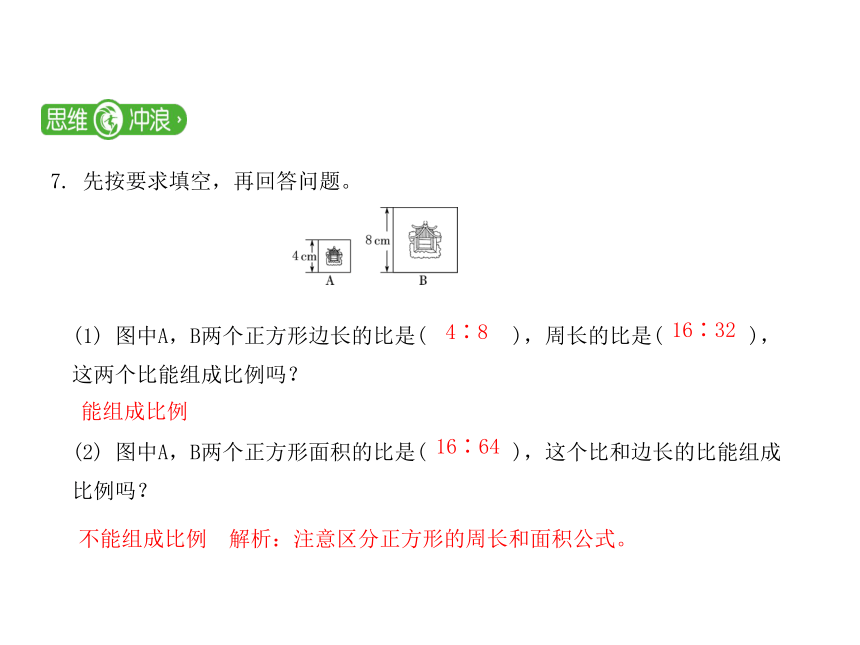
7.
先按要求填空,再回答问题。
(1)
图中A,B两个正方形边长的比是(
),周长的比是(
),
这两个比能组成比例吗?
(2)
图中A,B两个正方形面积的比是(
),这个比和边长的比能组成
比例吗?
能组成比例
不能组成比例 解析:注意区分正方形的周长和面积公式。
4∶8
16∶32
16∶64
第2课时
比例的基本性质
1.
填空。
(1)
如果7a=11b(a,b都不为0),那么a∶b=(
)∶(
)。
(2)
在比例中,两个(
)的积等于两个(
)的积,这叫做(
)。
(3)
在比例2∶0.5=1.2∶0.3中,外项是(
)和(
);在比例=中,两
个内项分别是(
)和(
)。
(4)
如果=,那么x×(
)=y×(
)。
(5)
在一个比例中,两个外项互为倒数,若其中一个内项是,则另一个内项是
(
)。
11
7
外项
内项
比例的基本性质
2
0.3
1.2
35
5
4
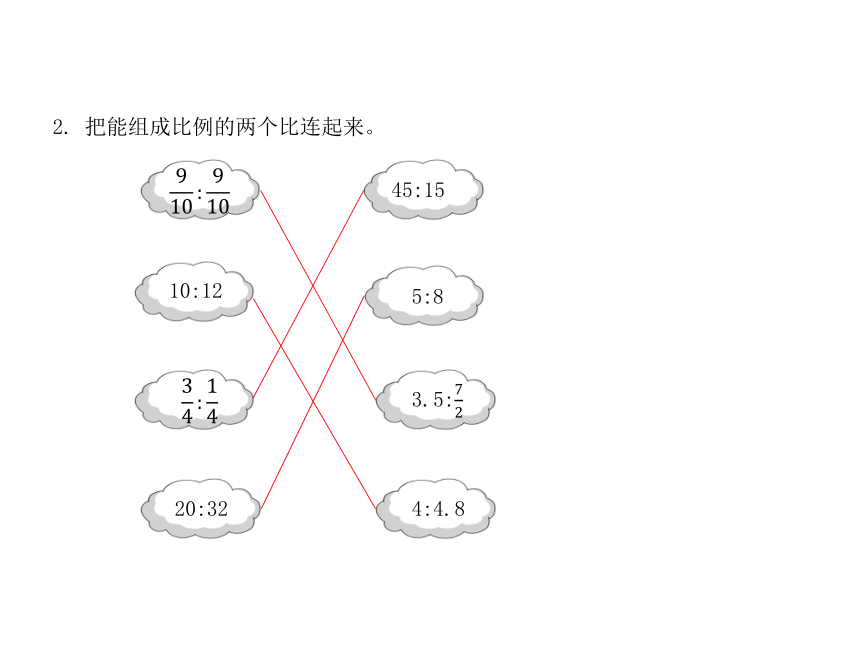
2.
把能组成比例的两个比连起来。
45:15
10:12
5:8
3.5:
20:32
4:4.8
3.
根据比例的基本性质,在( )里填上合适的数。
(1)
24∶4=(
)∶1
(2)
3∶0.5=1.2∶(
)
(3)
=
(4)
∶(
)=∶
4.
判断。
(1)
在一个比例中,两个外项的积与两个内项的积的差是0。(?
)
(2)
如果0.5∶9=m∶n,那么0.5m=9n。(
?)
(3)
5∶35=1∶7,还可以写成=。(?
)
(4)
在一个比例中,两个内项分别是4和5,两个外项的积一定是20。(
?)
(5)
如果5a=4b(a,b都不为0),那么b∶a=4∶5。(?
)
6
0.2
0.9
√
×
√
√
×
5.
已知3×40=5×24,根据比例的基本性质,把这个等式改写成比例,你能写几
个?把组成的比例写出来。
6.
把8,40,32再配一个数分别满足下面的条件组成比例。
(1)
把8和40同时作为外项(或内项),再配上(
)可以组成比例。
(2)
把8和32同时作为外项(或内项),再配上(
)可以组成比例。
(3)
把40和32同时作为外项(或内项),再配上(
)可以组成比例。
4个 3∶5=24∶40 3∶24=5∶40 5∶3=40∶24 24∶3=40∶5
10
6.4
160
7.
两个比的比值都是6,它们组成的比例的内项都是1.2,写出这个比例。
7.2∶1.2=1.2∶0.2
解析:解题的关键点要理解“它们组成的比例的内项都是1.2”,然后根据“两个比的比值是6”,求第一个比的前项和第二个比的后项。
第3课时
解
比
例
1.
填空。
(1)
解比例的依据是(
)。
(2)
在( )里填上合适的数。
3∶7=5∶(
)
20∶(
)=4∶9
8∶=(
)∶0.5
3.5∶1.4=8.2∶(
)
(3)
将4,5,6再配上一个数组成比例,那么这个数可以是(
)或(
)或(
)。
(4)
如果两个外项的积是最小的合数,其中一个内项是,那么另一个内项是
(
)。
(5)
一项工程,甲单独做10天完成,乙单独做12天完成,甲、乙两人工作效率的
比是(
)∶(
)。
比例的基本性质
45
6
3.28
4.8
7.5
16
6
5
2.
解下面的比例。
x∶45=8∶12
∶=∶x
=
=8∶x
3.
根据下面的条件列出比例,并解比例。
(1)
在一个比例里,两个内项分别是x和0.6,两个外项分别是5.1和1.7。
(2)
0.4与x的比等于3与的比。
(3)
最小的质数与最大的一位数的比等于与x的比。
x=30
x=
x=5
x=36
5.1∶x=0.6∶1.7 x=14.45(列比例不唯一)
0.4∶x=3∶ x=
2∶9=∶x x=
4.
某地上午10时,电线杆的高度与其在地上的影子的长度之比是4∶3。已知影子
的长度是6
m,求电线杆的高度。
5.
有大、小两个圆,大圆的直径是12
cm,大圆的周长与小圆的周长的比是3∶2。
小圆的直径是多少厘米?
6.
某工程队修一条公路,已经修了1800
m,已修的长度与未修的长度的比是3∶5。
这条公路长多少米?
设电线杆的高度为x
m。 x∶6=4∶3 x=8
设小圆的直径为x
cm。 12∶x=3∶2 x=8
设这条公路长x
m。 1800∶x=3∶(5+3) x=4800
7.
音乐兴趣班有男生24人,女生18人,又转入部分女生后,男、女生人数的比是
6∶5。
设转入女生x人。 24∶(18+x)=6∶5 x=2
解析:本题要注意转入的是女生,男生人数不变。
第4课时
正
比
例
1.
填空。
(1)
两种相关联的量,一种量变化,另一种量也随着(
),如果这两种量中
(
)的两个数的(
)一定,这两种量就叫做成正比例的量。
(2)
如果用字母y和x表示两种相关联的量,用k表示它们的比值(
),正比例
关系可以用式子表示为(
)。
(3)
某班订阅《小学生周报》的数量和总价如下表。
①
表中相关联的两种量是(
)和(
),这两种量相对应的两个数的比值都
是(
),这个比值的意义是(
)。
②
因为比值一定,所以表中的两个量叫做成(
)的量。
数量/份
1
2
3
4
5
6
总价/元
1.5
3
4.5
6
7.5
9
变化
相对应
比值
一定
=k
总价
数量
1.5
《小学生周报》的单价
正比例
2.
某品牌雪糕的销售量和销售额的关系如下表。
(1)
写出几组销售额与相对应的销售量的比,并比较比值的大小。
(2)
这个比值表示什么?
(3)
该品牌雪糕的销售额与销售量成正比例关系吗?为什么?
(4)
在下图中描出表示该品牌雪糕的销售额与相对应的销售量的点,然后把这些
点按顺序连接起来。
销售量/箱
4
5
6
7
8
…
销售额/元
240
300
360
420
480
…
240∶4 300∶5 360∶6 420∶7 480∶8 比值相等,都是60
该品牌雪糕的单价
成正比例关系 因为它们的比值固定不变
略
3.
判断下面各题中的两种量是否成正比例关系,是的画“√”,不是的画“×”。
(1)
某种饮料的单价不变,购买饮料的数量与总价。(?
)
(2)
李想的身高与年龄。(?
)
(3)
圆的周长与它的直径。(?
)
(4)
一杯水,喝掉的与剩下的。(?
)
(5)
工作时间一定,工作总量与工作效率。(
?)
√
×
√
×
√
4.
把下表补充完整。
(1)
根据表中的数据,在下图中描出织布的数量和织布的时间所对应的点,再
把它们按顺序连接起来。
(2)
织布的数量与织布的时间成正比例吗?为什么?
(3)
根据图象推算,织布50米需要(
)小时,8小时织布(
)米。
织布的时间/时
1
2
3
5
…
织布的数量/米
20
40
60
80
…
略
成正比例关系 因为织布的数量与织布的时间之间的比值一定
2.5
160
4
100
6.
下表是关于正方体钢块的一些量,哪两种量成正比例关系?(每立方厘米钢块
的质量是一定的)
棱长/cm
1
2
3
4
5
6
底面积/cm2
1
4
9
16
25
36
表面积/cm2
6
24
54
96
150
216
体积/cm3
1
8
27
64
125
216
质量/g
7.8
62.4
210.6
499.2
975
1684.8
表面积与底面积 质量与体积 解析:要求哪两种量成正比例关系就是求这两种量中相对应的两个数的比值一定。
5.
已知y与x成正比例关系,试填写下表。
x
20
60
480
120
y
2.5
6
0.5
0.25
200
0.75
1.5
40
第5课时
反
比
例
1.
填空。
(1)
小明用一定的钱买一种饮料,单价与购买饮料的瓶数的情况如下表。
观察上表我们发现,饮料的瓶数随着(
)的变化而变化。单价增加,饮料的瓶
数(
);单价减少,饮料的瓶数(
)。而且(
)与(
)的
(
)一定,我们就说(
)与(
)成(
)比例关系。
(2)
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系
可以用式子表示为(
)。
(3)
当a+b=2.4时,a与b(
)比例关系;当a·b=2.4时,a与b(
)
比例关系。(填“成”或“不成”)
单价/元
1
2
3
4
数量/瓶
60
30
20
15
单价
减少
增加
单价
饮料的瓶数
乘积
单价
饮料的瓶数
反
xy=k
不成
成
2.
工厂加工一批零件,每小时加工的数量和工作时间如下表。
(1)
每小时加工的数量与工作时间有什么变化规律?
(2)
分别求出各组每小时加工的数量与相对应的工作时间的积,比较积的大小。
(3)
说明这个积所表示的意义。
(4)
每小时加工的数量与相对应的工作时间成反比例关系吗?为什么?
每小时加工的数量/个
10
20
30
40
50
60
工作时间/时
60
30
20
15
12
10
每小时加工的数量随着工作时间的减少而增加
10×60=20×30=30×20=40×15=50×12=60×10=600 积相等,都等于600
这个积表示这批零件的总数量是一定的,为600个
成反比例关系 因为它们的乘积一定
3.
判断下面各题中的两种量是否成反比例关系,是的画“√”,不是的画“×”。
(1)
比的前项一定,比的后项与比值。(
?)
(2)
成活率一定,栽树总棵数与成活棵数。(
?)
(3)
修一条路,工作效率与工作时间。(
?)
(4)
一个人的年龄与体重。(?
)
(5)
路程一定,速度与时间。(?
)
√
×
√
×
√
4.
已知x与y成反比例关系,填写下表。
x
24
6
2.5
…
y
5
15
16
…
5.
看图回答问题。
(1)
速度与时间是否成反比例关系?
(2)
当速度为80
km/h时,所用时间是多少?
速度与时间成反比例关系
10×10÷80=1.25(h)
20
8
48
7.5
6.
已知两种量A,B满足等式×7=×B,A与B成比例关系吗?如果成比例关系,
那么成什么比例关系?
成比例关系 A与B成反比例关系 解析:由×7=×B,可知=,即A×B=7×7=49(一定),所以A与B成比例关系且成反比例关系。
第6课时
练
习
课
1.
填空。
(1)
因为ab=3.2,所以a与b成(
)比例关系。
(2)
若=,则x与y成(
)比例关系。
(3)
因为=y(x,y均不为0),所以x与y成(
)比例关系。
(4)
因为3x=4y,所以x与y成(
)比例关系。
2.
选择。
(1)
圆的周长与(
)成正比例关系。
①
圆的面积
②
圆的直径
③
圆周率
(2)
用地砖铺一间教室,所需地砖的块数与(
)成反比例关系。
①
每块地砖的边长
②
每块地砖的面积
③
每块地砖的周长
反
正
反
正
②
②
(3)
若甲数与乙数互为倒数,则甲数与乙数(
)比例关系。
①
成正
②
成反
③
不成
(4)
下面四句话中,正确的是(
)。
①
三角形的面积一定,它的高与对应的底成正比例关系
②
车轮的周长一定,车轮行驶的路程和转数成反比例关系
③
圆的直径一定,周长和圆周率成正比例关系
④
花生的出油率一定,榨出花生油的质量与花生的质量成正比例关系
②
④
3.
已知表1和表2中x与y分别成正比例关系和反比例关系,请把表格补充完整。
表
1
y
160
130
0.5
x
8
1.5
0.4
表
2
x
3
6
24
y
16
48
8
30
6.5
8
0.025
64
12
32
4
4.
下面的图象表示的是购买甲、乙两种练习本的数量和总价的变化情况。
(1)
两种练习本各买5本,分别需要多少元?
(2)
从图上看,哪种练习本便宜些?
5.
如果=1(b≠0,c≠0),那么:
(1)
当a一定时,b和c成(
)比例关系。
(2)
当b一定时,a和c成(
)比例关系。
(3)
当c一定时,a和b成(
)比例关系。
买5本甲种练习本需要10元,买5本乙种练习本需要5元
乙种练习本便宜些
反
正
正
6.
一个平行四边形的面积是60
cm2,分别用x和y表示它的底和其对应的高,x与y
成什么比例关系?如果把它们的关系用图象表示出来,那么图象是一条直线还
是一条曲线呢?
因为xy=60,所以x与y成反比例关系 曲线
解析:本题要根据平行四边形的面积公式,结合正、反比例关系的定义来解答。
第7课时
比
例
尺(1)
1.
填空。
(1)
一幅图的(
)和(
)的比,叫做这幅图的比例尺。
(2)
为了计算方便,通常把比例尺写成前项或后项是(
)的形式。
(3)
一幅图纸上,5
cm表示实际距离400
m,这幅图纸的比例尺是(
)。
(4)
将线段比例尺
改写成数值比例尺为(
)。
(5)
比例尺1∶400000表示图上距离1
cm代表实际距离(
)cm,也就是
(
)km。
(6)
比例尺是5∶1的平面图上,表示(
)是(
)的5倍。
图上距离
实际距离
1
1∶8000
1∶3000000
400000
4
图上距离
实际距离
2.
判断。
(1)
一幅图的比例尺是500∶1厘米。(?
)
(2)
在一幅图上,如果图上距离是12
cm,实际距离是60
m,那么这幅图的比例
尺是1∶5。(
?)
(3)
这个线段比例尺表示图上距离1
cm相当于实际距离20
m。(?
)
(4)
60∶1这个数值比例尺表示图上距离1
cm相当于实际距离
60
cm。(?
)
(5)
比例尺为1∶1,说明实际距离和图上距离相等。(
?)
3.
选择。
(1)
一种电脑零件的长是5
mm,在设计图上的长度为10
cm,这幅设计图的比例
尺为(
)。
①
1∶2
②
2∶1
③
1∶20
④
20∶1
(2)
一幅图的比例尺是1∶100,它表示图上距离是实际距离的(
)。
①
100倍
②
③
101倍
④
×
×
×
×
√
④
②
(3)
把数值比例尺1∶600000改写成线段比例尺是(
)。
①
②
③
4.
已知甲地到乙地的实际距离是2400
km,如果在一幅地图上量得甲地到乙地的距
离是8
cm,那么这幅地图的比例尺是多少?
2400
km=240000000
cm 8∶240000000=1∶30000000
5.
某地发生爆炸,当地派出所距爆炸点400
m(如图)。
(1)
请你量出图上距离,并计算出这幅图的比例尺。
(2)
将这幅图的线段比例尺补充完整。
量得图上距离为2
cm 400
m=40000
cm 2∶40000=1∶20000
③
200
6.
有一种手机零件非常精密,长度只有0.75
cm,把它画在图纸上却画了7.5
dm。
你能求出这张图纸的比例尺吗?
7.5
dm=75
cm 75∶0.75=100∶1
7.
有三张地图,比例尺分别是1∶2000000,,
。哪一张地图中,
6
cm长的线段表示的实际距离最长?
1
cm∶15
km=1∶1500000 比例尺为的地图中,6
cm长的线段表示的实际距离最长 解析:这是一道关于比例尺的题目,熟练掌握实际距离、图上距离与比例尺之间的关系是解题的关键。
第8课时
比
例
尺(2)
1.
填空。
(1)
图上距离∶(
)=比例尺
实际距离=(
)÷(
)
(2)
在一幅比例尺是1∶200000的平面图上,量得A,B两地的图上距离是8
cm,
那么A,B两地的实际距离是(
)km。
(3)
把一个长为4
mm的零件画在一张比例尺为50∶1的图纸上,需要画(
)cm。
2.
在一幅比例尺是20∶1的生物图纸上,量得一只蚂蚁的长是15
cm,这只蚂蚁的
实际长度是多少厘米?
实际距离
图上距离
比例尺
16
20
15÷20=0.75(cm)
3.
先量出下图中小华从家到学校、少年宫和体育馆的距离(精确到整厘米数),再
根据比例尺分别算出小华从家到学校、少年宫和体育馆的实际距离是多少米?
经测量,可知题图中小华家到学校的距离为1厘米,小华家到少年宫的距离为2厘米,小华家到体育馆的距离为3厘米,所以小华家到学校的实际距离为1÷=200(米);小华家到少年宫的实际距离为2÷=400(米);小华家到体育馆的实际距离为3÷=600(米)
4.
在一幅比例尺是1∶40000000的地图上,量得甲、乙两机场的图上距离是12
cm。
一架客机以800
km/h的速度从甲机场飞往乙机场。
5.
在一幅比例尺是1∶4000的平面图上,量得一块三角形菜地的底是8
cm,底边
上的高是5.5
cm。这块三角形菜地的实际面积是多少平方米?
12÷=480000000(cm) 480000000
cm=4800
km 4800÷800=6(h)
8÷=32000(cm) 32000
cm=320
m 5.5÷=22000(cm)
22000
cm=220
m 320×220×=35200(m2)
6.
在比例尺是1∶500000的地图上,量得A,B两地之间的距离是3.2
cm。在另一
幅地图上,量得这两地之间的距离是2
cm,求另一幅地图的比例尺。
3.2÷=1600000(cm) 2∶1600000=1∶800000 解析:本题要求比例尺,先要求出A,B两地之间的实际距离。
第9课时
比
例
尺(3)
1.
判断。
(1)
比例尺一定,图上距离与实际距离成正比例关系。(
?)
(2)
比例尺中,前项一定小于后项。(
?)
(3)
一幅图的比例尺是1∶300
km。(
?)
2.
填表。
比例尺
图上距离
实际距离
1∶30000
(
)cm
1500
m
(
)
2
cm
300
km
1∶500
28
cm
(
)m
√
×
×
5
1∶15000000
140
3.
李小宇有三张地图,它们的比例尺分别是1∶750000,1∶500000,
,实
际距离是150
km的两地的图上距离在哪张地图上最长?
4.
150
km=15000000
cm 15000000×=20(cm) 15000000×=30(cm) 150÷10=15(cm) 因为30>20>15,所以在比例尺是1∶500000的地图上两地的图上距离最长
100千米=10000000厘米 10000000×=2.5(厘米)
5.
城南社区有一块长125
m、宽75
m的长方形青少年活动场地。请在下面的框内画
出场地的平面图(比例尺是1∶5000),并写出计算过程。
6.
学校的正东方向400
m处是邮局,邮局的正北方向200
m处是广场,广场的正西
方向300
m处是少年宫。先确定比例尺,再画出上述地点的平面图。
长:125
m=12500
cm 12500×=2.5(cm)
宽:75
m=7500
cm 7500×=1.5(cm) 图略
答案不唯一,如比例尺是1∶10000
邮局:400
m=40000
cm 40000×=4(cm) 广场:200
m=20000
cm 20000×=2(cm) 少年宫:300
m=30000
cm 30000×=3(cm)
图略
7.
学校排球场是一个长方形,长是28
m,宽是15
m,把它画在比例尺是1∶100的
图纸上。图纸上的长方形的面积是多少?
长:28
m=2800
cm 2800×=28(cm) 宽:15
m=1500
cm
1500×=15(cm) 28×15=420(cm2)
8.
如图,小明以每分钟50
m的速度从家走到广场需要6分钟。
(1)
他以同样的速度从家走到学校需要多少分钟?
(2)
小明以同样的速度从家往正西方向走5分钟就到了超市,在图中标出超市的
位置。
测量可知题图中小明家到广场的线段长3
cm,小明家到学校的线段长2
cm 50×6=300(m) 300
m=30000
cm 3∶30000=1∶10000 2÷=20000(cm) 20000
cm=200
m 200÷50=4(分)
50×5=250(m) 250
m=25000
cm 25000×=2.5(cm) 图略
第10课时
图形的放大与缩小
1.
填空。
(1)
一个正方形的边长为12
cm,若把它按1∶3缩小,则边长变为(
)cm;若
把它按4∶1放大,则边长变为(
)cm。
(2)
一个直角三角形的两条直角边分别是6
cm、8
cm,如果把它按1∶2缩小,
那么两条直角边分别变成(
)cm和(
)cm;如果按(
)∶(
)放大,
那么两条直角边分别变成18
cm和24
cm。
(3)
图形在放大与缩小过程中,改变的是(
),(
)不变。
2.
判断。
(1)
一个长方形的各边按5∶1放大后,它的面积变为原来的5倍。(
?)
(2)
一个直角三角形的两条直角边都放大为原来的5倍后,斜边也放大为原来的
5倍。(
?)
(3)
一个长、宽比为3∶2的长方形,按2∶1放大后,长、宽比变为6∶2。(?
)
4
48
3
4
3
1
大小
形状
×
√
×
3.
按要求画一画。
(1)
按1∶3画出长方形缩小后的图形。
(2)
按2∶1画出梯形放大后的图形。
4.
先画一画,再观察思考。
(1)
将图形A按4∶1放大,得到新的图形B。
(2)
将图形B按1∶2缩小,得到新的图形C。
(3)
想一想,图形A按(
),就可以得到图形C。
(1)(2)略
略
略
2∶1放大
5.
(1)
图形(
)是图形A放大后的图形,它是按(
)∶(
)放大的。
(2)
图形(
)是图形A缩小后的图形,它是按(
)∶(
)缩小的。
(3)
图形(
)是图形(
)放大后的图形,它是按3∶1放大的。
6.
自己选定比例画图形,把长方形A放大后得到长方形B。观察长方形A和B,它们的面积有什么变化?面积与边长是按相同的比变化的吗?
E
3
2
C
1
2
E
C
略
7.
把下图中左边的三角形按比缩小后得到右边的三角形,求未知数x。(单位:cm)
15∶6=21∶x x=8.4
解析:从图中可以看出两个三角形的短直角边的比值应与长直角边的比值相等。
第11课时
用比例解决问题
1.
填空。
(1)
“小明买4支钢笔用了16元,照这样计算……”这句话中的“照这样计算”
意思是钢笔的(
)是一定的,(
)与(
)成(
)比例关系。
(2)
一列火车从甲地开往乙地,每小时行90
km,4小时到达。如果3小时到达,
那么每小时应行驶多少千米?
①
“从甲地开往乙地”是指(
)一定。
②
(
)与(
)成(
)比例。
③
设每小时应行驶x
km,列比例应为(
)。
单价
总价
数量
正
路程
时间
速度
反
2.
解下面的比例。
3.
小红的身高为1.6
m,她的影子长为2.5
m。如果同一时间,同一地点,测得一
棵树的影子长为4
m,那么这棵树有多高?
4.
实验小学五、六年级的同学们排队做操,每行24人,可以排15行。如果每行20
人,那么可以排多少行?
x=2
x=8
x=1
设这棵树高x
m。 1.6∶2.5=x∶4 x=2.56
设可以排x行。 24×15=20x x=18
5.
一堆煤,原计划每天烧3吨,可以烧72天。改进技术后,每天只烧2.4吨,这堆
煤可以比原来多烧几天?
6.
一列由甲地开往乙地的动车,上午8时从甲地出发,上午11时到达丙地(丙地在
甲、乙两地之间)。甲地到丙地的铁路大约长570
km,甲地到乙地的铁路大约长
1064
km。照这样的速度,从甲地到乙地6小时能到吗?
设这堆煤可以烧x天。
2.4x=72×3 x=90
90-72=18(天)
设从甲地到乙地需要x小时。
570∶(11-8)=1064∶x x=5.6 因为5.6<6,所以6小时能到
7.
张师傅加工一批零件,工作时间(时)与加工零件的数量(个)关系如下图。
(1)
从图上你知道了什么?
(2)
你能提出一个数学问题,并用比例的知识解答吗?
答案不唯一,如张师傅1.5小时加工了45个零件
答案不唯一,如加工100个零件需要多长时间?
设加工100个零件需要x小时。 45∶1.5=100∶x x=
解析:解答本题的关键是充分理解正比例关系在图象上的表示。
第12课时
练
习
课
1.
解比例。
x∶14=0.5∶
0.24∶3=3∶x
2.5∶x=1∶8
=
2.
买20千克橘子的钱,可以买多少千克苹果?
x=35
x=37.5
x=20
x=1350
设可以买x千克苹果。 20×3.5=5x x=14
3.
医药公司需要配制一种药水,药粉和水的质量比是1∶500。
(1)
现有水3000
kg,需要药粉多少千克?
(2)
现要配制这种药水2505
kg,需要加水多少千克?
4.
一艘轮船从A港驶往B港,4
h行驶了160
km。照这样的速度,又行驶了5
h到
达B港。A,B两港相距多远?
5.
学校利用暑假时间给教室铺地。如果用边长为15
cm的方砖铺,那么需要2000
块。如果改用边长为25
cm的方砖铺,那么需要多少块?
设需要药粉x
kg。 x∶3000=1∶500 x=6
设需要加水y
kg。 500∶(1+500)=y∶2505
y=2500
设A,B两港相距x
km。 160∶4=x∶(4+5)
x=360
设如果改用边长为25
cm的方砖铺,那么需要x块。
15×15×2000=25×25×x x=720
6.
舞蹈队有7名男生,24名女生,增加多少名男生,可使男、女生的人数比是5∶3?
7.
如下图,平行四边形ABCD的周长是50
cm,当以AD为底边时,高CE是8
cm;当以
AB为底边时,高CF是12
cm。平行四边形ABCD的面积是多少平方厘米?
设增加x名男生,可使男、女生的人数比为5∶3。
(7+x)∶24=5∶3 x=33
设边AD的长是x
cm,则边AB的长是()cm,即(25-x)cm。
x×8=(25-x)×12 x=15 面积:15×8=120(cm2)[或(25-15)×12=120(cm2)] 解析:本题要抓住平行四边形的两组底和对应的高乘积相等列式。
第13课时
整理与复习
1.
填空。
(1)
已知A×=×B,则B∶A=(
)。
(2)
在一个比例中,两个内项的积是最小的合数,其中一个外项是,另一个外项是(
)。
(3)
如果x=(x,y均不为0),那么x与y成(
)比例关系;如果y=,那么y与x成(
)比例关系。
(4)
两个正方形的边长之比是4∶3,它们的周长之比是(
),面积之比是(
)。
(5)
一张图纸的比例尺是30∶1,一个精密零件的长度是0.2
cm,在图纸上的长度应该是(
)。
4∶5
反
正
4∶3
16∶9
6
cm
(6)
下面的图形(
)是把图形①按1∶2缩小后得到的。
2.
解下面的比例。
∶x=0.4∶
0.8∶x=5∶6
3.
判断下面各题中的两种量是否成比例关系,如果成比例关系,那么成什么比例
关系?填在下面的( )里。
(1)
某班的人数一定,男生人数与女生人数。(
)
(2)
圆柱的体积一定,底面积与高。(
)
(3)
小红从家出发去上学,行走的时间与速度。(
)
(4)
m=5n(m≠0,n≠0),m与n。(
)
(5)
圆的周长一定,π与半径。(
)
④
x=
x=
不成比例关系
成反比例关系
成反比例关系
成正比例关系
不成比例关系
4.
(1)
赵丽看一本书,前6天看了96页,照这样的速度,她看完这本书共用了15
天。这本书共有多少页?
(2)
赵丽看一本书共需24天,每天看16页。如果她要12天看完,那么每天要看
多少页?
5.
在同一幅地图上量得甲、乙两地相距15
cm,甲、丙两地相距20
cm。如果甲、
乙两地实际相距450
km,那么甲、丙两地实际相距多少千米?
设这本书共有x页。 96∶6=x∶15 x=240
设每天要看y页。 24×16=12y y=32
设甲、丙两地实际相距x
km。 15∶450=20∶x
x=600
6.
一根圆柱形木头,小华的叔叔将它锯成4段需要1.2小时。照这样计算,如果把
它锯成10段,那么需要多少小时?
7.
张师傅计划24天加工完一批零件,由于改进了加工方法,实际每天比原计划多
加工20%,这样可以提前几天加工完这批零件?
设需要x小时。 1.2∶(4-1)=x∶(10-1) x=3.6
设可以提前x天加工完这批零件。 24×1=(24-x)×1×(1+20%) x=4
解析:本题中首先要注意工作效率虽然变化了,但工作总量没有变,其次要注意可把原计划的工作效率看作“1”。
自行车的数学
1.
填空。
(1)
一辆自行车,前、后齿轮齿数与它们的转数之间的关系:前齿轮齿数×前齿
轮转数=(
)×(
)。
(2)
自行车蹬一圈走的路程=(
)。
(3)
蹬同样的圈数,前、后齿轮齿数的比值越(
),自行车行走的路程越远。
2.
刘平家的自行车,前齿轮有40个齿,后齿轮有16个齿。如果前齿轮转了12圈,
那么后齿轮应转多少圈?
3.
一辆自行车的前齿轮有48个齿,后齿轮有19个齿,车轮直径是80
cm,蹬一圈能
走多远?(得数保留整数)
后齿轮齿数
后齿轮转数
车轮周长×
大
设后齿轮应转x圈。 40×12=16x x=30
3.14×80×≈635(cm)
4.
一辆自行车的车轮半径是32
cm,前齿轮有30个齿,后齿轮有16个齿。钟鸣家距
离学校大约800
m,他从家到学校大约要蹬多少圈?(得数保留整数)
5.
一辆变速自行车,前齿轮有2个,后齿轮有6个,具体齿数见下表。(先填表,再
解答问题)
(1)
这辆变速自行车能变化出多少种不同的速度?
前齿轮齿数
后齿轮齿数
40
36
32
30
28
26
24
20
2×3.14×32×=376.8(cm) 800
m=80000
cm
80000÷376.8≈212(圈)
2×6=12(种)
5∶4
9∶8
4∶3
6∶5
10∶7
9∶7
20∶13
18∶13
5∶3
3∶2
2∶1
9∶5
前、后齿轮
齿数比
(2)
蹬同样的圈数,要使该变速自行车骑得最远,前、后齿轮齿数比应是多少?
6.
一辆自行车的前齿轮有32个齿,后齿轮有16个齿,蹬一圈自行车前进502.4
cm。
求这辆自行车的车轮直径。
蹬同样的圈数,前、后齿轮齿数比越大,自行车骑得越远,即要使该变速自行车骑得最远,前、后齿轮齿数比应是2∶1
502.4÷(32÷16)÷3.14=80(cm)
4
比
例
第1课时 比例的意义
1.
填空。
(1)
表示(
)相等的(
)叫做比例。
(2)
12∶9的比值是(
),∶的比值是(
),把这两个比写成比例是
(
)。
(3)
写出比值是0.5的两个比是(
)和(
),它们组成的比例是
(
)。
(4)
24的因数有(
),从中选出4个不同的数组成比例
是(
)。
两个比
式子
12∶9=∶
1∶2
2∶4
1∶2=2∶4
(答案不唯一)
1,2,3,4,6,8,12,24
1∶2=3∶6
(最后一空答案不唯一)
2.
选择。
(1)
下面各组比中,能组成比例的是(
)。
①
10∶12
和
24∶36
②
16∶4
和
8∶2
③
∶
和
18∶12
(2)
下面能与∶组成比例的是(
)。
①
6∶8
②
1∶6
③
4∶3
3.
把能组成比例的两个比用线连起来。
7∶14
∶0.8 7.5∶5
7∶12
?
30∶48
∶
∶
8.4∶16.8
②
③
4.
小明买同一种练习本,第一次用4.8元买了6本,第二次用8元买了10本。
(1)
第一次与第二次所用钱数的比是(
),比值是( )。第一次与
第二次所买本数的比是(
),比值是( )。这两个比能组成比例吗?
为什么?
(2)
第一次所用的钱数与买的本数的比是(
),比值是(
)。第
二次所用的钱数与买的本数的比是(
),比值是(
)。这两个比
能组成比例吗?为什么?把组成的比例写出来。
4.8∶8
6∶10
能组成比例 因为它们的比值相等
4.8∶6
0.8
8∶10
0.8
能组成比例 因为它们的比值相等 4.8∶6=8∶10
5.
下面各表中相对应两个量的比能否组成比例?如果能,把组成的比例写出来。
(写出1组)
(1)
(2)
零件总数/个
480
720
时间/时
4
6
已看页数
25
86
未看页数
175
114
能组成比例 答案不唯一,
如480∶4=720∶6
不能组成比例
6.
下面各组中的数可以组成比例吗?如果可以,把组成的比例写出来。(写出1组)
(1)
4,20,5和1
(2)
0.9,12,3.6和0.3
?
?
(3)
,,30和24
(4)
0.5,0.4,和
可以组成比例,答案不唯一,如4∶20=1∶5
不能组成比例
可以组成比例,答案不唯一,如30∶
=24∶
可以组成比例,答案不唯一,
如0.5∶0.4=
∶
7.
先按要求填空,再回答问题。
(1)
图中A,B两个正方形边长的比是(
),周长的比是(
),
这两个比能组成比例吗?
(2)
图中A,B两个正方形面积的比是(
),这个比和边长的比能组成
比例吗?
能组成比例
不能组成比例 解析:注意区分正方形的周长和面积公式。
4∶8
16∶32
16∶64
第2课时
比例的基本性质
1.
填空。
(1)
如果7a=11b(a,b都不为0),那么a∶b=(
)∶(
)。
(2)
在比例中,两个(
)的积等于两个(
)的积,这叫做(
)。
(3)
在比例2∶0.5=1.2∶0.3中,外项是(
)和(
);在比例=中,两
个内项分别是(
)和(
)。
(4)
如果=,那么x×(
)=y×(
)。
(5)
在一个比例中,两个外项互为倒数,若其中一个内项是,则另一个内项是
(
)。
11
7
外项
内项
比例的基本性质
2
0.3
1.2
35
5
4
2.
把能组成比例的两个比连起来。
45:15
10:12
5:8
3.5:
20:32
4:4.8
3.
根据比例的基本性质,在( )里填上合适的数。
(1)
24∶4=(
)∶1
(2)
3∶0.5=1.2∶(
)
(3)
=
(4)
∶(
)=∶
4.
判断。
(1)
在一个比例中,两个外项的积与两个内项的积的差是0。(?
)
(2)
如果0.5∶9=m∶n,那么0.5m=9n。(
?)
(3)
5∶35=1∶7,还可以写成=。(?
)
(4)
在一个比例中,两个内项分别是4和5,两个外项的积一定是20。(
?)
(5)
如果5a=4b(a,b都不为0),那么b∶a=4∶5。(?
)
6
0.2
0.9
√
×
√
√
×
5.
已知3×40=5×24,根据比例的基本性质,把这个等式改写成比例,你能写几
个?把组成的比例写出来。
6.
把8,40,32再配一个数分别满足下面的条件组成比例。
(1)
把8和40同时作为外项(或内项),再配上(
)可以组成比例。
(2)
把8和32同时作为外项(或内项),再配上(
)可以组成比例。
(3)
把40和32同时作为外项(或内项),再配上(
)可以组成比例。
4个 3∶5=24∶40 3∶24=5∶40 5∶3=40∶24 24∶3=40∶5
10
6.4
160
7.
两个比的比值都是6,它们组成的比例的内项都是1.2,写出这个比例。
7.2∶1.2=1.2∶0.2
解析:解题的关键点要理解“它们组成的比例的内项都是1.2”,然后根据“两个比的比值是6”,求第一个比的前项和第二个比的后项。
第3课时
解
比
例
1.
填空。
(1)
解比例的依据是(
)。
(2)
在( )里填上合适的数。
3∶7=5∶(
)
20∶(
)=4∶9
8∶=(
)∶0.5
3.5∶1.4=8.2∶(
)
(3)
将4,5,6再配上一个数组成比例,那么这个数可以是(
)或(
)或(
)。
(4)
如果两个外项的积是最小的合数,其中一个内项是,那么另一个内项是
(
)。
(5)
一项工程,甲单独做10天完成,乙单独做12天完成,甲、乙两人工作效率的
比是(
)∶(
)。
比例的基本性质
45
6
3.28
4.8
7.5
16
6
5
2.
解下面的比例。
x∶45=8∶12
∶=∶x
=
=8∶x
3.
根据下面的条件列出比例,并解比例。
(1)
在一个比例里,两个内项分别是x和0.6,两个外项分别是5.1和1.7。
(2)
0.4与x的比等于3与的比。
(3)
最小的质数与最大的一位数的比等于与x的比。
x=30
x=
x=5
x=36
5.1∶x=0.6∶1.7 x=14.45(列比例不唯一)
0.4∶x=3∶ x=
2∶9=∶x x=
4.
某地上午10时,电线杆的高度与其在地上的影子的长度之比是4∶3。已知影子
的长度是6
m,求电线杆的高度。
5.
有大、小两个圆,大圆的直径是12
cm,大圆的周长与小圆的周长的比是3∶2。
小圆的直径是多少厘米?
6.
某工程队修一条公路,已经修了1800
m,已修的长度与未修的长度的比是3∶5。
这条公路长多少米?
设电线杆的高度为x
m。 x∶6=4∶3 x=8
设小圆的直径为x
cm。 12∶x=3∶2 x=8
设这条公路长x
m。 1800∶x=3∶(5+3) x=4800
7.
音乐兴趣班有男生24人,女生18人,又转入部分女生后,男、女生人数的比是
6∶5。
设转入女生x人。 24∶(18+x)=6∶5 x=2
解析:本题要注意转入的是女生,男生人数不变。
第4课时
正
比
例
1.
填空。
(1)
两种相关联的量,一种量变化,另一种量也随着(
),如果这两种量中
(
)的两个数的(
)一定,这两种量就叫做成正比例的量。
(2)
如果用字母y和x表示两种相关联的量,用k表示它们的比值(
),正比例
关系可以用式子表示为(
)。
(3)
某班订阅《小学生周报》的数量和总价如下表。
①
表中相关联的两种量是(
)和(
),这两种量相对应的两个数的比值都
是(
),这个比值的意义是(
)。
②
因为比值一定,所以表中的两个量叫做成(
)的量。
数量/份
1
2
3
4
5
6
总价/元
1.5
3
4.5
6
7.5
9
变化
相对应
比值
一定
=k
总价
数量
1.5
《小学生周报》的单价
正比例
2.
某品牌雪糕的销售量和销售额的关系如下表。
(1)
写出几组销售额与相对应的销售量的比,并比较比值的大小。
(2)
这个比值表示什么?
(3)
该品牌雪糕的销售额与销售量成正比例关系吗?为什么?
(4)
在下图中描出表示该品牌雪糕的销售额与相对应的销售量的点,然后把这些
点按顺序连接起来。
销售量/箱
4
5
6
7
8
…
销售额/元
240
300
360
420
480
…
240∶4 300∶5 360∶6 420∶7 480∶8 比值相等,都是60
该品牌雪糕的单价
成正比例关系 因为它们的比值固定不变
略
3.
判断下面各题中的两种量是否成正比例关系,是的画“√”,不是的画“×”。
(1)
某种饮料的单价不变,购买饮料的数量与总价。(?
)
(2)
李想的身高与年龄。(?
)
(3)
圆的周长与它的直径。(?
)
(4)
一杯水,喝掉的与剩下的。(?
)
(5)
工作时间一定,工作总量与工作效率。(
?)
√
×
√
×
√
4.
把下表补充完整。
(1)
根据表中的数据,在下图中描出织布的数量和织布的时间所对应的点,再
把它们按顺序连接起来。
(2)
织布的数量与织布的时间成正比例吗?为什么?
(3)
根据图象推算,织布50米需要(
)小时,8小时织布(
)米。
织布的时间/时
1
2
3
5
…
织布的数量/米
20
40
60
80
…
略
成正比例关系 因为织布的数量与织布的时间之间的比值一定
2.5
160
4
100
6.
下表是关于正方体钢块的一些量,哪两种量成正比例关系?(每立方厘米钢块
的质量是一定的)
棱长/cm
1
2
3
4
5
6
底面积/cm2
1
4
9
16
25
36
表面积/cm2
6
24
54
96
150
216
体积/cm3
1
8
27
64
125
216
质量/g
7.8
62.4
210.6
499.2
975
1684.8
表面积与底面积 质量与体积 解析:要求哪两种量成正比例关系就是求这两种量中相对应的两个数的比值一定。
5.
已知y与x成正比例关系,试填写下表。
x
20
60
480
120
y
2.5
6
0.5
0.25
200
0.75
1.5
40
第5课时
反
比
例
1.
填空。
(1)
小明用一定的钱买一种饮料,单价与购买饮料的瓶数的情况如下表。
观察上表我们发现,饮料的瓶数随着(
)的变化而变化。单价增加,饮料的瓶
数(
);单价减少,饮料的瓶数(
)。而且(
)与(
)的
(
)一定,我们就说(
)与(
)成(
)比例关系。
(2)
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系
可以用式子表示为(
)。
(3)
当a+b=2.4时,a与b(
)比例关系;当a·b=2.4时,a与b(
)
比例关系。(填“成”或“不成”)
单价/元
1
2
3
4
数量/瓶
60
30
20
15
单价
减少
增加
单价
饮料的瓶数
乘积
单价
饮料的瓶数
反
xy=k
不成
成
2.
工厂加工一批零件,每小时加工的数量和工作时间如下表。
(1)
每小时加工的数量与工作时间有什么变化规律?
(2)
分别求出各组每小时加工的数量与相对应的工作时间的积,比较积的大小。
(3)
说明这个积所表示的意义。
(4)
每小时加工的数量与相对应的工作时间成反比例关系吗?为什么?
每小时加工的数量/个
10
20
30
40
50
60
工作时间/时
60
30
20
15
12
10
每小时加工的数量随着工作时间的减少而增加
10×60=20×30=30×20=40×15=50×12=60×10=600 积相等,都等于600
这个积表示这批零件的总数量是一定的,为600个
成反比例关系 因为它们的乘积一定
3.
判断下面各题中的两种量是否成反比例关系,是的画“√”,不是的画“×”。
(1)
比的前项一定,比的后项与比值。(
?)
(2)
成活率一定,栽树总棵数与成活棵数。(
?)
(3)
修一条路,工作效率与工作时间。(
?)
(4)
一个人的年龄与体重。(?
)
(5)
路程一定,速度与时间。(?
)
√
×
√
×
√
4.
已知x与y成反比例关系,填写下表。
x
24
6
2.5
…
y
5
15
16
…
5.
看图回答问题。
(1)
速度与时间是否成反比例关系?
(2)
当速度为80
km/h时,所用时间是多少?
速度与时间成反比例关系
10×10÷80=1.25(h)
20
8
48
7.5
6.
已知两种量A,B满足等式×7=×B,A与B成比例关系吗?如果成比例关系,
那么成什么比例关系?
成比例关系 A与B成反比例关系 解析:由×7=×B,可知=,即A×B=7×7=49(一定),所以A与B成比例关系且成反比例关系。
第6课时
练
习
课
1.
填空。
(1)
因为ab=3.2,所以a与b成(
)比例关系。
(2)
若=,则x与y成(
)比例关系。
(3)
因为=y(x,y均不为0),所以x与y成(
)比例关系。
(4)
因为3x=4y,所以x与y成(
)比例关系。
2.
选择。
(1)
圆的周长与(
)成正比例关系。
①
圆的面积
②
圆的直径
③
圆周率
(2)
用地砖铺一间教室,所需地砖的块数与(
)成反比例关系。
①
每块地砖的边长
②
每块地砖的面积
③
每块地砖的周长
反
正
反
正
②
②
(3)
若甲数与乙数互为倒数,则甲数与乙数(
)比例关系。
①
成正
②
成反
③
不成
(4)
下面四句话中,正确的是(
)。
①
三角形的面积一定,它的高与对应的底成正比例关系
②
车轮的周长一定,车轮行驶的路程和转数成反比例关系
③
圆的直径一定,周长和圆周率成正比例关系
④
花生的出油率一定,榨出花生油的质量与花生的质量成正比例关系
②
④
3.
已知表1和表2中x与y分别成正比例关系和反比例关系,请把表格补充完整。
表
1
y
160
130
0.5
x
8
1.5
0.4
表
2
x
3
6
24
y
16
48
8
30
6.5
8
0.025
64
12
32
4
4.
下面的图象表示的是购买甲、乙两种练习本的数量和总价的变化情况。
(1)
两种练习本各买5本,分别需要多少元?
(2)
从图上看,哪种练习本便宜些?
5.
如果=1(b≠0,c≠0),那么:
(1)
当a一定时,b和c成(
)比例关系。
(2)
当b一定时,a和c成(
)比例关系。
(3)
当c一定时,a和b成(
)比例关系。
买5本甲种练习本需要10元,买5本乙种练习本需要5元
乙种练习本便宜些
反
正
正
6.
一个平行四边形的面积是60
cm2,分别用x和y表示它的底和其对应的高,x与y
成什么比例关系?如果把它们的关系用图象表示出来,那么图象是一条直线还
是一条曲线呢?
因为xy=60,所以x与y成反比例关系 曲线
解析:本题要根据平行四边形的面积公式,结合正、反比例关系的定义来解答。
第7课时
比
例
尺(1)
1.
填空。
(1)
一幅图的(
)和(
)的比,叫做这幅图的比例尺。
(2)
为了计算方便,通常把比例尺写成前项或后项是(
)的形式。
(3)
一幅图纸上,5
cm表示实际距离400
m,这幅图纸的比例尺是(
)。
(4)
将线段比例尺
改写成数值比例尺为(
)。
(5)
比例尺1∶400000表示图上距离1
cm代表实际距离(
)cm,也就是
(
)km。
(6)
比例尺是5∶1的平面图上,表示(
)是(
)的5倍。
图上距离
实际距离
1
1∶8000
1∶3000000
400000
4
图上距离
实际距离
2.
判断。
(1)
一幅图的比例尺是500∶1厘米。(?
)
(2)
在一幅图上,如果图上距离是12
cm,实际距离是60
m,那么这幅图的比例
尺是1∶5。(
?)
(3)
这个线段比例尺表示图上距离1
cm相当于实际距离20
m。(?
)
(4)
60∶1这个数值比例尺表示图上距离1
cm相当于实际距离
60
cm。(?
)
(5)
比例尺为1∶1,说明实际距离和图上距离相等。(
?)
3.
选择。
(1)
一种电脑零件的长是5
mm,在设计图上的长度为10
cm,这幅设计图的比例
尺为(
)。
①
1∶2
②
2∶1
③
1∶20
④
20∶1
(2)
一幅图的比例尺是1∶100,它表示图上距离是实际距离的(
)。
①
100倍
②
③
101倍
④
×
×
×
×
√
④
②
(3)
把数值比例尺1∶600000改写成线段比例尺是(
)。
①
②
③
4.
已知甲地到乙地的实际距离是2400
km,如果在一幅地图上量得甲地到乙地的距
离是8
cm,那么这幅地图的比例尺是多少?
2400
km=240000000
cm 8∶240000000=1∶30000000
5.
某地发生爆炸,当地派出所距爆炸点400
m(如图)。
(1)
请你量出图上距离,并计算出这幅图的比例尺。
(2)
将这幅图的线段比例尺补充完整。
量得图上距离为2
cm 400
m=40000
cm 2∶40000=1∶20000
③
200
6.
有一种手机零件非常精密,长度只有0.75
cm,把它画在图纸上却画了7.5
dm。
你能求出这张图纸的比例尺吗?
7.5
dm=75
cm 75∶0.75=100∶1
7.
有三张地图,比例尺分别是1∶2000000,,
。哪一张地图中,
6
cm长的线段表示的实际距离最长?
1
cm∶15
km=1∶1500000 比例尺为的地图中,6
cm长的线段表示的实际距离最长 解析:这是一道关于比例尺的题目,熟练掌握实际距离、图上距离与比例尺之间的关系是解题的关键。
第8课时
比
例
尺(2)
1.
填空。
(1)
图上距离∶(
)=比例尺
实际距离=(
)÷(
)
(2)
在一幅比例尺是1∶200000的平面图上,量得A,B两地的图上距离是8
cm,
那么A,B两地的实际距离是(
)km。
(3)
把一个长为4
mm的零件画在一张比例尺为50∶1的图纸上,需要画(
)cm。
2.
在一幅比例尺是20∶1的生物图纸上,量得一只蚂蚁的长是15
cm,这只蚂蚁的
实际长度是多少厘米?
实际距离
图上距离
比例尺
16
20
15÷20=0.75(cm)
3.
先量出下图中小华从家到学校、少年宫和体育馆的距离(精确到整厘米数),再
根据比例尺分别算出小华从家到学校、少年宫和体育馆的实际距离是多少米?
经测量,可知题图中小华家到学校的距离为1厘米,小华家到少年宫的距离为2厘米,小华家到体育馆的距离为3厘米,所以小华家到学校的实际距离为1÷=200(米);小华家到少年宫的实际距离为2÷=400(米);小华家到体育馆的实际距离为3÷=600(米)
4.
在一幅比例尺是1∶40000000的地图上,量得甲、乙两机场的图上距离是12
cm。
一架客机以800
km/h的速度从甲机场飞往乙机场。
5.
在一幅比例尺是1∶4000的平面图上,量得一块三角形菜地的底是8
cm,底边
上的高是5.5
cm。这块三角形菜地的实际面积是多少平方米?
12÷=480000000(cm) 480000000
cm=4800
km 4800÷800=6(h)
8÷=32000(cm) 32000
cm=320
m 5.5÷=22000(cm)
22000
cm=220
m 320×220×=35200(m2)
6.
在比例尺是1∶500000的地图上,量得A,B两地之间的距离是3.2
cm。在另一
幅地图上,量得这两地之间的距离是2
cm,求另一幅地图的比例尺。
3.2÷=1600000(cm) 2∶1600000=1∶800000 解析:本题要求比例尺,先要求出A,B两地之间的实际距离。
第9课时
比
例
尺(3)
1.
判断。
(1)
比例尺一定,图上距离与实际距离成正比例关系。(
?)
(2)
比例尺中,前项一定小于后项。(
?)
(3)
一幅图的比例尺是1∶300
km。(
?)
2.
填表。
比例尺
图上距离
实际距离
1∶30000
(
)cm
1500
m
(
)
2
cm
300
km
1∶500
28
cm
(
)m
√
×
×
5
1∶15000000
140
3.
李小宇有三张地图,它们的比例尺分别是1∶750000,1∶500000,
,实
际距离是150
km的两地的图上距离在哪张地图上最长?
4.
150
km=15000000
cm 15000000×=20(cm) 15000000×=30(cm) 150÷10=15(cm) 因为30>20>15,所以在比例尺是1∶500000的地图上两地的图上距离最长
100千米=10000000厘米 10000000×=2.5(厘米)
5.
城南社区有一块长125
m、宽75
m的长方形青少年活动场地。请在下面的框内画
出场地的平面图(比例尺是1∶5000),并写出计算过程。
6.
学校的正东方向400
m处是邮局,邮局的正北方向200
m处是广场,广场的正西
方向300
m处是少年宫。先确定比例尺,再画出上述地点的平面图。
长:125
m=12500
cm 12500×=2.5(cm)
宽:75
m=7500
cm 7500×=1.5(cm) 图略
答案不唯一,如比例尺是1∶10000
邮局:400
m=40000
cm 40000×=4(cm) 广场:200
m=20000
cm 20000×=2(cm) 少年宫:300
m=30000
cm 30000×=3(cm)
图略
7.
学校排球场是一个长方形,长是28
m,宽是15
m,把它画在比例尺是1∶100的
图纸上。图纸上的长方形的面积是多少?
长:28
m=2800
cm 2800×=28(cm) 宽:15
m=1500
cm
1500×=15(cm) 28×15=420(cm2)
8.
如图,小明以每分钟50
m的速度从家走到广场需要6分钟。
(1)
他以同样的速度从家走到学校需要多少分钟?
(2)
小明以同样的速度从家往正西方向走5分钟就到了超市,在图中标出超市的
位置。
测量可知题图中小明家到广场的线段长3
cm,小明家到学校的线段长2
cm 50×6=300(m) 300
m=30000
cm 3∶30000=1∶10000 2÷=20000(cm) 20000
cm=200
m 200÷50=4(分)
50×5=250(m) 250
m=25000
cm 25000×=2.5(cm) 图略
第10课时
图形的放大与缩小
1.
填空。
(1)
一个正方形的边长为12
cm,若把它按1∶3缩小,则边长变为(
)cm;若
把它按4∶1放大,则边长变为(
)cm。
(2)
一个直角三角形的两条直角边分别是6
cm、8
cm,如果把它按1∶2缩小,
那么两条直角边分别变成(
)cm和(
)cm;如果按(
)∶(
)放大,
那么两条直角边分别变成18
cm和24
cm。
(3)
图形在放大与缩小过程中,改变的是(
),(
)不变。
2.
判断。
(1)
一个长方形的各边按5∶1放大后,它的面积变为原来的5倍。(
?)
(2)
一个直角三角形的两条直角边都放大为原来的5倍后,斜边也放大为原来的
5倍。(
?)
(3)
一个长、宽比为3∶2的长方形,按2∶1放大后,长、宽比变为6∶2。(?
)
4
48
3
4
3
1
大小
形状
×
√
×
3.
按要求画一画。
(1)
按1∶3画出长方形缩小后的图形。
(2)
按2∶1画出梯形放大后的图形。
4.
先画一画,再观察思考。
(1)
将图形A按4∶1放大,得到新的图形B。
(2)
将图形B按1∶2缩小,得到新的图形C。
(3)
想一想,图形A按(
),就可以得到图形C。
(1)(2)略
略
略
2∶1放大
5.
(1)
图形(
)是图形A放大后的图形,它是按(
)∶(
)放大的。
(2)
图形(
)是图形A缩小后的图形,它是按(
)∶(
)缩小的。
(3)
图形(
)是图形(
)放大后的图形,它是按3∶1放大的。
6.
自己选定比例画图形,把长方形A放大后得到长方形B。观察长方形A和B,它们的面积有什么变化?面积与边长是按相同的比变化的吗?
E
3
2
C
1
2
E
C
略
7.
把下图中左边的三角形按比缩小后得到右边的三角形,求未知数x。(单位:cm)
15∶6=21∶x x=8.4
解析:从图中可以看出两个三角形的短直角边的比值应与长直角边的比值相等。
第11课时
用比例解决问题
1.
填空。
(1)
“小明买4支钢笔用了16元,照这样计算……”这句话中的“照这样计算”
意思是钢笔的(
)是一定的,(
)与(
)成(
)比例关系。
(2)
一列火车从甲地开往乙地,每小时行90
km,4小时到达。如果3小时到达,
那么每小时应行驶多少千米?
①
“从甲地开往乙地”是指(
)一定。
②
(
)与(
)成(
)比例。
③
设每小时应行驶x
km,列比例应为(
)。
单价
总价
数量
正
路程
时间
速度
反
2.
解下面的比例。
3.
小红的身高为1.6
m,她的影子长为2.5
m。如果同一时间,同一地点,测得一
棵树的影子长为4
m,那么这棵树有多高?
4.
实验小学五、六年级的同学们排队做操,每行24人,可以排15行。如果每行20
人,那么可以排多少行?
x=2
x=8
x=1
设这棵树高x
m。 1.6∶2.5=x∶4 x=2.56
设可以排x行。 24×15=20x x=18
5.
一堆煤,原计划每天烧3吨,可以烧72天。改进技术后,每天只烧2.4吨,这堆
煤可以比原来多烧几天?
6.
一列由甲地开往乙地的动车,上午8时从甲地出发,上午11时到达丙地(丙地在
甲、乙两地之间)。甲地到丙地的铁路大约长570
km,甲地到乙地的铁路大约长
1064
km。照这样的速度,从甲地到乙地6小时能到吗?
设这堆煤可以烧x天。
2.4x=72×3 x=90
90-72=18(天)
设从甲地到乙地需要x小时。
570∶(11-8)=1064∶x x=5.6 因为5.6<6,所以6小时能到
7.
张师傅加工一批零件,工作时间(时)与加工零件的数量(个)关系如下图。
(1)
从图上你知道了什么?
(2)
你能提出一个数学问题,并用比例的知识解答吗?
答案不唯一,如张师傅1.5小时加工了45个零件
答案不唯一,如加工100个零件需要多长时间?
设加工100个零件需要x小时。 45∶1.5=100∶x x=
解析:解答本题的关键是充分理解正比例关系在图象上的表示。
第12课时
练
习
课
1.
解比例。
x∶14=0.5∶
0.24∶3=3∶x
2.5∶x=1∶8
=
2.
买20千克橘子的钱,可以买多少千克苹果?
x=35
x=37.5
x=20
x=1350
设可以买x千克苹果。 20×3.5=5x x=14
3.
医药公司需要配制一种药水,药粉和水的质量比是1∶500。
(1)
现有水3000
kg,需要药粉多少千克?
(2)
现要配制这种药水2505
kg,需要加水多少千克?
4.
一艘轮船从A港驶往B港,4
h行驶了160
km。照这样的速度,又行驶了5
h到
达B港。A,B两港相距多远?
5.
学校利用暑假时间给教室铺地。如果用边长为15
cm的方砖铺,那么需要2000
块。如果改用边长为25
cm的方砖铺,那么需要多少块?
设需要药粉x
kg。 x∶3000=1∶500 x=6
设需要加水y
kg。 500∶(1+500)=y∶2505
y=2500
设A,B两港相距x
km。 160∶4=x∶(4+5)
x=360
设如果改用边长为25
cm的方砖铺,那么需要x块。
15×15×2000=25×25×x x=720
6.
舞蹈队有7名男生,24名女生,增加多少名男生,可使男、女生的人数比是5∶3?
7.
如下图,平行四边形ABCD的周长是50
cm,当以AD为底边时,高CE是8
cm;当以
AB为底边时,高CF是12
cm。平行四边形ABCD的面积是多少平方厘米?
设增加x名男生,可使男、女生的人数比为5∶3。
(7+x)∶24=5∶3 x=33
设边AD的长是x
cm,则边AB的长是()cm,即(25-x)cm。
x×8=(25-x)×12 x=15 面积:15×8=120(cm2)[或(25-15)×12=120(cm2)] 解析:本题要抓住平行四边形的两组底和对应的高乘积相等列式。
第13课时
整理与复习
1.
填空。
(1)
已知A×=×B,则B∶A=(
)。
(2)
在一个比例中,两个内项的积是最小的合数,其中一个外项是,另一个外项是(
)。
(3)
如果x=(x,y均不为0),那么x与y成(
)比例关系;如果y=,那么y与x成(
)比例关系。
(4)
两个正方形的边长之比是4∶3,它们的周长之比是(
),面积之比是(
)。
(5)
一张图纸的比例尺是30∶1,一个精密零件的长度是0.2
cm,在图纸上的长度应该是(
)。
4∶5
反
正
4∶3
16∶9
6
cm
(6)
下面的图形(
)是把图形①按1∶2缩小后得到的。
2.
解下面的比例。
∶x=0.4∶
0.8∶x=5∶6
3.
判断下面各题中的两种量是否成比例关系,如果成比例关系,那么成什么比例
关系?填在下面的( )里。
(1)
某班的人数一定,男生人数与女生人数。(
)
(2)
圆柱的体积一定,底面积与高。(
)
(3)
小红从家出发去上学,行走的时间与速度。(
)
(4)
m=5n(m≠0,n≠0),m与n。(
)
(5)
圆的周长一定,π与半径。(
)
④
x=
x=
不成比例关系
成反比例关系
成反比例关系
成正比例关系
不成比例关系
4.
(1)
赵丽看一本书,前6天看了96页,照这样的速度,她看完这本书共用了15
天。这本书共有多少页?
(2)
赵丽看一本书共需24天,每天看16页。如果她要12天看完,那么每天要看
多少页?
5.
在同一幅地图上量得甲、乙两地相距15
cm,甲、丙两地相距20
cm。如果甲、
乙两地实际相距450
km,那么甲、丙两地实际相距多少千米?
设这本书共有x页。 96∶6=x∶15 x=240
设每天要看y页。 24×16=12y y=32
设甲、丙两地实际相距x
km。 15∶450=20∶x
x=600
6.
一根圆柱形木头,小华的叔叔将它锯成4段需要1.2小时。照这样计算,如果把
它锯成10段,那么需要多少小时?
7.
张师傅计划24天加工完一批零件,由于改进了加工方法,实际每天比原计划多
加工20%,这样可以提前几天加工完这批零件?
设需要x小时。 1.2∶(4-1)=x∶(10-1) x=3.6
设可以提前x天加工完这批零件。 24×1=(24-x)×1×(1+20%) x=4
解析:本题中首先要注意工作效率虽然变化了,但工作总量没有变,其次要注意可把原计划的工作效率看作“1”。
自行车的数学
1.
填空。
(1)
一辆自行车,前、后齿轮齿数与它们的转数之间的关系:前齿轮齿数×前齿
轮转数=(
)×(
)。
(2)
自行车蹬一圈走的路程=(
)。
(3)
蹬同样的圈数,前、后齿轮齿数的比值越(
),自行车行走的路程越远。
2.
刘平家的自行车,前齿轮有40个齿,后齿轮有16个齿。如果前齿轮转了12圈,
那么后齿轮应转多少圈?
3.
一辆自行车的前齿轮有48个齿,后齿轮有19个齿,车轮直径是80
cm,蹬一圈能
走多远?(得数保留整数)
后齿轮齿数
后齿轮转数
车轮周长×
大
设后齿轮应转x圈。 40×12=16x x=30
3.14×80×≈635(cm)
4.
一辆自行车的车轮半径是32
cm,前齿轮有30个齿,后齿轮有16个齿。钟鸣家距
离学校大约800
m,他从家到学校大约要蹬多少圈?(得数保留整数)
5.
一辆变速自行车,前齿轮有2个,后齿轮有6个,具体齿数见下表。(先填表,再
解答问题)
(1)
这辆变速自行车能变化出多少种不同的速度?
前齿轮齿数
后齿轮齿数
40
36
32
30
28
26
24
20
2×3.14×32×=376.8(cm) 800
m=80000
cm
80000÷376.8≈212(圈)
2×6=12(种)
5∶4
9∶8
4∶3
6∶5
10∶7
9∶7
20∶13
18∶13
5∶3
3∶2
2∶1
9∶5
前、后齿轮
齿数比
(2)
蹬同样的圈数,要使该变速自行车骑得最远,前、后齿轮齿数比应是多少?
6.
一辆自行车的前齿轮有32个齿,后齿轮有16个齿,蹬一圈自行车前进502.4
cm。
求这辆自行车的车轮直径。
蹬同样的圈数,前、后齿轮齿数比越大,自行车骑得越远,即要使该变速自行车骑得最远,前、后齿轮齿数比应是2∶1
502.4÷(32÷16)÷3.14=80(cm)
