六年级下册数学习题课件-3 圆柱与圆锥 人教版(共43张PPT)
文档属性
| 名称 | 六年级下册数学习题课件-3 圆柱与圆锥 人教版(共43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览






文档简介
(共43张PPT)
3
圆柱和圆锥
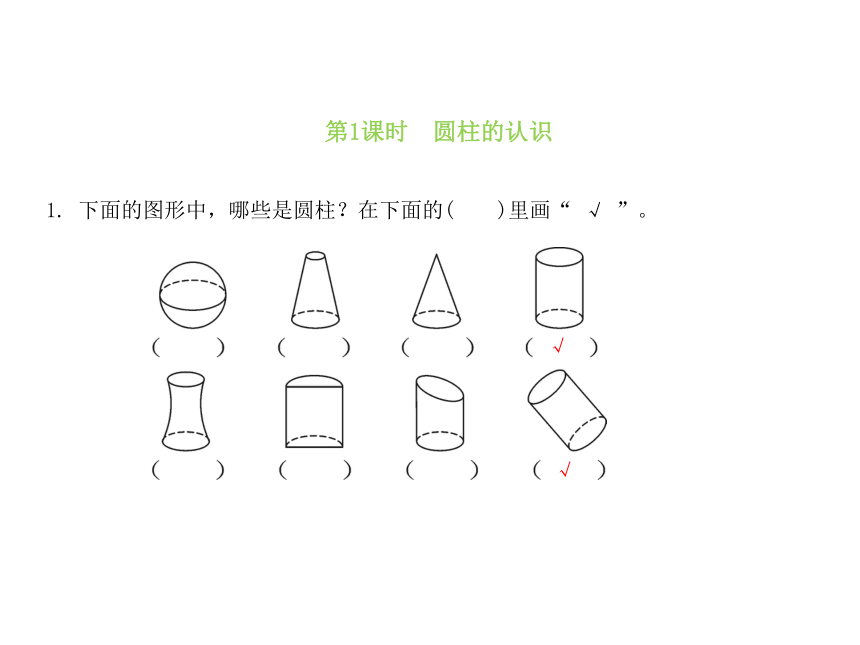
第1课时 圆柱的认识
1.
下面的图形中,哪些是圆柱?在下面的( )里画“
√
”。
√
√
2.
标出下面圆柱的高、底面、侧面。
3.
填空。
(1)
用一张长31.4
cm、宽15.7
cm的长方形厚纸板围成圆柱,有(
)种围法。
其中一种圆柱的高是(
)cm,底面直径是(
)cm;另一种圆柱的高是
(
)cm,底面直径是(
)cm。
(2)
把圆柱的侧面展开得到一个(
),这个(
)的长等于
圆柱的(
),宽等于圆柱的(
)。
(3)
当圆柱的(
)和(
)相等时,它的侧面沿高展开后是一个正
方形。
(4)
圆柱有(
)条高。
略
两
31.4
5
15.7
10
长方形
长方形
底面周长
高
高
底面周长
无数
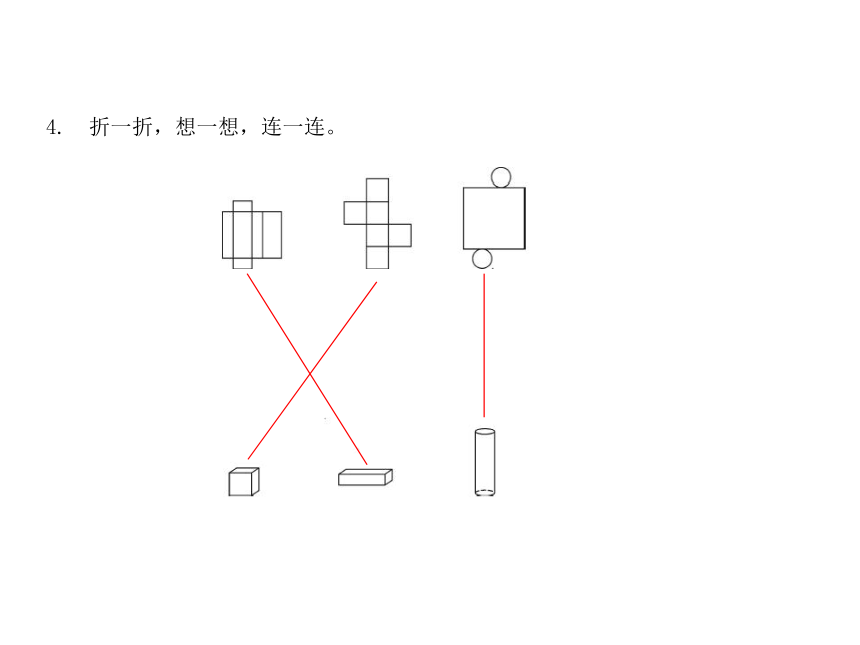
4.
折一折,想一想,连一连。
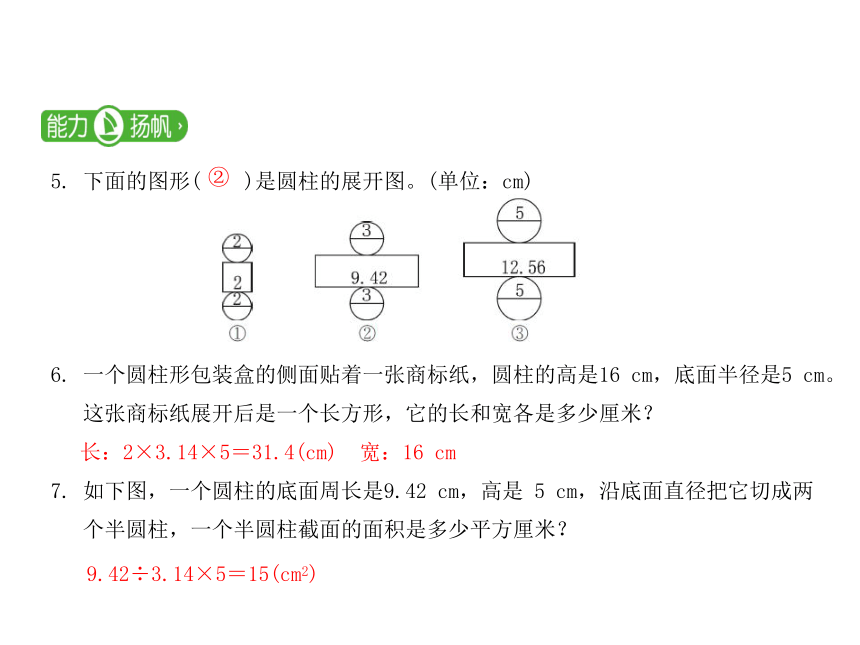
5.
下面的图形(
)是圆柱的展开图。(单位:cm)
6.
一个圆柱形包装盒的侧面贴着一张商标纸,圆柱的高是16
cm,底面半径是5
cm。
这张商标纸展开后是一个长方形,它的长和宽各是多少厘米?
7.
如下图,一个圆柱的底面周长是9.42
cm,高是
5
cm,沿底面直径把它切成两
个半圆柱,一个半圆柱截面的面积是多少平方厘米?
②
长:2×3.14×5=31.4(cm) 宽:16
cm
9.42÷3.14×5=15(cm2)
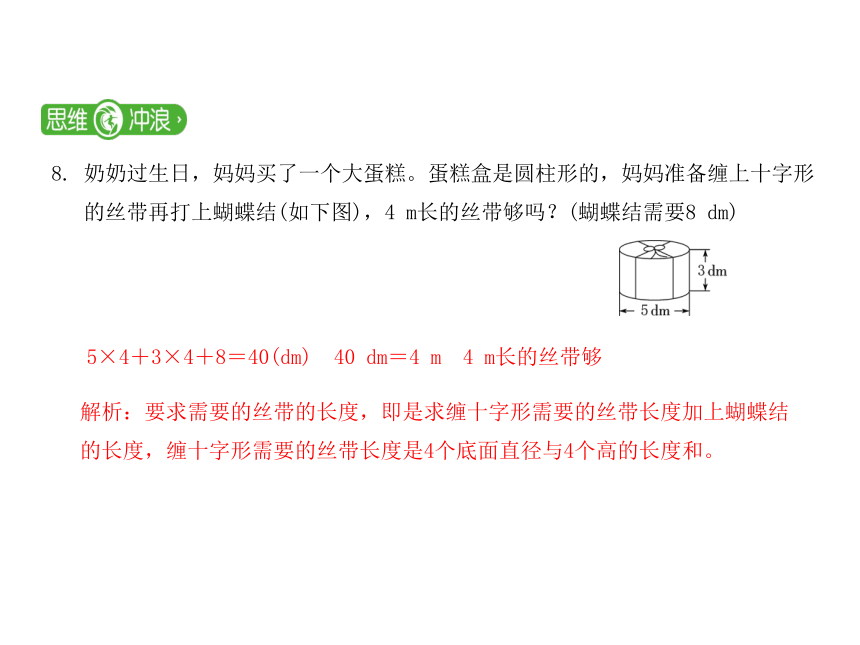
8.
奶奶过生日,妈妈买了一个大蛋糕。蛋糕盒是圆柱形的,妈妈准备缠上十字形
的丝带再打上蝴蝶结(如下图),4
m长的丝带够吗?(蝴蝶结需要8
dm)
5×4+3×4+8=40(dm) 40
dm=4
m 4
m长的丝带够
解析:要求需要的丝带的长度,即是求缠十字形需要的丝带长度加上蝴蝶结的长度,缠十字形需要的丝带长度是4个底面直径与4个高的长度和。
第2课时
圆柱的表面积
1.
填空。
(1)
圆柱的表面积=(
)+(
)×2
圆柱的侧面积=(
)×(
)
(2)
一个圆柱的侧面积是50.24
dm2,高是4
dm,它的底面周长是(
)dm,
直径是(
)dm,底面积是(
)dm2。
(3)
一个圆柱的底面直径是6
cm,高是8
cm,它的侧面积是(
)cm2,
表面积是(
)cm2。
2.
计算下面各圆柱的底面积和侧面积。
(1)
底面半径是0.4
m,高是5
m。
圆柱的侧面积
底面积
底面周长
高
12.56
4
12.56
150.72
207.24
底面积:3.14×0.42=0.5024(m2) 侧面积:2×3.14×0.4×5=12.56(m2)
(2)
底面周长是18.84
cm,高是4
cm。
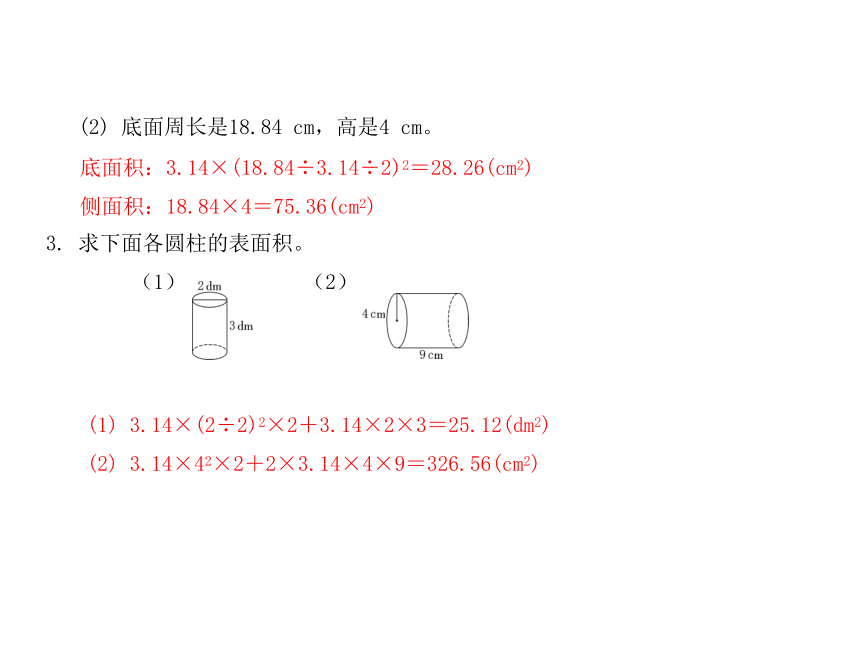
3.
求下面各圆柱的表面积。
(1)
(2)
(1)
3.14×(2÷2)2×2+3.14×2×3=25.12(dm2)
(2)
3.14×42×2+2×3.14×4×9=326.56(cm2)
底面积:3.14×(18.84÷3.14÷2)2=28.26(cm2)
侧面积:18.84×4=75.36(cm2)
4.
某建筑的中央有4根同样大小的圆柱形龙柱,它的高是19.2
m,底面直径是
1.2
m。如果在每根龙柱的表面刷一层油漆,那么刷油漆部分的面积是多少平
方米?(提示:只刷龙柱的侧面)
5.
一台压路机的滚筒宽1.5
m,直径是1
m。如果它每分钟滚动10周,那么滚动1
分钟,压过的面积是多少平方米?
3.14×1.2×19.2×4=289.3824(m2)
3.14×1×1.5×10=47.1(m2)
6.
一种圆柱形饮料瓶的底面周长是18.84
cm,高是10
cm,饮料的包装纸箱如下图,
你能算出这个纸箱的容积吗?
18.84÷3.14=6(cm) (6×6)×(6×4)×10=8640(cm3)
7.
一根圆柱形的小棒,底面直径是2
cm,高是15
cm。
(1)
把它沿着底面直径切成两个半圆柱,它的表面积增加了多少?
(2)
如果把它从正中间横切成两个相同的小圆柱,那么它的表面积增加了多少?
2×15×2=60(cm2)
解析:求增加的表面积就是求切开后两个半圆柱截面(长方形)的面积。
3.14×(2÷2)2×2=6.28(cm2)
解析:求增加的表面积就是求两个小圆柱的底面积。
第3课时
练
习
课
1.
下面的问题实际求的是什么?把问题前的字母填在相应的( )里。
A.
做圆柱形通风管需要的铁皮
B.
圆柱形水池的占地面积
C.
压路机滚筒转动一周压路的面积
D.
做有盖的圆柱形油桶需要的铁皮
E.
做圆柱形笔筒需要的纸板
(1)
求侧面积。(
)
(2)
求底面积。(
)
(3)
求表面积。(
)
(4)
求一个底面积与侧面积的和。(
)
A,C
B
D
E
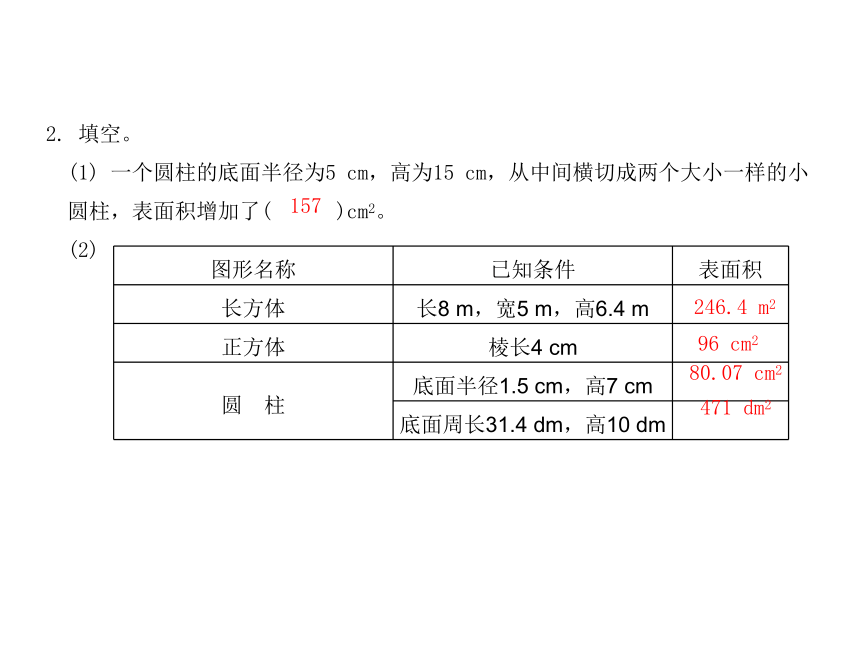
2.
填空。
(1)
一个圆柱的底面半径为5
cm,高为15
cm,从中间横切成两个大小一样的小
圆柱,表面积增加了(
)cm2。
(2)
图形名称
已知条件
表面积
长方体
长8
m,宽5
m,高6.4
m
正方体
棱长4
cm
圆 柱
底面半径1.5
cm,高7
cm
?
底面周长31.4
dm,高10
dm
?
157
246.4
m2
96
cm2
80.07
cm2
471
dm2
3.
选择。
(1)
甲、乙两人用不同的方法分别将一张长20
cm、宽15
cm的纸围成一个圆柱
(接头处不重叠),则围成的圆柱的(
)。
①
高相等
②
侧面积相等
③
侧面积和高都相等
④
侧面积和高都不相等
(2)
有一个圆柱,按如下图所示的方式截成3段,增加了(
)个底面。
①
2
②
3
③
4
(3)
一个圆柱的高是25.12
cm,它的侧面展开图是一个正方形,它的底面半径
是(
)cm。
①
25.12
②
8
③
4
④
16
②
③
③
4.
有一个圆柱形蓄水池,底面半径为2
m,深3
m。在池底和池壁抹上水泥,如果
每平方米用水泥20
kg,那么一共要用水泥多少千克?
5.
计算下面图形的表面积。
6.
有一根圆柱形木棒,准备将它的表面刷上油漆。如果1
g油漆能刷5
cm2,那么
当这根木棒的底面半径为3
cm,长为2
m时,需要油漆多少克?
2×3.14×2×3+3.14×22=50.24(m2) 20×50.24=1004.8(kg)
3.14×2×10+(5×8+2×8+2×5)×2=194.8(dm2)
2
m=200
cm 2×3.14×3×200+3.14×32×2=3824.52(cm2)
3824.52÷5=764.904(g)
7.
如下图,把一根长60
cm的圆柱形木料截去10
cm长的一段,表面积就减少了
502.4
cm2。原来这根圆柱形木料的表面积是多少平方厘米?
直径:502.4÷10÷3.14=16(cm)
表面积:3.14×(16÷2)2×2+502.4×(60÷10)=3416.32(cm2)
解析:底面积没变,减少的502.4
cm2就是侧面积减少的部分,即可求出这根木料的底面直径,从而求出它的底面积,侧面积是减少的侧面积的(60÷10)倍。
第4课时
圆柱的体积
1.
填空。
(1)
如下图,把圆柱的底面分成许多个相等的扇形,然后把圆
柱切开,可以拼成一个近似的(
)体,这个(
)体的
底面积等于圆柱的(
),高等于圆柱的(
),长方体的体积等于
(
)乘(
),所以圆柱的体积的计算公式是(
)。
(2)
一个圆柱的底面半径是4
dm,高是4
dm,这个圆柱的体积是(
)dm3。
(3)
若圆柱的底面积扩大为原来的4倍,高扩大为原来的2倍,则体积扩大为原
来的(
)倍。
(4)
长方体、正方体和圆柱的体积都可以用(
)来计算。
(5)
7.5
dm3=(
)L=(
)mL
230
cm3=(
)mL=(
)L
长方
长方
底面积
高
底面积
高
圆柱的体积=底面积×高
200.96
8
体积=底面积×高
7.5
7500
230
0.23
2.
看图计算下面圆柱的体积。
(1)
(2)
3.
两个底面积相等的圆柱,一个圆柱的高是7
dm,体积是63
dm3;另一个圆柱的
高是5
dm,它的体积是多少立方分米?
3.14×(20÷2)2×40=12560(cm3)
5×18=90(cm3)
63÷7×5=45(dm3)
4.
一个圆柱形电饭煲,从里面量得底面周长是9.42
dm,高是2.8
dm。这个电饭
煲的容积大约是多少升?(得数保留整数)
5.
一辆油罐车的油罐是圆柱形的,底面直径是3
m,长是5
m。如果每立方米可装
汽油0.8
t,那么这辆油罐车最多可装汽油多少吨?
6.
如下图,这个杯子能装下这盒牛奶吗?(不计杯壁的厚度)(单位:cm)
3.14×(9.42÷3.14÷2)2×2.8=19.782(dm3)
19.782
dm3≈20
L
3.14×(3÷2)2×5×0.8=28.26(t)
3.14×(6÷2)2×8=226.08(cm3)
226.08
cm3=226.08
mL
因为226.08>225,所以这个杯子能装下这盒牛奶
7.
把一根长1.5
m的圆柱形钢材截成3段后如下图所示,表面积比原来增加9.6
dm2。
这根钢材原来的体积是多少立方分米?
1.5
m=15
dm 9.6÷[(3-1)×2]×15=36(dm3)
解析:解题的关键是求出这根钢材的底面积,钢材的底面积=增加的表面积÷增加的底面个数。
第5课时
解决实际问题
1.
填空。
(1)
我们常常利用(
)的特性,把不规则图形转化成(
)
来计算。
(2)
右图中,将图①的瓶子倒置变成图②,瓶子中水的体积不变,所以图①和图
②空置部分的体积(
)。由此可以将图①的空置部分转化成一个高是
(
)cm的圆柱形。要求瓶子的容积可以先根据图①求出(
)的体积,再根据图②
求出(
)的体积,两者相加就是瓶子的容积了。
(3)
把一个棱长为4分米的正方体木块削成一个最大的圆柱,这个圆柱的体积是
(
)立方分米。
(4)
加工厂将一块棱长为3
dm的正方体铁块熔铸成一个圆柱形零件,这个零件的
体积是(
)dm3。
体积不变
规则图形
相等
20
水
空置部分
50.24
27
2.
一个圆柱形粮囤,从里面量底面半径是3
m,高是2
m,这个粮囤最多能装粮多
少立方米?
3.
有一个长方体铁块的长是9
dm,宽是5
dm,高是3.14
dm。把它熔铸成一个底面
半径是3
dm的圆柱形铁块,这个圆柱形铁块的高是多少分米?
3.14×32×2=56.52(m3)
(9×5×3.14)÷(3.14×32)=5(dm)
4.
一个瓶子的高度是30
cm,底面内直径是8
cm,瓶子里的水的高度是20
cm(如
图①)。把瓶子倒置,这时水的高度是24
cm(如图②)。这个瓶子的容积是多少?
5.
一个水龙头的内直径是1.6
cm,打开水龙头后水的流速是30
cm/s。一个容积
是5
L的水桶,80
s能装满水吗?
6.
一个圆柱形水槽里面盛有10
cm深的水,水槽的底面积为200
cm2。现将一个棱
长为5
cm的正方体铁块放入水中(铁块完全浸没水中),水面将上升至多少厘米?
3.14×(8÷2)2×(30-24+20)=1306.24(cm3)
1306.24
cm3=1306.24
mL
3.14×(1.6÷2)2×30×80=4823.04(cm3) 4823.04
cm3=4.82304
L 因为4.82304<5,所以80
s不能装满水
5×5×5÷200+10=10.625(cm)
7.
如下图是一根底面直径是6
cm的圆柱形木料被斜着截去一段后剩下的部分。求
剩下的部分的体积。
3.14×(6÷2)2×(8+10)÷2=254.34(cm3)
解析:解答本题的关键是理解剩下的部分的体积是底面直径为6
cm、高为(8+10)cm的圆柱形体积的一半。
第6课时
练
习
课
1.
选择。
(1)
圆柱的高不变,若底面半径扩大为原来的3倍,则体积应该(
)。
①
扩大为原来的3倍
②
扩大为原来的6倍
③
扩大为原来的9倍
④
不变
(2)
等底等高的圆柱、正方体、长方体的体积相比较,(
)。
①
正方体的体积大
②
长方体的体积大
③
一样大
(3)
有甲、乙两个等底的圆柱,如果甲圆柱的高是乙圆柱高的,那么甲圆柱的
体积是乙圆柱体积的(
)。
①
②
③
(4)
求一个圆柱形水桶能盛多少水,就是求水桶的(
)。
①
表面积
②
体积
③
容积
③
③
②
③
2.
填表。
底面半径/m
底面直径/m
高/m
圆柱的表面积/m2
圆柱的体积/m3
10
6
14
5
3
141.3
3.
如下图,这根钢管长50
m,每立方厘米的钢管重
8
g,这根钢管重多少千克?
7
20
6
5
1004.8
527.52
150.72
1884
769.3
50
m=5000
cm 3.14××5000×8=879200(g)
879200
g=879.2
kg
4.
赵雪家有15个底面积是40
cm2、高是10
cm的圆柱形水杯,一壶水正好能倒满3
杯。如果让12位客人都能喝上这壶水,那么平均每杯倒多少毫升?
5.
一根圆柱形水管,内直径是20
cm,水流的速度是5
m/s。这根水管每分钟最多
流过多少立方米的水?
6.
有一张长方形的纸,长是24
cm,宽是12
cm,分别以它的长和宽所在直线为轴
旋转一周,得到两个圆柱体,它们的体积差是多少?
40×10×3÷12=100(cm3) 100
cm3=100
mL
20
cm=0.2
m 3.14×(0.2÷2)2×5×60=9.42(m3)
3.14×242×12-3.14×122×24=10851.84(cm3)
7.
下面4个图形的面积都是100
cm2,用这些图形分别卷成圆柱,哪个圆柱的体积
最大?哪个圆柱的体积最小?你有什么发现?(单位:cm,圆柱的底面周长等于
长方形的长,得数保留整数)
图形①:3.14×(50÷3.14÷2)2×2≈398(cm3)
图形②:3.14×(25÷3.14÷2)2×4≈199(cm3)
图形③:3.14×(20÷3.14÷2)2×5≈159(cm3)
图形④:3.14×(10÷3.14÷2)2×10≈80(cm3)
因为80<159<199<398,所以图形①卷成的圆柱的体积最大,图形④卷成的圆柱的体积最小 发现:面积相等的长方形或正方形,以长方形的长为圆柱的底面周长,长方形的长和宽的差距越大,卷成的圆柱的体积则越大;长方形的长和宽的差距越小,卷成的圆柱的体积则越小(合理即可) 解析:分别求出4个图形卷成圆柱的底面半径,再分别求出它们的体积进行比较。
第7课时
圆锥的认识
1.
填空。
(1)
圆锥的底面是个(
),从圆锥的顶点到底面圆心的距离是圆锥的(
),
圆锥有(
)条高。
(2)
圆锥是由一个(
)面和一个(
)面组成的。圆锥的侧面展开图是个(
)形。
(3)
将右图中的直角三角形以长是6
cm的直角边所在直线为轴旋转一周,可以
得到一个(
),这个图形的高是(
)cm,底面直径是(
)cm。以长是5
cm的直角边所在直线为轴旋转一周,可以得到一个(
),这个图形的高
是(
)cm,底面直径是(
)cm。
圆
高
1
底
侧
扇
圆锥
6
10
圆锥
5
12
(4)
标出下面圆锥的顶点、高、底面半径。
顶点
高
底面半径
2.
下面的图形中,哪些是圆锥?
在下面的(
)里画“√”。
√
4.
转一转,体验一下会产生哪种立体图形,并用线连一连。
如图是一个棱长为10dm的正方体木块,要把它削成一个体积最大的圆锥,这个圆锥的高是多少分米?
底面半径是多少分米?
高:10dm
底面半径:10÷2=5(dm)
5.
如下图,在等腰三角形ABC中,AD=6
dm,BC=8
dm,以AD所在直线为轴旋转
180°。
(1)
可以得到一个什么立体图形?
(2)
这个立体图形的底面积是多少?高是多少?
圆锥
3.14×(8÷2)2=50.24(dm2) 高:6
dm
6.
一个圆锥的底面直径是18
cm,高是15
cm。如果将这个圆锥沿着高切成两半,
那么表面积将增加多少平方厘米?
15×18××2=270(cm2)
解析:把圆锥沿着高切成两半,增加的表面积就是两个三角形的面积,三角形的底是圆锥底面的直径,三角形的高是圆锥的高。
第8课时
圆锥的体积
1.
填空。
(1)
一个圆柱和一个圆锥等底等高,若圆锥的体积是24
cm3,则圆柱的体积是
(
);若圆柱的体积是24
cm3,则圆锥的体积是(
)。
(2)
把一个体积是270
dm3的圆柱形木料削成一个最大的圆锥,圆锥的体积是
(
),削去的体积是(
)。
(3)
一个圆锥,底面积是12
cm2,高是5
cm,体积是(
)。
(4)
一个圆锥和一个圆柱等底等高,体积相差40
cm3,圆柱的体积是(
),
圆锥的体积是(
)。
72
cm3
8
cm3
90
dm3
180
dm3
20
cm3
60
cm3
20
cm3
2.
判断。
(1)
圆柱的体积是圆锥体积的3倍。(?
)
(2)
等底等高的圆柱和圆锥,如果圆柱的体积是36
cm3,那么圆锥的体积是12
cm3。(?
)
(3)
一个圆锥的底面半径扩大为原来的3倍,高不变,它的体积就扩大为原来的3
倍。(
?)
3.计算下面各圆锥的体积。(单位:cm)
(1)
(2)
×
√
×
×3.14×(6÷2)2×5=47.1(cm3)
×3.14×22×9=37.68(cm3)
4.
一个圆锥形煤堆,底面直径是4
m,高是2.4
m。如果每立方米的煤约重1.4
t,
那么这个圆锥形煤堆大约重多少吨?(得数保留整数)
5.
一个圆锥形零件,它的体积是47.1
cm3,底面直径是6
cm。这个零件的高是多少?
6.
一个圆锥形粮堆,底面周长是6.28
m,高是1.8
m,把它放在一个底面积是6.28
m2的圆柱形粮囤里,可以堆多高?
×3.14×(4÷2)2×2.4=10.048(m3) 10.048×1.4≈14(t)
47.1÷÷[3.14×(6÷2)2]=5(cm)
6.28÷3.14÷2=1(m) ×3.14×12×1.8=1.884(m3) 1.884÷6.28=0.3(m)
7.
如下图,一个直角梯形绕较长底边旋转一周后形成的立体图形的体积是多少?
3.14×52×6+×3.14×52×(9-6)=549.5(cm3)
解析:把一个直角梯形绕较长底边旋转一周后形成的立体图形的体积等于一个圆柱的体积加一个圆锥的体积。
第9课时
练
习
课
1.
选择。
(1)
一个圆柱和一个圆锥等底等高,它们的体积之和是36
cm3,圆锥的体积是
(
)cm3。
①
12
②
9
③
18
(2)
将24个相同的铁圆锥熔铸成和它们等底等高的铁圆柱,得到的铁圆柱的数
量是(
)。
①
12个
②
8个
③
72个
(3)
把一个圆柱削成一个最大的圆锥,削去的体积是18
cm3,圆锥的体积是
(
)cm3。
①
27
②
6
③
9
②
②
③
(4)
一个圆柱和一个圆锥的体积和底面积分别相等,圆锥的高是12
dm,圆柱的
高是(
)。
①
12
dm
②
4
dm
③
36
dm
2.
求下面各圆锥的体积。
(1)
底面直径是12
cm,高是直径的。
(2)
底面周长是12.56
cm,高是2.7
cm。
3.
如下图,有一根底面直径是6
cm、长是15
cm的圆柱形钢材,把它削成与它等底
等高的圆锥形零件,要削去多少立方厘米的钢材?
②
×3.14×(12÷2)2×(12)=301.44(cm3)
×3.14×(12.56÷3.14÷2)2×2.7=11.304(cm3)
3.14×(6÷2)2×15×(1)=282.6(cm3)
4.
一块麦田收获的小麦,堆成了圆锥形。经测量,底面周长是5.652
m,高是1.5
m。
(1)
这堆小麦的体积是多少立方米?
(2)
如果每立方米小麦重0.7
t,那么这堆小麦有多重?(得数保留一位小数)
(3)
这块麦田有0.05公顷,根据(2)所得结果,平均每公顷收获小麦多少吨?
(4)
每吨小麦的售价是3200元,根据(2)所得结果,这些小麦全部售出能卖多少元?
5.
把一个底面积是3.14
cm2、高是9
cm的圆柱形零件铸造成一个底面积是18.84
cm2
的圆锥形零件。这个圆锥形零件的高是多少厘米?
×3.14×(5.652÷3.14÷2)2×1.5=1.2717(m3)
1.2717×0.7≈0.9(t)
0.9÷0.05=18(t)
0.9×3200=2880(元)
3.14×9÷÷18.84=4.5(cm)
6.
如下图,一个直角三角形的两条直角边分别是6
cm和8
cm,以直角三角形的一
条直角边为轴旋转一周,得到一个立体图形。求这个立体图形的体积。
以6
cm的直角边所在直线为轴旋转一周所得立体图形的体积:
×3.14×82×6=401.92(cm3)
以8
cm的直角边所在直线为轴旋转一周所得立体图形的体积:
×3.14×62×8=301.44(cm3)
解析:有两种情况,以6
cm的直角边所在直线为轴旋转一周,得到一个r=8
cm、h=6
cm的圆锥;以8
cm的直角边所在直线为轴旋转一周,得到一个r=6
cm、
h=8
cm的圆锥。
第10课时
整理与复习
1.
填表。
图形
半 径
直 径
高
表面积
体 积
圆柱
8
dm?
?4
dm
2
m
1.5m
0.4
cm
2.512
cm3
圆锥
6
dm
2.7
dm
/
0.8
cm
1.5
cm
/
2.
判断下面的圆锥与哪个圆柱的体积相等,在那个圆柱下面的( )里画“√”。(单位:cm)
?4
dm
200.96
dm2
200.96
dm3
1
m
15.7
m2
4.71
m3
0.8
cm
5
cm
13.5648
cm2
3
dm
1.6
cm
25.434
dm3
1.0048
cm3
√
3.
如下图是一个用塑料薄膜覆盖的蔬菜大棚,长为
15
m,横截面是一个直径为2
m的半圆。
(1)
这个蔬菜大棚的种植面积是多少平方米?
(2)
覆盖在这个蔬菜大棚上的塑料薄膜大约有多少平方米?
(3)
这个蔬菜大棚内的空间有多大?
15×2=30(m2)
3.14×2×15×+3.14×(2÷2)2÷2×2=50.24(m2)
3.14×(2÷2)2×15×=23.55(m3)
4.
一个圆锥形沙堆,它的底面周长是12.56
m,高是1.8
m。用这些沙在8
m宽的
公路上铺3
cm厚的路面,能铺多少米?
5.
一支圆柱形牙膏的管口直径是4
mm,张阿姨每天刷牙2次,每次挤出10
mm,这
支牙膏可以用36天。如果张阿姨每次挤出15
mm,那么这支牙膏可以用多少天?
6.
周阳生病了,医生给他输一瓶100
mL的药液,每分钟输2.5
mL。12
min后吊瓶
数据如下图,整个吊瓶的容积是多少?
×3.14×(12.56÷3.14÷2)2×1.8=7.536(m3)
3
cm=0.03
m 8×0.03=0.24(m2) 7.536÷0.24=31.4(m)
3.14×(4÷2)2×10×2×36=9043.2(mm3)
3.14×(4÷2)2×15×2=376.8(mm3) 9043.2÷376.8=24(天)
100-2.5×12+80=150(mL)
7.
如下图,张师傅用这张长方形铁皮的阴影部分,刚好围成一个圆柱形有盖水桶。
你能求出这个水桶的容积吗?(不计铁皮厚度)
3.14×(4÷2)2=12.56(dm2)
12.56×(4×2)=100.48(dm3)
100.48
dm3=100.48
L 解析:由题图可知,铁皮的左边两个圆做圆柱形水桶的两个底,右边的长方形铁皮做圆柱形水桶的侧面。
3
圆柱和圆锥
第1课时 圆柱的认识
1.
下面的图形中,哪些是圆柱?在下面的( )里画“
√
”。
√
√
2.
标出下面圆柱的高、底面、侧面。
3.
填空。
(1)
用一张长31.4
cm、宽15.7
cm的长方形厚纸板围成圆柱,有(
)种围法。
其中一种圆柱的高是(
)cm,底面直径是(
)cm;另一种圆柱的高是
(
)cm,底面直径是(
)cm。
(2)
把圆柱的侧面展开得到一个(
),这个(
)的长等于
圆柱的(
),宽等于圆柱的(
)。
(3)
当圆柱的(
)和(
)相等时,它的侧面沿高展开后是一个正
方形。
(4)
圆柱有(
)条高。
略
两
31.4
5
15.7
10
长方形
长方形
底面周长
高
高
底面周长
无数
4.
折一折,想一想,连一连。
5.
下面的图形(
)是圆柱的展开图。(单位:cm)
6.
一个圆柱形包装盒的侧面贴着一张商标纸,圆柱的高是16
cm,底面半径是5
cm。
这张商标纸展开后是一个长方形,它的长和宽各是多少厘米?
7.
如下图,一个圆柱的底面周长是9.42
cm,高是
5
cm,沿底面直径把它切成两
个半圆柱,一个半圆柱截面的面积是多少平方厘米?
②
长:2×3.14×5=31.4(cm) 宽:16
cm
9.42÷3.14×5=15(cm2)
8.
奶奶过生日,妈妈买了一个大蛋糕。蛋糕盒是圆柱形的,妈妈准备缠上十字形
的丝带再打上蝴蝶结(如下图),4
m长的丝带够吗?(蝴蝶结需要8
dm)
5×4+3×4+8=40(dm) 40
dm=4
m 4
m长的丝带够
解析:要求需要的丝带的长度,即是求缠十字形需要的丝带长度加上蝴蝶结的长度,缠十字形需要的丝带长度是4个底面直径与4个高的长度和。
第2课时
圆柱的表面积
1.
填空。
(1)
圆柱的表面积=(
)+(
)×2
圆柱的侧面积=(
)×(
)
(2)
一个圆柱的侧面积是50.24
dm2,高是4
dm,它的底面周长是(
)dm,
直径是(
)dm,底面积是(
)dm2。
(3)
一个圆柱的底面直径是6
cm,高是8
cm,它的侧面积是(
)cm2,
表面积是(
)cm2。
2.
计算下面各圆柱的底面积和侧面积。
(1)
底面半径是0.4
m,高是5
m。
圆柱的侧面积
底面积
底面周长
高
12.56
4
12.56
150.72
207.24
底面积:3.14×0.42=0.5024(m2) 侧面积:2×3.14×0.4×5=12.56(m2)
(2)
底面周长是18.84
cm,高是4
cm。
3.
求下面各圆柱的表面积。
(1)
(2)
(1)
3.14×(2÷2)2×2+3.14×2×3=25.12(dm2)
(2)
3.14×42×2+2×3.14×4×9=326.56(cm2)
底面积:3.14×(18.84÷3.14÷2)2=28.26(cm2)
侧面积:18.84×4=75.36(cm2)
4.
某建筑的中央有4根同样大小的圆柱形龙柱,它的高是19.2
m,底面直径是
1.2
m。如果在每根龙柱的表面刷一层油漆,那么刷油漆部分的面积是多少平
方米?(提示:只刷龙柱的侧面)
5.
一台压路机的滚筒宽1.5
m,直径是1
m。如果它每分钟滚动10周,那么滚动1
分钟,压过的面积是多少平方米?
3.14×1.2×19.2×4=289.3824(m2)
3.14×1×1.5×10=47.1(m2)
6.
一种圆柱形饮料瓶的底面周长是18.84
cm,高是10
cm,饮料的包装纸箱如下图,
你能算出这个纸箱的容积吗?
18.84÷3.14=6(cm) (6×6)×(6×4)×10=8640(cm3)
7.
一根圆柱形的小棒,底面直径是2
cm,高是15
cm。
(1)
把它沿着底面直径切成两个半圆柱,它的表面积增加了多少?
(2)
如果把它从正中间横切成两个相同的小圆柱,那么它的表面积增加了多少?
2×15×2=60(cm2)
解析:求增加的表面积就是求切开后两个半圆柱截面(长方形)的面积。
3.14×(2÷2)2×2=6.28(cm2)
解析:求增加的表面积就是求两个小圆柱的底面积。
第3课时
练
习
课
1.
下面的问题实际求的是什么?把问题前的字母填在相应的( )里。
A.
做圆柱形通风管需要的铁皮
B.
圆柱形水池的占地面积
C.
压路机滚筒转动一周压路的面积
D.
做有盖的圆柱形油桶需要的铁皮
E.
做圆柱形笔筒需要的纸板
(1)
求侧面积。(
)
(2)
求底面积。(
)
(3)
求表面积。(
)
(4)
求一个底面积与侧面积的和。(
)
A,C
B
D
E
2.
填空。
(1)
一个圆柱的底面半径为5
cm,高为15
cm,从中间横切成两个大小一样的小
圆柱,表面积增加了(
)cm2。
(2)
图形名称
已知条件
表面积
长方体
长8
m,宽5
m,高6.4
m
正方体
棱长4
cm
圆 柱
底面半径1.5
cm,高7
cm
?
底面周长31.4
dm,高10
dm
?
157
246.4
m2
96
cm2
80.07
cm2
471
dm2
3.
选择。
(1)
甲、乙两人用不同的方法分别将一张长20
cm、宽15
cm的纸围成一个圆柱
(接头处不重叠),则围成的圆柱的(
)。
①
高相等
②
侧面积相等
③
侧面积和高都相等
④
侧面积和高都不相等
(2)
有一个圆柱,按如下图所示的方式截成3段,增加了(
)个底面。
①
2
②
3
③
4
(3)
一个圆柱的高是25.12
cm,它的侧面展开图是一个正方形,它的底面半径
是(
)cm。
①
25.12
②
8
③
4
④
16
②
③
③
4.
有一个圆柱形蓄水池,底面半径为2
m,深3
m。在池底和池壁抹上水泥,如果
每平方米用水泥20
kg,那么一共要用水泥多少千克?
5.
计算下面图形的表面积。
6.
有一根圆柱形木棒,准备将它的表面刷上油漆。如果1
g油漆能刷5
cm2,那么
当这根木棒的底面半径为3
cm,长为2
m时,需要油漆多少克?
2×3.14×2×3+3.14×22=50.24(m2) 20×50.24=1004.8(kg)
3.14×2×10+(5×8+2×8+2×5)×2=194.8(dm2)
2
m=200
cm 2×3.14×3×200+3.14×32×2=3824.52(cm2)
3824.52÷5=764.904(g)
7.
如下图,把一根长60
cm的圆柱形木料截去10
cm长的一段,表面积就减少了
502.4
cm2。原来这根圆柱形木料的表面积是多少平方厘米?
直径:502.4÷10÷3.14=16(cm)
表面积:3.14×(16÷2)2×2+502.4×(60÷10)=3416.32(cm2)
解析:底面积没变,减少的502.4
cm2就是侧面积减少的部分,即可求出这根木料的底面直径,从而求出它的底面积,侧面积是减少的侧面积的(60÷10)倍。
第4课时
圆柱的体积
1.
填空。
(1)
如下图,把圆柱的底面分成许多个相等的扇形,然后把圆
柱切开,可以拼成一个近似的(
)体,这个(
)体的
底面积等于圆柱的(
),高等于圆柱的(
),长方体的体积等于
(
)乘(
),所以圆柱的体积的计算公式是(
)。
(2)
一个圆柱的底面半径是4
dm,高是4
dm,这个圆柱的体积是(
)dm3。
(3)
若圆柱的底面积扩大为原来的4倍,高扩大为原来的2倍,则体积扩大为原
来的(
)倍。
(4)
长方体、正方体和圆柱的体积都可以用(
)来计算。
(5)
7.5
dm3=(
)L=(
)mL
230
cm3=(
)mL=(
)L
长方
长方
底面积
高
底面积
高
圆柱的体积=底面积×高
200.96
8
体积=底面积×高
7.5
7500
230
0.23
2.
看图计算下面圆柱的体积。
(1)
(2)
3.
两个底面积相等的圆柱,一个圆柱的高是7
dm,体积是63
dm3;另一个圆柱的
高是5
dm,它的体积是多少立方分米?
3.14×(20÷2)2×40=12560(cm3)
5×18=90(cm3)
63÷7×5=45(dm3)
4.
一个圆柱形电饭煲,从里面量得底面周长是9.42
dm,高是2.8
dm。这个电饭
煲的容积大约是多少升?(得数保留整数)
5.
一辆油罐车的油罐是圆柱形的,底面直径是3
m,长是5
m。如果每立方米可装
汽油0.8
t,那么这辆油罐车最多可装汽油多少吨?
6.
如下图,这个杯子能装下这盒牛奶吗?(不计杯壁的厚度)(单位:cm)
3.14×(9.42÷3.14÷2)2×2.8=19.782(dm3)
19.782
dm3≈20
L
3.14×(3÷2)2×5×0.8=28.26(t)
3.14×(6÷2)2×8=226.08(cm3)
226.08
cm3=226.08
mL
因为226.08>225,所以这个杯子能装下这盒牛奶
7.
把一根长1.5
m的圆柱形钢材截成3段后如下图所示,表面积比原来增加9.6
dm2。
这根钢材原来的体积是多少立方分米?
1.5
m=15
dm 9.6÷[(3-1)×2]×15=36(dm3)
解析:解题的关键是求出这根钢材的底面积,钢材的底面积=增加的表面积÷增加的底面个数。
第5课时
解决实际问题
1.
填空。
(1)
我们常常利用(
)的特性,把不规则图形转化成(
)
来计算。
(2)
右图中,将图①的瓶子倒置变成图②,瓶子中水的体积不变,所以图①和图
②空置部分的体积(
)。由此可以将图①的空置部分转化成一个高是
(
)cm的圆柱形。要求瓶子的容积可以先根据图①求出(
)的体积,再根据图②
求出(
)的体积,两者相加就是瓶子的容积了。
(3)
把一个棱长为4分米的正方体木块削成一个最大的圆柱,这个圆柱的体积是
(
)立方分米。
(4)
加工厂将一块棱长为3
dm的正方体铁块熔铸成一个圆柱形零件,这个零件的
体积是(
)dm3。
体积不变
规则图形
相等
20
水
空置部分
50.24
27
2.
一个圆柱形粮囤,从里面量底面半径是3
m,高是2
m,这个粮囤最多能装粮多
少立方米?
3.
有一个长方体铁块的长是9
dm,宽是5
dm,高是3.14
dm。把它熔铸成一个底面
半径是3
dm的圆柱形铁块,这个圆柱形铁块的高是多少分米?
3.14×32×2=56.52(m3)
(9×5×3.14)÷(3.14×32)=5(dm)
4.
一个瓶子的高度是30
cm,底面内直径是8
cm,瓶子里的水的高度是20
cm(如
图①)。把瓶子倒置,这时水的高度是24
cm(如图②)。这个瓶子的容积是多少?
5.
一个水龙头的内直径是1.6
cm,打开水龙头后水的流速是30
cm/s。一个容积
是5
L的水桶,80
s能装满水吗?
6.
一个圆柱形水槽里面盛有10
cm深的水,水槽的底面积为200
cm2。现将一个棱
长为5
cm的正方体铁块放入水中(铁块完全浸没水中),水面将上升至多少厘米?
3.14×(8÷2)2×(30-24+20)=1306.24(cm3)
1306.24
cm3=1306.24
mL
3.14×(1.6÷2)2×30×80=4823.04(cm3) 4823.04
cm3=4.82304
L 因为4.82304<5,所以80
s不能装满水
5×5×5÷200+10=10.625(cm)
7.
如下图是一根底面直径是6
cm的圆柱形木料被斜着截去一段后剩下的部分。求
剩下的部分的体积。
3.14×(6÷2)2×(8+10)÷2=254.34(cm3)
解析:解答本题的关键是理解剩下的部分的体积是底面直径为6
cm、高为(8+10)cm的圆柱形体积的一半。
第6课时
练
习
课
1.
选择。
(1)
圆柱的高不变,若底面半径扩大为原来的3倍,则体积应该(
)。
①
扩大为原来的3倍
②
扩大为原来的6倍
③
扩大为原来的9倍
④
不变
(2)
等底等高的圆柱、正方体、长方体的体积相比较,(
)。
①
正方体的体积大
②
长方体的体积大
③
一样大
(3)
有甲、乙两个等底的圆柱,如果甲圆柱的高是乙圆柱高的,那么甲圆柱的
体积是乙圆柱体积的(
)。
①
②
③
(4)
求一个圆柱形水桶能盛多少水,就是求水桶的(
)。
①
表面积
②
体积
③
容积
③
③
②
③
2.
填表。
底面半径/m
底面直径/m
高/m
圆柱的表面积/m2
圆柱的体积/m3
10
6
14
5
3
141.3
3.
如下图,这根钢管长50
m,每立方厘米的钢管重
8
g,这根钢管重多少千克?
7
20
6
5
1004.8
527.52
150.72
1884
769.3
50
m=5000
cm 3.14××5000×8=879200(g)
879200
g=879.2
kg
4.
赵雪家有15个底面积是40
cm2、高是10
cm的圆柱形水杯,一壶水正好能倒满3
杯。如果让12位客人都能喝上这壶水,那么平均每杯倒多少毫升?
5.
一根圆柱形水管,内直径是20
cm,水流的速度是5
m/s。这根水管每分钟最多
流过多少立方米的水?
6.
有一张长方形的纸,长是24
cm,宽是12
cm,分别以它的长和宽所在直线为轴
旋转一周,得到两个圆柱体,它们的体积差是多少?
40×10×3÷12=100(cm3) 100
cm3=100
mL
20
cm=0.2
m 3.14×(0.2÷2)2×5×60=9.42(m3)
3.14×242×12-3.14×122×24=10851.84(cm3)
7.
下面4个图形的面积都是100
cm2,用这些图形分别卷成圆柱,哪个圆柱的体积
最大?哪个圆柱的体积最小?你有什么发现?(单位:cm,圆柱的底面周长等于
长方形的长,得数保留整数)
图形①:3.14×(50÷3.14÷2)2×2≈398(cm3)
图形②:3.14×(25÷3.14÷2)2×4≈199(cm3)
图形③:3.14×(20÷3.14÷2)2×5≈159(cm3)
图形④:3.14×(10÷3.14÷2)2×10≈80(cm3)
因为80<159<199<398,所以图形①卷成的圆柱的体积最大,图形④卷成的圆柱的体积最小 发现:面积相等的长方形或正方形,以长方形的长为圆柱的底面周长,长方形的长和宽的差距越大,卷成的圆柱的体积则越大;长方形的长和宽的差距越小,卷成的圆柱的体积则越小(合理即可) 解析:分别求出4个图形卷成圆柱的底面半径,再分别求出它们的体积进行比较。
第7课时
圆锥的认识
1.
填空。
(1)
圆锥的底面是个(
),从圆锥的顶点到底面圆心的距离是圆锥的(
),
圆锥有(
)条高。
(2)
圆锥是由一个(
)面和一个(
)面组成的。圆锥的侧面展开图是个(
)形。
(3)
将右图中的直角三角形以长是6
cm的直角边所在直线为轴旋转一周,可以
得到一个(
),这个图形的高是(
)cm,底面直径是(
)cm。以长是5
cm的直角边所在直线为轴旋转一周,可以得到一个(
),这个图形的高
是(
)cm,底面直径是(
)cm。
圆
高
1
底
侧
扇
圆锥
6
10
圆锥
5
12
(4)
标出下面圆锥的顶点、高、底面半径。
顶点
高
底面半径
2.
下面的图形中,哪些是圆锥?
在下面的(
)里画“√”。
√
4.
转一转,体验一下会产生哪种立体图形,并用线连一连。
如图是一个棱长为10dm的正方体木块,要把它削成一个体积最大的圆锥,这个圆锥的高是多少分米?
底面半径是多少分米?
高:10dm
底面半径:10÷2=5(dm)
5.
如下图,在等腰三角形ABC中,AD=6
dm,BC=8
dm,以AD所在直线为轴旋转
180°。
(1)
可以得到一个什么立体图形?
(2)
这个立体图形的底面积是多少?高是多少?
圆锥
3.14×(8÷2)2=50.24(dm2) 高:6
dm
6.
一个圆锥的底面直径是18
cm,高是15
cm。如果将这个圆锥沿着高切成两半,
那么表面积将增加多少平方厘米?
15×18××2=270(cm2)
解析:把圆锥沿着高切成两半,增加的表面积就是两个三角形的面积,三角形的底是圆锥底面的直径,三角形的高是圆锥的高。
第8课时
圆锥的体积
1.
填空。
(1)
一个圆柱和一个圆锥等底等高,若圆锥的体积是24
cm3,则圆柱的体积是
(
);若圆柱的体积是24
cm3,则圆锥的体积是(
)。
(2)
把一个体积是270
dm3的圆柱形木料削成一个最大的圆锥,圆锥的体积是
(
),削去的体积是(
)。
(3)
一个圆锥,底面积是12
cm2,高是5
cm,体积是(
)。
(4)
一个圆锥和一个圆柱等底等高,体积相差40
cm3,圆柱的体积是(
),
圆锥的体积是(
)。
72
cm3
8
cm3
90
dm3
180
dm3
20
cm3
60
cm3
20
cm3
2.
判断。
(1)
圆柱的体积是圆锥体积的3倍。(?
)
(2)
等底等高的圆柱和圆锥,如果圆柱的体积是36
cm3,那么圆锥的体积是12
cm3。(?
)
(3)
一个圆锥的底面半径扩大为原来的3倍,高不变,它的体积就扩大为原来的3
倍。(
?)
3.计算下面各圆锥的体积。(单位:cm)
(1)
(2)
×
√
×
×3.14×(6÷2)2×5=47.1(cm3)
×3.14×22×9=37.68(cm3)
4.
一个圆锥形煤堆,底面直径是4
m,高是2.4
m。如果每立方米的煤约重1.4
t,
那么这个圆锥形煤堆大约重多少吨?(得数保留整数)
5.
一个圆锥形零件,它的体积是47.1
cm3,底面直径是6
cm。这个零件的高是多少?
6.
一个圆锥形粮堆,底面周长是6.28
m,高是1.8
m,把它放在一个底面积是6.28
m2的圆柱形粮囤里,可以堆多高?
×3.14×(4÷2)2×2.4=10.048(m3) 10.048×1.4≈14(t)
47.1÷÷[3.14×(6÷2)2]=5(cm)
6.28÷3.14÷2=1(m) ×3.14×12×1.8=1.884(m3) 1.884÷6.28=0.3(m)
7.
如下图,一个直角梯形绕较长底边旋转一周后形成的立体图形的体积是多少?
3.14×52×6+×3.14×52×(9-6)=549.5(cm3)
解析:把一个直角梯形绕较长底边旋转一周后形成的立体图形的体积等于一个圆柱的体积加一个圆锥的体积。
第9课时
练
习
课
1.
选择。
(1)
一个圆柱和一个圆锥等底等高,它们的体积之和是36
cm3,圆锥的体积是
(
)cm3。
①
12
②
9
③
18
(2)
将24个相同的铁圆锥熔铸成和它们等底等高的铁圆柱,得到的铁圆柱的数
量是(
)。
①
12个
②
8个
③
72个
(3)
把一个圆柱削成一个最大的圆锥,削去的体积是18
cm3,圆锥的体积是
(
)cm3。
①
27
②
6
③
9
②
②
③
(4)
一个圆柱和一个圆锥的体积和底面积分别相等,圆锥的高是12
dm,圆柱的
高是(
)。
①
12
dm
②
4
dm
③
36
dm
2.
求下面各圆锥的体积。
(1)
底面直径是12
cm,高是直径的。
(2)
底面周长是12.56
cm,高是2.7
cm。
3.
如下图,有一根底面直径是6
cm、长是15
cm的圆柱形钢材,把它削成与它等底
等高的圆锥形零件,要削去多少立方厘米的钢材?
②
×3.14×(12÷2)2×(12)=301.44(cm3)
×3.14×(12.56÷3.14÷2)2×2.7=11.304(cm3)
3.14×(6÷2)2×15×(1)=282.6(cm3)
4.
一块麦田收获的小麦,堆成了圆锥形。经测量,底面周长是5.652
m,高是1.5
m。
(1)
这堆小麦的体积是多少立方米?
(2)
如果每立方米小麦重0.7
t,那么这堆小麦有多重?(得数保留一位小数)
(3)
这块麦田有0.05公顷,根据(2)所得结果,平均每公顷收获小麦多少吨?
(4)
每吨小麦的售价是3200元,根据(2)所得结果,这些小麦全部售出能卖多少元?
5.
把一个底面积是3.14
cm2、高是9
cm的圆柱形零件铸造成一个底面积是18.84
cm2
的圆锥形零件。这个圆锥形零件的高是多少厘米?
×3.14×(5.652÷3.14÷2)2×1.5=1.2717(m3)
1.2717×0.7≈0.9(t)
0.9÷0.05=18(t)
0.9×3200=2880(元)
3.14×9÷÷18.84=4.5(cm)
6.
如下图,一个直角三角形的两条直角边分别是6
cm和8
cm,以直角三角形的一
条直角边为轴旋转一周,得到一个立体图形。求这个立体图形的体积。
以6
cm的直角边所在直线为轴旋转一周所得立体图形的体积:
×3.14×82×6=401.92(cm3)
以8
cm的直角边所在直线为轴旋转一周所得立体图形的体积:
×3.14×62×8=301.44(cm3)
解析:有两种情况,以6
cm的直角边所在直线为轴旋转一周,得到一个r=8
cm、h=6
cm的圆锥;以8
cm的直角边所在直线为轴旋转一周,得到一个r=6
cm、
h=8
cm的圆锥。
第10课时
整理与复习
1.
填表。
图形
半 径
直 径
高
表面积
体 积
圆柱
8
dm?
?4
dm
2
m
1.5m
0.4
cm
2.512
cm3
圆锥
6
dm
2.7
dm
/
0.8
cm
1.5
cm
/
2.
判断下面的圆锥与哪个圆柱的体积相等,在那个圆柱下面的( )里画“√”。(单位:cm)
?4
dm
200.96
dm2
200.96
dm3
1
m
15.7
m2
4.71
m3
0.8
cm
5
cm
13.5648
cm2
3
dm
1.6
cm
25.434
dm3
1.0048
cm3
√
3.
如下图是一个用塑料薄膜覆盖的蔬菜大棚,长为
15
m,横截面是一个直径为2
m的半圆。
(1)
这个蔬菜大棚的种植面积是多少平方米?
(2)
覆盖在这个蔬菜大棚上的塑料薄膜大约有多少平方米?
(3)
这个蔬菜大棚内的空间有多大?
15×2=30(m2)
3.14×2×15×+3.14×(2÷2)2÷2×2=50.24(m2)
3.14×(2÷2)2×15×=23.55(m3)
4.
一个圆锥形沙堆,它的底面周长是12.56
m,高是1.8
m。用这些沙在8
m宽的
公路上铺3
cm厚的路面,能铺多少米?
5.
一支圆柱形牙膏的管口直径是4
mm,张阿姨每天刷牙2次,每次挤出10
mm,这
支牙膏可以用36天。如果张阿姨每次挤出15
mm,那么这支牙膏可以用多少天?
6.
周阳生病了,医生给他输一瓶100
mL的药液,每分钟输2.5
mL。12
min后吊瓶
数据如下图,整个吊瓶的容积是多少?
×3.14×(12.56÷3.14÷2)2×1.8=7.536(m3)
3
cm=0.03
m 8×0.03=0.24(m2) 7.536÷0.24=31.4(m)
3.14×(4÷2)2×10×2×36=9043.2(mm3)
3.14×(4÷2)2×15×2=376.8(mm3) 9043.2÷376.8=24(天)
100-2.5×12+80=150(mL)
7.
如下图,张师傅用这张长方形铁皮的阴影部分,刚好围成一个圆柱形有盖水桶。
你能求出这个水桶的容积吗?(不计铁皮厚度)
3.14×(4÷2)2=12.56(dm2)
12.56×(4×2)=100.48(dm3)
100.48
dm3=100.48
L 解析:由题图可知,铁皮的左边两个圆做圆柱形水桶的两个底,右边的长方形铁皮做圆柱形水桶的侧面。
