五年级下册数学习题课件-2 因数与倍数 人教版(共29张PPT)
文档属性
| 名称 | 五年级下册数学习题课件-2 因数与倍数 人教版(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
2 因数与倍数
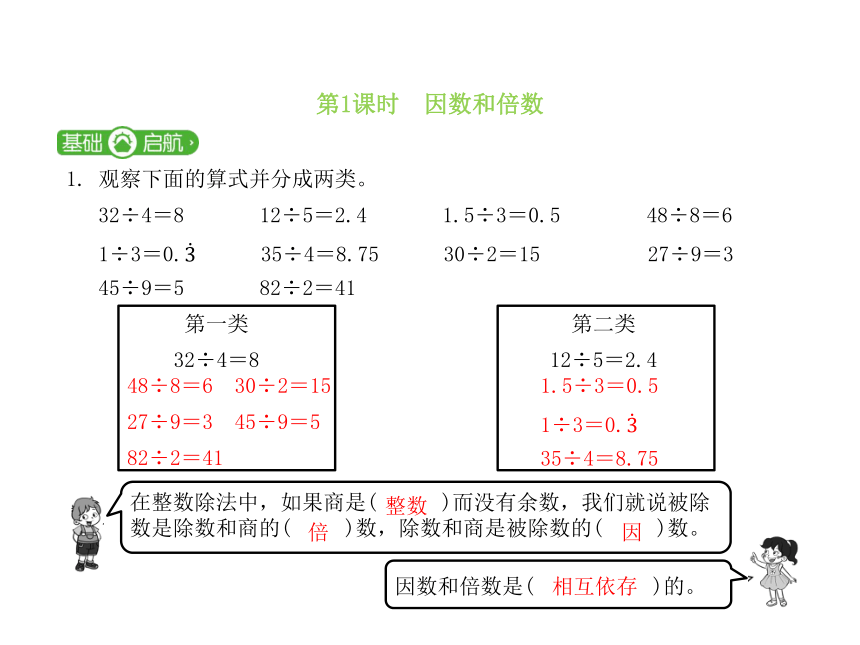
第1课时 因数和倍数
1.
观察下面的算式并分成两类。
32÷4=8
12÷5=2.4
1.5÷3=0.5
48÷8=6
1÷3=0.
35÷4=8.75
30÷2=15
27÷9=3
45÷9=5
82÷2=41
第一类
第二类
32÷4=8
12÷5=2.4
48÷8=6
30÷2=15
27÷9=3
45÷9=5
82÷2=41
1.5÷3=0.5
1÷3=0.
35÷4=8.75
在整数除法中,如果商是(
)而没有余数,我们就说被除数是除数和商的(
)数,除数和商是被除数的(
)数。
因数和倍数是(
)的。
整数
倍
因
相互依存
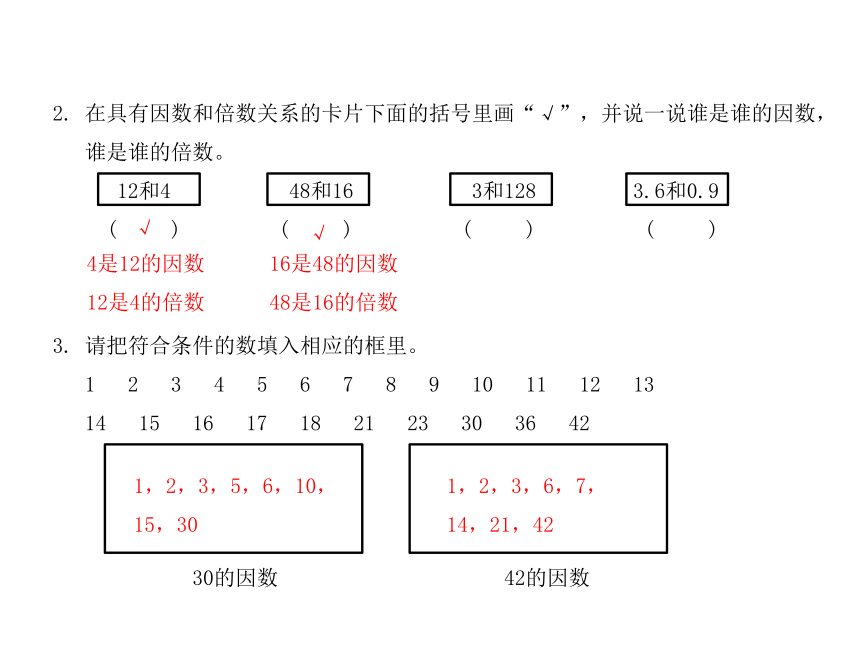
2.
在具有因数和倍数关系的卡片下面的括号里画“√”,并说一说谁是谁的因数,
谁是谁的倍数。
12和4
48和16
3和128
3.6和0.9
(
)
(
)
(
)
(
)
3.
请把符合条件的数填入相应的框里。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
21
23
30
36
42
30的因数
42的因数
4是12的因数
12是4的倍数
16是48的因数
48是16的倍数
1,2,3,5,6,10,15,30
1,2,3,6,7,14,21,42
√
√
4.
(1)
写出下面各数的因数。
8的因数
19的因数
18的因数
25的因数
(2)
写出下面各数的倍数。(各写5个)
3的倍数
7的倍数
2的倍数
13的倍数
1,2,4,8
1,19
1,2,3,6,9,18
1,5,25
3,6,9,12,15
7,14,21,28,35
2,4,6,8,10
13,26,39,52,64
答案不唯一
5.
涂一涂。
6.
五(1)班有36名同学,体育课上同学们面向老师站成一排,从左到右报数:1,
2,3,4,…,35,36。老师让所报的数是3的倍数的同学向后转,接着又让所
报的数是5的倍数的同学向后转,现在面向老师的同学有多少名?
19名 解析:一共有的同学(36名)-报数是3的倍数的同学(12名)-报数是5的倍数的同学(7名)+重复的同学(2名),即可求解。
第2课时 练
习
课
1.
判一判。
(1)
因为28÷4=7,所以28是倍数,4和7是因数。
(
)
(2)
5的倍数的个数比50000的因数的个数少。
(
)
(3)
10的因数有4个。
(
)
(4)
一个数的因数一定小于它的倍数。
(
)
(5)
任何数都没有最大的因数。
(
)
2.
填一填。
(1)
50以内7的倍数有(
)。
(2)
一个数的因数的个数是(
)的,其中最小因数是(
),最大因
数是(
)。
(3)
一个数的倍数的个数是(
)的,其中最小倍数是(
)。
×
×
√
×
×
7,14,21,28,35,42,49
有限
1
它本身
无限
它本身
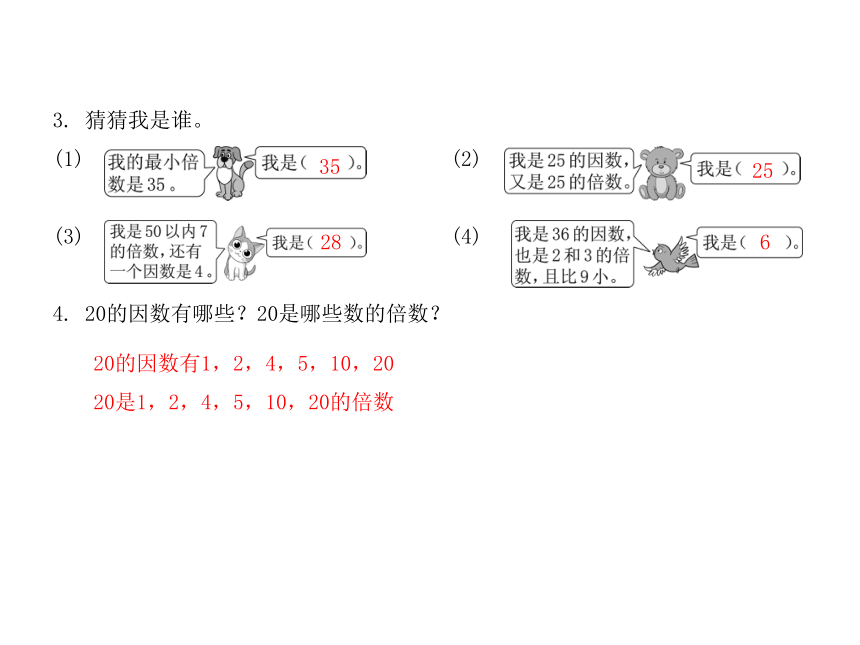
3.
猜猜我是谁。
(1)
(2)
(3)
(4)
4.
20的因数有哪些?20是哪些数的倍数?
20的因数有1,2,4,5,10,20
20是1,2,4,5,10,20的倍数
35
25
28
6
(2)
一个数是48的因数,同时也是3的倍数,这个数可能是多少?
(3)
一个两位数是5的倍数,同时也有因数4,这个数可能是多少?
6.
想一想,填一填,你发现了什么?
(1)
35是7的倍数,14也是7的倍数,35和14的和是7的倍数吗?
(
),我发现:(
)。
(2)
45是5的倍数,25也是5的倍数,45和25的差是5的倍数吗?
(
),我发现:(
)。
举例不唯一,如70是10的倍数,50是10的倍数,70和50的和是10的倍数,70和50的差也是10的倍数
可能是3,6,12,24,48
可能是20,40,60,80
是
两个数分别是同一个数的倍数,它们的和也是这个数的倍数
是
两个数分别是同一个数的倍数,它们的差也是这个数的倍数
5.
解决问题。
(1)
一个小于30的自然数,既是8的倍数,又是12的倍数,这个数是多少?
24
7.
欢欢和乐乐喜欢收集邮票,他们收集到的邮票枚数在100以内,并且比3和5的
倍数少2。欢欢和乐乐最多收集了多少枚邮票?
88枚 解析:100以内3和5的倍数最大是90,比90少2的是88,所以欢欢和乐乐最多收集了88枚邮票。
第3课时 2、5的倍数的特征
1.
我会填。
(1)
个位上是(
)的数,都是2的倍数;个位上是(
)或
(
)的数,都是5的倍数。
(2)
整数中,是2的倍数的数叫做(
),0也是(
)数;不是2的倍数
的数叫做(
)。
(3)
在36,21,40,70,75,130中,2的倍数有(
),5的倍
数有(
),既是2的倍数,又是5的倍数有(
)。
2.
将各队的球衣找出来,并将球衣号码填在各自的方框里。
0,2,4,6,8
0
5
偶数
偶
奇数
36,40,70,130
40,70,75,130
40,70,130
49,17,21,91,1
30,62,18,16,0
3.
把下面各数按要求填在横线上。
15
46
57
28
90
10
215
500
95
55
410
125
5的倍数:_______________________________________。
2的倍数:_______________________________________。
既是2的倍数,又是5的倍数:______________________。
我发现,既是2的倍数,又是5的倍数的数的特征:_________________。
4.
按要求在
里填数。
(1)
是5的倍数中最大的两位数。
(2)
两个数位上的数相同,且是最大的偶数。
(3)
54
既有因数2,又有因数5。
(4)
既是5的倍数,又是最小的三位奇数。
15,90,10,215,500,95,55,410,125
46,28,90,10,500,410
90,10,500,410
个位上都是0
9
5
8
8
0
1
0
5
5.
(1)
这样数数,数出来的数都是(
)的倍数,数到第(
)个数是一百三十。
(2)
这样数数,数出来的数都是(
)的倍数,第31个数是(
)。
6.
请用下面的数字卡片按要求写出两位数。
0 6 5 1
奇数:_____________________。
偶数:____________________。
5的倍数:__________________。
既是2的倍数,又是5的倍数:__________。
10或2或5
13
2
62
65,61,51,15
60,50,10,56,16
60,50,10,65,15
60,50,10
解析:在按要求写数的同时,注意排列组合的顺序,这样可以做到不重复、不遗漏。
第4课时 3的倍数的特征
1.
观察下面的数表,回答问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
……
(1)
下面是数表中的其中一排数,按照上面数表中的规律,在这排数中圈出相应的数。
51
52
53
54
55
56
57
58
59
60
(2)
我发现:一个数(
)上的数的和是3的倍数,这个数就是3的倍数。
(3)
根据发现,2017应该圈上吗?为什么?
不应该圈上 因为它不是3的倍数
各位
2.
不计算,把小白兔要采的蘑菇涂上你喜欢的颜色。
3.
不计算,你能很快说出哪几道算式的得数没有余数吗?在没有余数的算式
下面的
里画“√”。
√
√
√
4.
下面的数字卡片摆出的数中哪些是3的倍数?若是,则在后面的
里画“√”;
若不是,则在
里填一个数字,使这个三位数成为3的倍数。
5.
在
里填一个数字,使每个数都是3的倍数,各有几种填法?分别填在括号
里。
8
(
)
62
(
)
75
(
)
9
9(
)
4
18(
)
16
6(
)
6
3
2
8
5
6
7
5
2
7
9
3
1,4,7
1,4,7
0,3,6,9
0,3,6,9
2,5,8
2,5,8
√
2
或
5
或
8
1
或
4
或
7
√
√
√
6.
李老师买了124本笔记本,要平均分给五年级三个班,至少要再买几本才能正
好分完?
7.
按要求填数。
(1)
在下面的
里填一个数字,使这个数既是2的倍数,又是3的倍数。
?
5
73
194
(2)
在下面的
里填一个数字,使这个数既是3的倍数,又是5的倍数。
16
90
258
1+2+4=7 7+2=9 至少要再买2本才能正好分完
8.
在
中,
里最小填几,这个数就是3的倍数?最大呢?
最小填1,最大填7 解析:2017个8不能被3整除,但2016个8可以被3整除,多的1个8凑成3的倍数即可,所以可以加上1或4或7,最小为1,最大为7。
4
2
或
8
1
或
4
或
7
5
0
0
第5课时 练
习
课
1.
把下面各数填入相应的圈里。
6
9
7
10
13
14
17
18
50
69
20
75
30
123
2的倍数
3的倍数
5的倍数
同时是2,3,5的倍数的数是(
)。
2.
判一判。
(1)
同时是2,3,5的倍数的数一定是偶数。
(
)
(2)
3个连续自然数的和一定是3的倍数。
(
)
(3)
偶数一定比奇数大。
(
)
(4)
2的倍数是偶数,3的倍数是奇数。
(
)
6,10,14,18,50,20,30
6,9,18,69,75,30,123
10,50,20,75,30
30
√
√
×
×
3.
1+6=7 7+2=9 至少要添2个苹果才能正好分完
4.
为了表彰在“学雷锋”活动中涌现出来的先进个人,齐老师买了5个文具盒和
一些钢笔作为奖品。
售货员找给齐老师的钱对不对?请说明理由。
不对 理由:因为5个文具盒正好是40元,一些钢笔的钱数的个位上是0或5,所以齐老师实际需付出的总钱数的个位上一定是0或5。因此售货员找回的钱数的个位上也一定是0或5,而不应该是4。
5.
选出两个数字组成一个两位数,分别满足下面的条件。
(1)
3的倍数:__________________。
(2)
同时是2和3的倍数:________。
(3)
同时是3和5的倍数:________。
(4)
同时是2和5的倍数:______________。
78,87,75,57
78
75
70,80,50
6.
圈出下表中9的倍数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
(1)
9的倍数都是3的倍数吗?
(2)
只看个位,能否判断一个数是不是9的倍数?如果不能,那么应该怎样判断?
是
不能 一个数各位上数的和是9的倍数,这个数就是9的倍数
7.
有一把钥匙能同时开4把锁,请你根据下面的信息找到钥匙的密码。
这把钥匙的密码是(
)。
解析:3的倍数的两位数且小于32的有12,15,18,21,24,27,30,其中是奇数的有15,21,27,再根据所有因数的和是32,可得这把钥匙的密码是21。
21
第6课时 质数和合数
1.
填一填。
(1)
一个数,如果只有(
)和(
)两个因数,那么这样的数叫做质
数(或素数)。
(2)
一个数,如果除了(
)还有别的因数,那么这样的数叫做合数。
(3)
20以内的质数有(
),其中(
)是偶数。
2.
判一判。
(1)
自然数不是质数就是合数。
(
)
(2)
所有的奇数都是质数,所有的偶数都是合数。
(
)
(3)
任意两个自然数的积都是合数。
(
)
(4)
两个质数的积一定是合数。
(
)
(5)
合数只有3个因数。
(
)
(6)
在所有质数中,只有2是偶数,其余都是奇数。
(
)
1
它本身
1和它本身
2,3,5,7,11,13,17,19
2
×
×
×
√
×
√
3.
将下面各数分别填入指定的方框里。
1
27
41
56
61
63
84
85
11
15
30
49
2
73
91
98
奇数
偶数
质数
合数
4.
猜一猜。(在括号里填上合适的数)
(
)
(
)
(1)
1,27,41,61,63,85,11,15,49,73
91
56,84,30,2,98
41,61,11,2,73
27,56,63,84,85,15,30,49,91,98
5
7
(2)
(
)
(
)
(
)
(
)
(3)
5.
想一想,填一填。
(1)
质数:
3,
里可以填(
)。
4
,
里可以填(
)。
(2)
合数:
7,
里可以填(
)。
5
,
里可以填(
)。
97
4
8
10
1,2,4,5,7,8
1,3,7
2,5,7,8
0,1,2,4,5,6,7,8
6.
欢欢用一根长38
cm的铁丝围成一个长方形,这个长方形的长和宽都是质数。
38÷2=19(cm
) 19=17+2 17×2=34(cm2)
解析:用38
cm长的铁丝围成一个长方形,即这个长方形的周长是38
cm,先用38÷2=19(cm),算出一条长和一条宽的长度,再根据长和宽都是质数,可以推出19=17+2,即长方形的长和宽分别是17
cm和2
cm,最后用“长×宽”算出长方形的面积是17×2=34(cm2)。
第7课时 解决问题
1.
仔细观察,填一填。(填“奇”或“偶”)
46 16 24 2
10 74 8 98
5 11 1 29
9 37 37 85
(1)
①
左图中的数都是(
)数,任意两个数相加的和是(
)数。
②
右图中的数都是(
)数,任意两个数相加的和是(
)数。
③
从左图中任意挑出一个数与右图中任意一个数相加,和是(
)数。
奇
偶
偶
奇
偶
奇
偶
偶
(2)
①
左图中任意两个数相乘的积是(
)数。
②
右图中任意两个数相乘的积是(
)数。
③
从左图中任意挑出一个数与右图中任意一个数相乘,积是(
)数。
2.
不计算,直接判断结果是奇数还是偶数。
46+27(
)
34+108(
)
13×72(
)
268×54(
)
89+415(
)
71×67(
)
143+2(
)
212×71(
)
偶
奇
偶
奇
偶
偶
奇数
偶数
偶数
偶数
偶数
奇数
奇数
偶数
3.
探索15的倍数的特征。
准备:我先写出一组15的倍数:15,30,
______________________________________……
观察:这些数个位上的数字都是(
),每个数各位上的数的和都是
(
)的倍数。
发现:15的倍数的特征是个位上的数字是(
)或(
),且各位上的数的
和是(
)的倍数。
4.
有45个苹果要分装在甲、乙两个袋子里。如果甲袋装的个数是偶数,那么乙袋
装的个数是偶数还是奇数?如果甲袋装的个数是奇数呢?
?
如果甲袋装的个数是偶数,那么乙袋装的个数是奇数;如果甲袋装的个数是奇数,那么乙袋装的个数是偶数
答案不唯一,如45,60,75,90,105
0或5
3
0
5
3
5.
你知道“哥德巴赫猜想”吗?请根据该结论把下面的合数写成两个质数的和。
28=(
)+(
)
40=(
)+(
)
56=(
)+(
)
100=(
)+(
)
答案不唯一
6.
有24个苹果,把它们放在9个盘子里,每个盘子里只能放奇数个,这件事你
能办到吗?为什么?
办不到 因为9个奇数的和一定还是奇数,不可能是偶数
17
11
17
23
53
3
97
3
2 因数与倍数
第1课时 因数和倍数
1.
观察下面的算式并分成两类。
32÷4=8
12÷5=2.4
1.5÷3=0.5
48÷8=6
1÷3=0.
35÷4=8.75
30÷2=15
27÷9=3
45÷9=5
82÷2=41
第一类
第二类
32÷4=8
12÷5=2.4
48÷8=6
30÷2=15
27÷9=3
45÷9=5
82÷2=41
1.5÷3=0.5
1÷3=0.
35÷4=8.75
在整数除法中,如果商是(
)而没有余数,我们就说被除数是除数和商的(
)数,除数和商是被除数的(
)数。
因数和倍数是(
)的。
整数
倍
因
相互依存
2.
在具有因数和倍数关系的卡片下面的括号里画“√”,并说一说谁是谁的因数,
谁是谁的倍数。
12和4
48和16
3和128
3.6和0.9
(
)
(
)
(
)
(
)
3.
请把符合条件的数填入相应的框里。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
21
23
30
36
42
30的因数
42的因数
4是12的因数
12是4的倍数
16是48的因数
48是16的倍数
1,2,3,5,6,10,15,30
1,2,3,6,7,14,21,42
√
√
4.
(1)
写出下面各数的因数。
8的因数
19的因数
18的因数
25的因数
(2)
写出下面各数的倍数。(各写5个)
3的倍数
7的倍数
2的倍数
13的倍数
1,2,4,8
1,19
1,2,3,6,9,18
1,5,25
3,6,9,12,15
7,14,21,28,35
2,4,6,8,10
13,26,39,52,64
答案不唯一
5.
涂一涂。
6.
五(1)班有36名同学,体育课上同学们面向老师站成一排,从左到右报数:1,
2,3,4,…,35,36。老师让所报的数是3的倍数的同学向后转,接着又让所
报的数是5的倍数的同学向后转,现在面向老师的同学有多少名?
19名 解析:一共有的同学(36名)-报数是3的倍数的同学(12名)-报数是5的倍数的同学(7名)+重复的同学(2名),即可求解。
第2课时 练
习
课
1.
判一判。
(1)
因为28÷4=7,所以28是倍数,4和7是因数。
(
)
(2)
5的倍数的个数比50000的因数的个数少。
(
)
(3)
10的因数有4个。
(
)
(4)
一个数的因数一定小于它的倍数。
(
)
(5)
任何数都没有最大的因数。
(
)
2.
填一填。
(1)
50以内7的倍数有(
)。
(2)
一个数的因数的个数是(
)的,其中最小因数是(
),最大因
数是(
)。
(3)
一个数的倍数的个数是(
)的,其中最小倍数是(
)。
×
×
√
×
×
7,14,21,28,35,42,49
有限
1
它本身
无限
它本身
3.
猜猜我是谁。
(1)
(2)
(3)
(4)
4.
20的因数有哪些?20是哪些数的倍数?
20的因数有1,2,4,5,10,20
20是1,2,4,5,10,20的倍数
35
25
28
6
(2)
一个数是48的因数,同时也是3的倍数,这个数可能是多少?
(3)
一个两位数是5的倍数,同时也有因数4,这个数可能是多少?
6.
想一想,填一填,你发现了什么?
(1)
35是7的倍数,14也是7的倍数,35和14的和是7的倍数吗?
(
),我发现:(
)。
(2)
45是5的倍数,25也是5的倍数,45和25的差是5的倍数吗?
(
),我发现:(
)。
举例不唯一,如70是10的倍数,50是10的倍数,70和50的和是10的倍数,70和50的差也是10的倍数
可能是3,6,12,24,48
可能是20,40,60,80
是
两个数分别是同一个数的倍数,它们的和也是这个数的倍数
是
两个数分别是同一个数的倍数,它们的差也是这个数的倍数
5.
解决问题。
(1)
一个小于30的自然数,既是8的倍数,又是12的倍数,这个数是多少?
24
7.
欢欢和乐乐喜欢收集邮票,他们收集到的邮票枚数在100以内,并且比3和5的
倍数少2。欢欢和乐乐最多收集了多少枚邮票?
88枚 解析:100以内3和5的倍数最大是90,比90少2的是88,所以欢欢和乐乐最多收集了88枚邮票。
第3课时 2、5的倍数的特征
1.
我会填。
(1)
个位上是(
)的数,都是2的倍数;个位上是(
)或
(
)的数,都是5的倍数。
(2)
整数中,是2的倍数的数叫做(
),0也是(
)数;不是2的倍数
的数叫做(
)。
(3)
在36,21,40,70,75,130中,2的倍数有(
),5的倍
数有(
),既是2的倍数,又是5的倍数有(
)。
2.
将各队的球衣找出来,并将球衣号码填在各自的方框里。
0,2,4,6,8
0
5
偶数
偶
奇数
36,40,70,130
40,70,75,130
40,70,130
49,17,21,91,1
30,62,18,16,0
3.
把下面各数按要求填在横线上。
15
46
57
28
90
10
215
500
95
55
410
125
5的倍数:_______________________________________。
2的倍数:_______________________________________。
既是2的倍数,又是5的倍数:______________________。
我发现,既是2的倍数,又是5的倍数的数的特征:_________________。
4.
按要求在
里填数。
(1)
是5的倍数中最大的两位数。
(2)
两个数位上的数相同,且是最大的偶数。
(3)
54
既有因数2,又有因数5。
(4)
既是5的倍数,又是最小的三位奇数。
15,90,10,215,500,95,55,410,125
46,28,90,10,500,410
90,10,500,410
个位上都是0
9
5
8
8
0
1
0
5
5.
(1)
这样数数,数出来的数都是(
)的倍数,数到第(
)个数是一百三十。
(2)
这样数数,数出来的数都是(
)的倍数,第31个数是(
)。
6.
请用下面的数字卡片按要求写出两位数。
0 6 5 1
奇数:_____________________。
偶数:____________________。
5的倍数:__________________。
既是2的倍数,又是5的倍数:__________。
10或2或5
13
2
62
65,61,51,15
60,50,10,56,16
60,50,10,65,15
60,50,10
解析:在按要求写数的同时,注意排列组合的顺序,这样可以做到不重复、不遗漏。
第4课时 3的倍数的特征
1.
观察下面的数表,回答问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
……
(1)
下面是数表中的其中一排数,按照上面数表中的规律,在这排数中圈出相应的数。
51
52
53
54
55
56
57
58
59
60
(2)
我发现:一个数(
)上的数的和是3的倍数,这个数就是3的倍数。
(3)
根据发现,2017应该圈上吗?为什么?
不应该圈上 因为它不是3的倍数
各位
2.
不计算,把小白兔要采的蘑菇涂上你喜欢的颜色。
3.
不计算,你能很快说出哪几道算式的得数没有余数吗?在没有余数的算式
下面的
里画“√”。
√
√
√
4.
下面的数字卡片摆出的数中哪些是3的倍数?若是,则在后面的
里画“√”;
若不是,则在
里填一个数字,使这个三位数成为3的倍数。
5.
在
里填一个数字,使每个数都是3的倍数,各有几种填法?分别填在括号
里。
8
(
)
62
(
)
75
(
)
9
9(
)
4
18(
)
16
6(
)
6
3
2
8
5
6
7
5
2
7
9
3
1,4,7
1,4,7
0,3,6,9
0,3,6,9
2,5,8
2,5,8
√
2
或
5
或
8
1
或
4
或
7
√
√
√
6.
李老师买了124本笔记本,要平均分给五年级三个班,至少要再买几本才能正
好分完?
7.
按要求填数。
(1)
在下面的
里填一个数字,使这个数既是2的倍数,又是3的倍数。
?
5
73
194
(2)
在下面的
里填一个数字,使这个数既是3的倍数,又是5的倍数。
16
90
258
1+2+4=7 7+2=9 至少要再买2本才能正好分完
8.
在
中,
里最小填几,这个数就是3的倍数?最大呢?
最小填1,最大填7 解析:2017个8不能被3整除,但2016个8可以被3整除,多的1个8凑成3的倍数即可,所以可以加上1或4或7,最小为1,最大为7。
4
2
或
8
1
或
4
或
7
5
0
0
第5课时 练
习
课
1.
把下面各数填入相应的圈里。
6
9
7
10
13
14
17
18
50
69
20
75
30
123
2的倍数
3的倍数
5的倍数
同时是2,3,5的倍数的数是(
)。
2.
判一判。
(1)
同时是2,3,5的倍数的数一定是偶数。
(
)
(2)
3个连续自然数的和一定是3的倍数。
(
)
(3)
偶数一定比奇数大。
(
)
(4)
2的倍数是偶数,3的倍数是奇数。
(
)
6,10,14,18,50,20,30
6,9,18,69,75,30,123
10,50,20,75,30
30
√
√
×
×
3.
1+6=7 7+2=9 至少要添2个苹果才能正好分完
4.
为了表彰在“学雷锋”活动中涌现出来的先进个人,齐老师买了5个文具盒和
一些钢笔作为奖品。
售货员找给齐老师的钱对不对?请说明理由。
不对 理由:因为5个文具盒正好是40元,一些钢笔的钱数的个位上是0或5,所以齐老师实际需付出的总钱数的个位上一定是0或5。因此售货员找回的钱数的个位上也一定是0或5,而不应该是4。
5.
选出两个数字组成一个两位数,分别满足下面的条件。
(1)
3的倍数:__________________。
(2)
同时是2和3的倍数:________。
(3)
同时是3和5的倍数:________。
(4)
同时是2和5的倍数:______________。
78,87,75,57
78
75
70,80,50
6.
圈出下表中9的倍数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
(1)
9的倍数都是3的倍数吗?
(2)
只看个位,能否判断一个数是不是9的倍数?如果不能,那么应该怎样判断?
是
不能 一个数各位上数的和是9的倍数,这个数就是9的倍数
7.
有一把钥匙能同时开4把锁,请你根据下面的信息找到钥匙的密码。
这把钥匙的密码是(
)。
解析:3的倍数的两位数且小于32的有12,15,18,21,24,27,30,其中是奇数的有15,21,27,再根据所有因数的和是32,可得这把钥匙的密码是21。
21
第6课时 质数和合数
1.
填一填。
(1)
一个数,如果只有(
)和(
)两个因数,那么这样的数叫做质
数(或素数)。
(2)
一个数,如果除了(
)还有别的因数,那么这样的数叫做合数。
(3)
20以内的质数有(
),其中(
)是偶数。
2.
判一判。
(1)
自然数不是质数就是合数。
(
)
(2)
所有的奇数都是质数,所有的偶数都是合数。
(
)
(3)
任意两个自然数的积都是合数。
(
)
(4)
两个质数的积一定是合数。
(
)
(5)
合数只有3个因数。
(
)
(6)
在所有质数中,只有2是偶数,其余都是奇数。
(
)
1
它本身
1和它本身
2,3,5,7,11,13,17,19
2
×
×
×
√
×
√
3.
将下面各数分别填入指定的方框里。
1
27
41
56
61
63
84
85
11
15
30
49
2
73
91
98
奇数
偶数
质数
合数
4.
猜一猜。(在括号里填上合适的数)
(
)
(
)
(1)
1,27,41,61,63,85,11,15,49,73
91
56,84,30,2,98
41,61,11,2,73
27,56,63,84,85,15,30,49,91,98
5
7
(2)
(
)
(
)
(
)
(
)
(3)
5.
想一想,填一填。
(1)
质数:
3,
里可以填(
)。
4
,
里可以填(
)。
(2)
合数:
7,
里可以填(
)。
5
,
里可以填(
)。
97
4
8
10
1,2,4,5,7,8
1,3,7
2,5,7,8
0,1,2,4,5,6,7,8
6.
欢欢用一根长38
cm的铁丝围成一个长方形,这个长方形的长和宽都是质数。
38÷2=19(cm
) 19=17+2 17×2=34(cm2)
解析:用38
cm长的铁丝围成一个长方形,即这个长方形的周长是38
cm,先用38÷2=19(cm),算出一条长和一条宽的长度,再根据长和宽都是质数,可以推出19=17+2,即长方形的长和宽分别是17
cm和2
cm,最后用“长×宽”算出长方形的面积是17×2=34(cm2)。
第7课时 解决问题
1.
仔细观察,填一填。(填“奇”或“偶”)
46 16 24 2
10 74 8 98
5 11 1 29
9 37 37 85
(1)
①
左图中的数都是(
)数,任意两个数相加的和是(
)数。
②
右图中的数都是(
)数,任意两个数相加的和是(
)数。
③
从左图中任意挑出一个数与右图中任意一个数相加,和是(
)数。
奇
偶
偶
奇
偶
奇
偶
偶
(2)
①
左图中任意两个数相乘的积是(
)数。
②
右图中任意两个数相乘的积是(
)数。
③
从左图中任意挑出一个数与右图中任意一个数相乘,积是(
)数。
2.
不计算,直接判断结果是奇数还是偶数。
46+27(
)
34+108(
)
13×72(
)
268×54(
)
89+415(
)
71×67(
)
143+2(
)
212×71(
)
偶
奇
偶
奇
偶
偶
奇数
偶数
偶数
偶数
偶数
奇数
奇数
偶数
3.
探索15的倍数的特征。
准备:我先写出一组15的倍数:15,30,
______________________________________……
观察:这些数个位上的数字都是(
),每个数各位上的数的和都是
(
)的倍数。
发现:15的倍数的特征是个位上的数字是(
)或(
),且各位上的数的
和是(
)的倍数。
4.
有45个苹果要分装在甲、乙两个袋子里。如果甲袋装的个数是偶数,那么乙袋
装的个数是偶数还是奇数?如果甲袋装的个数是奇数呢?
?
如果甲袋装的个数是偶数,那么乙袋装的个数是奇数;如果甲袋装的个数是奇数,那么乙袋装的个数是偶数
答案不唯一,如45,60,75,90,105
0或5
3
0
5
3
5.
你知道“哥德巴赫猜想”吗?请根据该结论把下面的合数写成两个质数的和。
28=(
)+(
)
40=(
)+(
)
56=(
)+(
)
100=(
)+(
)
答案不唯一
6.
有24个苹果,把它们放在9个盘子里,每个盘子里只能放奇数个,这件事你
能办到吗?为什么?
办不到 因为9个奇数的和一定还是奇数,不可能是偶数
17
11
17
23
53
3
97
3
