湘教版九年级上册数学单元冲刺卷附解析第1章 反比例函数(Word版)
文档属性
| 名称 | 湘教版九年级上册数学单元冲刺卷附解析第1章 反比例函数(Word版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 08:27:04 | ||
图片预览



文档简介
第1章
反比例函数
一、选择题(共15小题;共60分)
1.
函数
是
A.
一次函数
B.
二次函数
C.
反比例函数
D.
正比例函数
2.
已知蓄电池的电压为定值,使用蓄电池时,电流
(单位:)与电阻
(单位:)是反比例函数关系,它的图象如图所示.则用电阻
表示电流
的函数表达式为
A.
B.
C.
D.
3.
反比例函数
的图象经过点
,,当
时,
的取值范围是
A.
B.
C.
D.
4.
某闭合电路中,电源的电压为定值,电流强度
与电阻
成反比例关系,其函数图象如图所示,则电流强度
与电阻
的函数解析式是
A.
B.
C.
D.
5.
若函数
是反比例函数,则
的值为
A.
B.
C.
或
D.
或
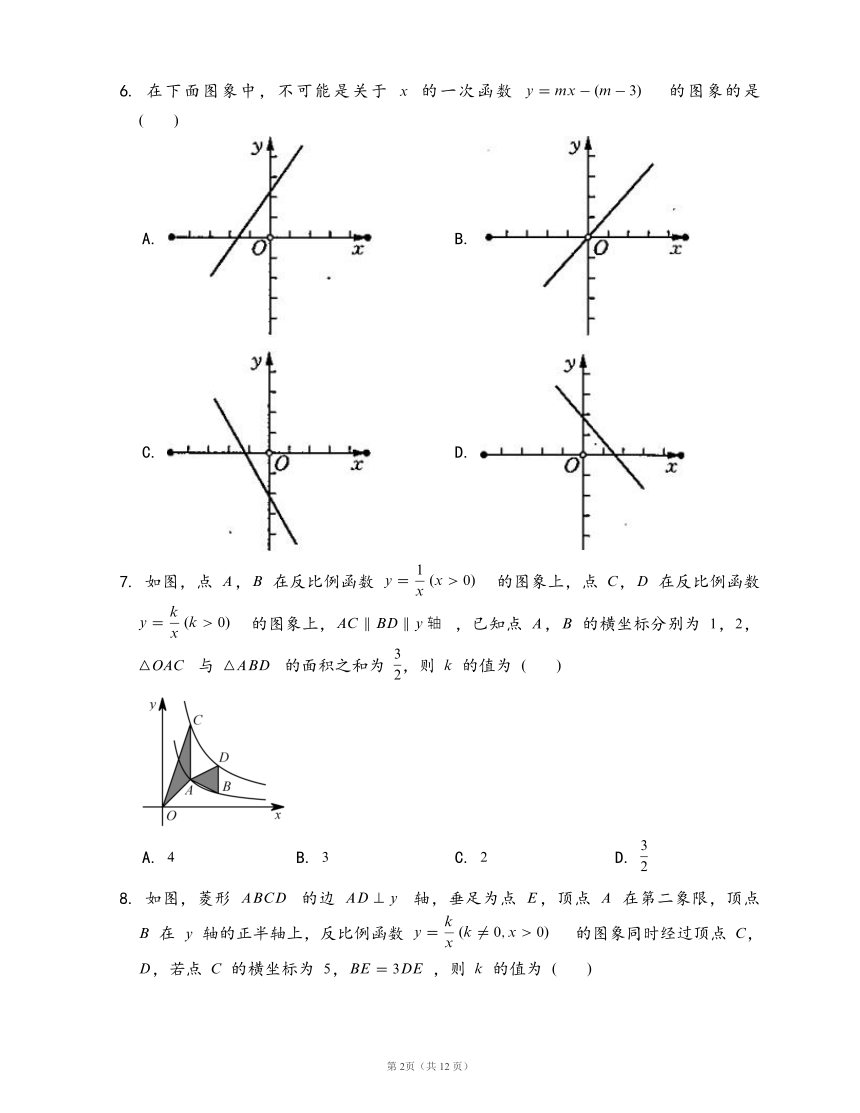
6.
在下面图象中,不可能是关于
的一次函数
的图象的是
A.
B.
C.
D.
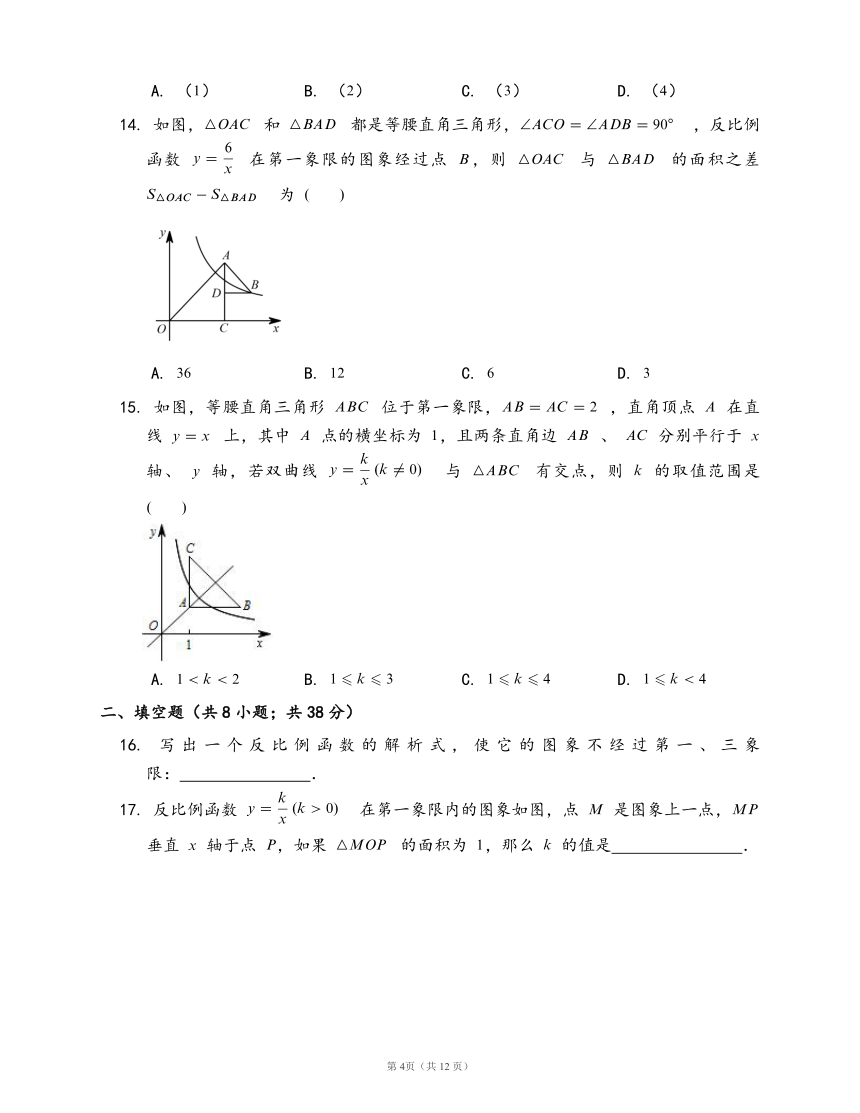
7.
如图,点
,
在反比例函数
的图象上,点
,
在反比例函数
的图象上,,已知点
,
的横坐标分别为
,,
与
的面积之和为
,则
的值为
A.
B.
C.
D.
8.
如图,菱形
的边
轴,垂足为点
,顶点
在第二象限,顶点
在
轴的正半轴上,反比例函数
的图象同时经过顶点
,,若点
的横坐标为
,,则
的值为
A.
B.
C.
D.
9.
若函数
是反比例函数,则
A.
B.
C.
D.
10.
下列函数:①
;②
;③
;④
,反比例函数有
A.
个
B.
个
C.
个
D.
个
11.
在反比例函数
图象上有两点
,,,,则
的取值范围是
A.
B.
C.
D.
12.
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压
与气球体积
之间是反比例函数关系,其函数图象如图所示.当气球内的气压大于
(含
)时,气球将爆炸.为了安全起见,气球的体积应
A.
小于
B.
大于
C.
小于
D.
大于
13.
如图,双曲线
的一个分支为
A.
()
B.
()
C.
()
D.
()
14.
如图,
和
都是等腰直角三角形,,反比例函数
在第一象限的图象经过点
,则
与
的面积之差
为
A.
B.
C.
D.
15.
如图,等腰直角三角形
位于第一象限,,直角顶点
在直线
上,其中
点的横坐标为
,且两条直角边
、
分别平行于
轴、
轴,若双曲线
与
有交点,则
的取值范围是
A.
B.
C.
D.
二、填空题(共8小题;共38分)
16.
写出一个反比例函数的解析式,使它的图象不经过第一、三象限:
?.
17.
反比例函数
在第一象限内的图象如图,点
是图象上一点,
垂直
轴于点
,如果
的面积为
,那么
的值是
?.
18.
为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量
与时间
的函数关系如图所示.已知,药物燃烧阶段,
与
成正比例,燃完后
与
成反比例.现测得药物
分钟燃完,此时教室内每立方米空气含药量为
.当每立方米空气中含药量低于
时,对人体才能无毒害作用.那么从消毒开始,经过
?
分钟后教室内的空气才能达到安全要求.
19.
已知
,
都在
图象上,若
,则
的值为
?.
20.
若
是反比例函数,则
的值为
?.
21.
如图,
、
是等腰直角三角形,点
、
在函数
的图象上,斜边
、
都在
轴上,则点
的坐标是
?.
22.
两个反比例函数
,
在第一象限内的图象如图所示,点
,,,,
在反比例函数
图象上,它们的横坐标分别是
,,,,,纵坐标分别是
,,,,共
个连续奇数,过点
,,,,
分别作
轴的平行线,与
的图象交点依次是
,,,,,则
?,三角形
的面积为
?.
23.
如图,直线
与双曲线
在第一象限内的图象交于一点
,与
负半轴交与点
.点
是该双曲线在第一象限内图象上的一点,且
点在
点的右侧,分别过点
,
作
轴的垂线,垂足分别为点
,,连接
.则
的面积
?
的面积(填“”、“”或“”).
三、解答题(共4小题;共52分)
24.
某蓄水池的排水管道每小时排水
,
可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管道,使每小时的排水量达到
,将满池水排空所需时间为
,求
与
之间的函数关系式;
(3)如果准备在
内将满池水排空,那第每小时排水量到少为多少?
(4)已知排水管的最大排水量为每小时
,那么最少多长时间可将满池水全部排空?
25.
已知反比例函数
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求
的取值范围;
(2)如图,
为坐标原点,点
在该反比例函数位于第一象限的图象上,点
与点
关于
轴对称,若
的面积为
,求
的值.
26.
已知
,其中
与
成反比例,
与
成正比例,且当
时,;当
时,.求当
时,
的值.
27.
已知直线
与
轴交于点
,它与反比例函数
的图象在第一象限内交于点
,直线
经过点
,且与
轴交于点
,若
的面积为
,求直线
的解析式.
答案
第一部分
1.
C
2.
D
3.
B
【解析】
比例函数
的图象经过点
,
,解得:.
反比例函数的解析式为:.
,
当
时,
随
的增大而增大,
时,;
时,,
的取值范围是
.
4.
C
【解析】将
代入反比例函数的解析式
,利用待定系数法求得函数解析式
.
5.
A
6.
C
7.
B
8.
C
9.
A
【解析】
是反比例函数,
解得
.
10.
B
【解析】①
是正比例函数;②
是正比例函数;③
是反比例函数;④
不是反比例函数.
11.
B
【解析】
时,,说明反比例函数图象位于一三象限,故
,
所以
.
12.
D
13.
D
【解析】
在
中,,
它的两个分支分别位于第一、三象限,排除①②;
又当
时,,排除③;
应该是④.
14.
D
【解析】设
和
的直角边长分别为
、
.
则点
的坐标为
.
点
在反比例函数
的第一象限图象上,
.
.
15.
C
【解析】函数图象在点
与
的中点间变动.
如图,设直线
与
交于
点,分别过
、
两点作
轴的垂线,垂足为
、
,
交
于
,
点的横坐标为
,
点在直线
上,
,
又
,,,
,,且
为等腰直角三角形,
的中点坐标为
,即为
,
点
满足直线
,
点
即为
点坐标,
点坐标为
,
,或
,
当双曲线与
有唯一交点时,.
第二部分
16.
(答案不唯一)
17.
18.
19.
【解析】根据
即可得到.
20.
21.
【解析】分别过
、
作
轴垂线垂足为
、
,
则
,设
的纵坐标为
,
则
,代入函数解析式
,
解得
.
.
22.
,
23.
【解析】连接
,,
则
,
,点
是该双曲线在第一象限内图象上的一点,且
点在
点的右侧,
,
,
,
,,
,
,即
,
故答案为
.
第三部分
24.
(1)
蓄水池的容积是:.
??????(2)
与
之间的关系式为
.
??????(3)
,解不等式得,,
即每小时的排水量至少为
.
??????(4)
当
时,由
得
,
即最少用
可将满池水全部排空.
25.
(1)
根据反比例函数的图象关于原点成中心对称知,该函数图象的另一支在第三象限,且
,则
.
??????(2)
如图,记
与
轴交点为
.
点
与点
关于
轴对称,若
的面积为
,
的面积为
.
设
,则
,
解得
.
26.
设
.
当
时,;当
时,
,
.
当
时,
.
27.
由题意可得
.
联立方程组
解得
因为点
在第一象限,
所以
.
设点
,则
.
,
解得
.即
.
当
时,直线
的解析式为
;
当
时,设直线
的解析式为
,
则
解得
所以直线
的解析式为
.
第7页(共12
页)
反比例函数
一、选择题(共15小题;共60分)
1.
函数
是
A.
一次函数
B.
二次函数
C.
反比例函数
D.
正比例函数
2.
已知蓄电池的电压为定值,使用蓄电池时,电流
(单位:)与电阻
(单位:)是反比例函数关系,它的图象如图所示.则用电阻
表示电流
的函数表达式为
A.
B.
C.
D.
3.
反比例函数
的图象经过点
,,当
时,
的取值范围是
A.
B.
C.
D.
4.
某闭合电路中,电源的电压为定值,电流强度
与电阻
成反比例关系,其函数图象如图所示,则电流强度
与电阻
的函数解析式是
A.
B.
C.
D.
5.
若函数
是反比例函数,则
的值为
A.
B.
C.
或
D.
或
6.
在下面图象中,不可能是关于
的一次函数
的图象的是
A.
B.
C.
D.
7.
如图,点
,
在反比例函数
的图象上,点
,
在反比例函数
的图象上,,已知点
,
的横坐标分别为
,,
与
的面积之和为
,则
的值为
A.
B.
C.
D.
8.
如图,菱形
的边
轴,垂足为点
,顶点
在第二象限,顶点
在
轴的正半轴上,反比例函数
的图象同时经过顶点
,,若点
的横坐标为
,,则
的值为
A.
B.
C.
D.
9.
若函数
是反比例函数,则
A.
B.
C.
D.
10.
下列函数:①
;②
;③
;④
,反比例函数有
A.
个
B.
个
C.
个
D.
个
11.
在反比例函数
图象上有两点
,,,,则
的取值范围是
A.
B.
C.
D.
12.
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压
与气球体积
之间是反比例函数关系,其函数图象如图所示.当气球内的气压大于
(含
)时,气球将爆炸.为了安全起见,气球的体积应
A.
小于
B.
大于
C.
小于
D.
大于
13.
如图,双曲线
的一个分支为
A.
()
B.
()
C.
()
D.
()
14.
如图,
和
都是等腰直角三角形,,反比例函数
在第一象限的图象经过点
,则
与
的面积之差
为
A.
B.
C.
D.
15.
如图,等腰直角三角形
位于第一象限,,直角顶点
在直线
上,其中
点的横坐标为
,且两条直角边
、
分别平行于
轴、
轴,若双曲线
与
有交点,则
的取值范围是
A.
B.
C.
D.
二、填空题(共8小题;共38分)
16.
写出一个反比例函数的解析式,使它的图象不经过第一、三象限:
?.
17.
反比例函数
在第一象限内的图象如图,点
是图象上一点,
垂直
轴于点
,如果
的面积为
,那么
的值是
?.
18.
为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量
与时间
的函数关系如图所示.已知,药物燃烧阶段,
与
成正比例,燃完后
与
成反比例.现测得药物
分钟燃完,此时教室内每立方米空气含药量为
.当每立方米空气中含药量低于
时,对人体才能无毒害作用.那么从消毒开始,经过
?
分钟后教室内的空气才能达到安全要求.
19.
已知
,
都在
图象上,若
,则
的值为
?.
20.
若
是反比例函数,则
的值为
?.
21.
如图,
、
是等腰直角三角形,点
、
在函数
的图象上,斜边
、
都在
轴上,则点
的坐标是
?.
22.
两个反比例函数
,
在第一象限内的图象如图所示,点
,,,,
在反比例函数
图象上,它们的横坐标分别是
,,,,,纵坐标分别是
,,,,共
个连续奇数,过点
,,,,
分别作
轴的平行线,与
的图象交点依次是
,,,,,则
?,三角形
的面积为
?.
23.
如图,直线
与双曲线
在第一象限内的图象交于一点
,与
负半轴交与点
.点
是该双曲线在第一象限内图象上的一点,且
点在
点的右侧,分别过点
,
作
轴的垂线,垂足分别为点
,,连接
.则
的面积
?
的面积(填“”、“”或“”).
三、解答题(共4小题;共52分)
24.
某蓄水池的排水管道每小时排水
,
可将满池水全部排空.
(1)蓄水池的容积是多少?
(2)如果增加排水管道,使每小时的排水量达到
,将满池水排空所需时间为
,求
与
之间的函数关系式;
(3)如果准备在
内将满池水排空,那第每小时排水量到少为多少?
(4)已知排水管的最大排水量为每小时
,那么最少多长时间可将满池水全部排空?
25.
已知反比例函数
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求
的取值范围;
(2)如图,
为坐标原点,点
在该反比例函数位于第一象限的图象上,点
与点
关于
轴对称,若
的面积为
,求
的值.
26.
已知
,其中
与
成反比例,
与
成正比例,且当
时,;当
时,.求当
时,
的值.
27.
已知直线
与
轴交于点
,它与反比例函数
的图象在第一象限内交于点
,直线
经过点
,且与
轴交于点
,若
的面积为
,求直线
的解析式.
答案
第一部分
1.
C
2.
D
3.
B
【解析】
比例函数
的图象经过点
,
,解得:.
反比例函数的解析式为:.
,
当
时,
随
的增大而增大,
时,;
时,,
的取值范围是
.
4.
C
【解析】将
代入反比例函数的解析式
,利用待定系数法求得函数解析式
.
5.
A
6.
C
7.
B
8.
C
9.
A
【解析】
是反比例函数,
解得
.
10.
B
【解析】①
是正比例函数;②
是正比例函数;③
是反比例函数;④
不是反比例函数.
11.
B
【解析】
时,,说明反比例函数图象位于一三象限,故
,
所以
.
12.
D
13.
D
【解析】
在
中,,
它的两个分支分别位于第一、三象限,排除①②;
又当
时,,排除③;
应该是④.
14.
D
【解析】设
和
的直角边长分别为
、
.
则点
的坐标为
.
点
在反比例函数
的第一象限图象上,
.
.
15.
C
【解析】函数图象在点
与
的中点间变动.
如图,设直线
与
交于
点,分别过
、
两点作
轴的垂线,垂足为
、
,
交
于
,
点的横坐标为
,
点在直线
上,
,
又
,,,
,,且
为等腰直角三角形,
的中点坐标为
,即为
,
点
满足直线
,
点
即为
点坐标,
点坐标为
,
,或
,
当双曲线与
有唯一交点时,.
第二部分
16.
(答案不唯一)
17.
18.
19.
【解析】根据
即可得到.
20.
21.
【解析】分别过
、
作
轴垂线垂足为
、
,
则
,设
的纵坐标为
,
则
,代入函数解析式
,
解得
.
.
22.
,
23.
【解析】连接
,,
则
,
,点
是该双曲线在第一象限内图象上的一点,且
点在
点的右侧,
,
,
,
,,
,
,即
,
故答案为
.
第三部分
24.
(1)
蓄水池的容积是:.
??????(2)
与
之间的关系式为
.
??????(3)
,解不等式得,,
即每小时的排水量至少为
.
??????(4)
当
时,由
得
,
即最少用
可将满池水全部排空.
25.
(1)
根据反比例函数的图象关于原点成中心对称知,该函数图象的另一支在第三象限,且
,则
.
??????(2)
如图,记
与
轴交点为
.
点
与点
关于
轴对称,若
的面积为
,
的面积为
.
设
,则
,
解得
.
26.
设
.
当
时,;当
时,
,
.
当
时,
.
27.
由题意可得
.
联立方程组
解得
因为点
在第一象限,
所以
.
设点
,则
.
,
解得
.即
.
当
时,直线
的解析式为
;
当
时,设直线
的解析式为
,
则
解得
所以直线
的解析式为
.
第7页(共12
页)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
