24.1.4 圆周角(第三课时 圆内接四边形)同步练习题(含答案)
文档属性
| 名称 | 24.1.4 圆周角(第三课时 圆内接四边形)同步练习题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
24.1.4 圆周角(第三课时 圆内接四边形)
练习
一、单选题(共10小题)
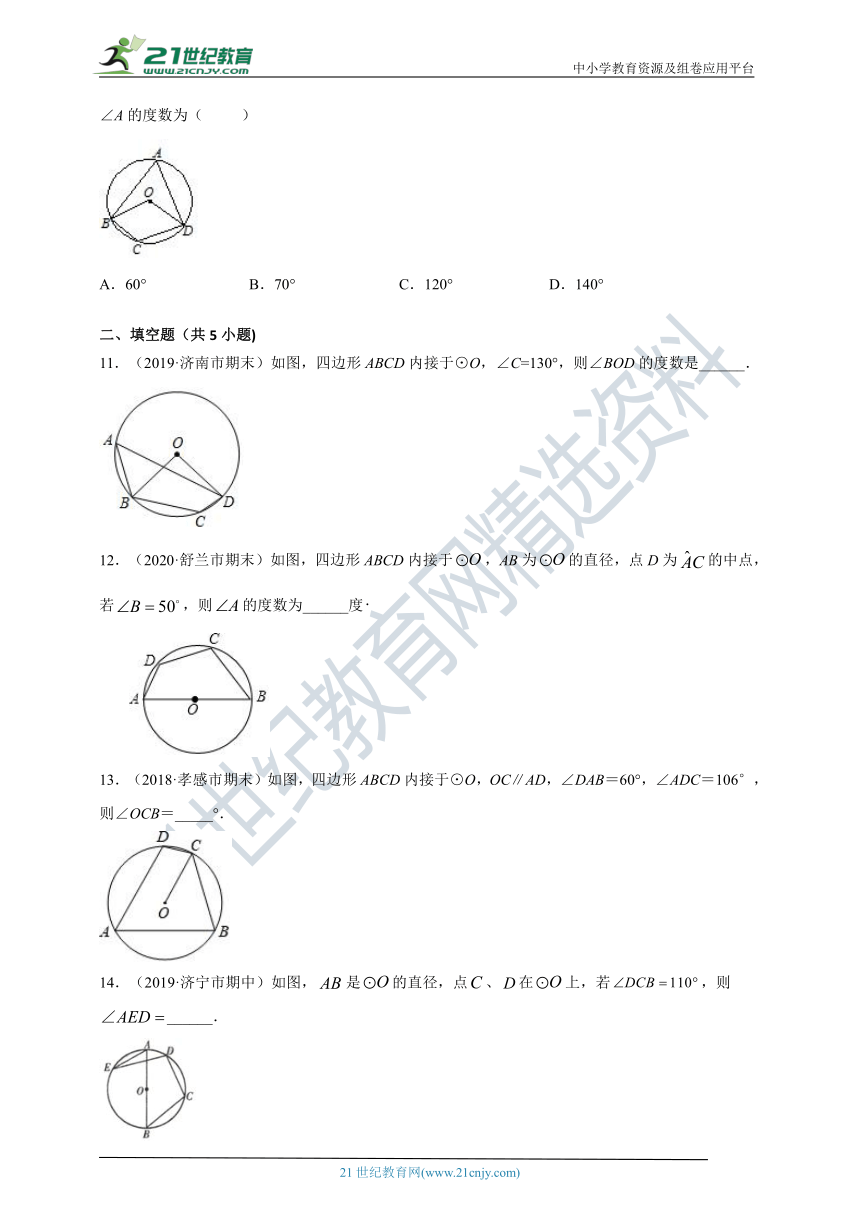
1.(2019·昆明市期末)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.120° C.100° D.90°
2.(2019·蚌埠市期中)如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A. B. C. D.
3.(2019·苏州市期中)如图,四边形是半圆的内接四边形,是直径,.若,则的度数等于( )
A. B. C. D.
4.(2019·金昌市期中)如图,四边形 ABCD 是⊙O的内接四边形,若∠BOD=88°,则∠BCD 的度数是
A.88° B.92° C.106° D.136°
5.(2020·包头市期末)如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
6.(2019·昆明市期中)如图,扇形AOB的圆心角为142°,点C是弧AB上一点,则∠ACB的度数是( )
A.38° B.120° C.109° D.119°
7.(2019·始兴县期末)圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60° B.80° C.100° D.120°
8.(2019·宁波市期中)如图,AB是半圆O的直径,C、D是半圆弧上两点,∠D=115°,则∠CAB=( )
A.55° B.45° C.35° D.25°
9.(2020·抚顺市期末)已知圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则∠D的大小是( )
A.45° B.60° C.90° D.135°
10.(2018·金华市期末)如图,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则∠A的度数为( )
A.60° B.70° C.120° D.140°
二、填空题(共5小题)
11.(2019·济南市期末)如图,四边形ABCD内接于⊙O,∠C=130°,则∠BOD的度数是______.
12.(2020·舒兰市期末)如图,四边形ABCD内接于,AB为的直径,点D为的中点,若,则的度数为______度
13.(2018·孝感市期末)如图,四边形ABCD内接于⊙O,OC∥AD,∠DAB=60°,∠ADC=106°,则∠OCB=_____°.
14.(2019·济宁市期中)如图,是的直径,点、在上,若,则______.
15.(2019·宿迁市期中)一条弦把圆分成1:2两部分,那么这条弦所对的圆周角的度数为_____.
三、解答题(共2小题)
16.(2018·泰州市期中)如图,在△ABC中,∠A=68°,以AB为直径的⊙O与AC、BC分别相交于点D、E,连接DE.
(1)求∠CED的度数.
(2)若DE=BE,求∠C的度数.
17.(2019·绍兴市期中)如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E.
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE
答案
一、单选题(共10小题)
1.B.2.C3.A4.D5.B6.C7.C8.D9.C.10.A
二、填空题(共5小题)
11.【答案】100°.【详解】∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,∵∠C=130°,
∴∠A=50°,∴∠BOD=2∠A=100°,故答案为100°.
12.【答案】65【解析】连接OD、OC,
∵点D为的中点,
∴∠AOD=∠COD,
∵∠B=50°,
∴∠AOC=100°,
∴∠AOD=∠COD=50°,
∴∠A=∠ODA=65°,
故答案为65.
13.【答案】46【详解】解:∵OC∥AD,
∴∠OCD=180°-∠ADC=74°, ∵四边形ABCD内接于⊙O,
∴∠BCD=180°-∠DAB=120°,
∴∠OCB=∠BCD-∠OCD=46°,故答案为:46.
14.【答案】20°.【详解】
连接BE,因为是的直径
所以∠AEB=90°因为点C、D在⊙O上,∠DCB=110°
所以∠BED=180°-∠DCB=70°
所以∠AEB-∠BED=20°故答案为20°
15.【答案】60°或120°.【详解】解:如图,连接OA、OB.
弦AB将⊙O分为1:2两部分,则∠AOB=×360°=120°;
∴∠ACB=∠AOB=60°,∠ADB=180°﹣∠60=120°;
故这条弦所对的圆周角的度数为60°或120°.
故答案为:60°或120°
三、解答题(共2小题)
16.【答案】(1)∠CED=68°.(2)56°.【详解】解:(1)∵四边形ABED 圆内接四边形,∴∠CED=∠A.
∵∠A=68°,∴∠CED=68°.
(2)连接AE.∵DE=BD,∴=,∴∠DAE=∠EAB=∠CAB=34°.
∵AB是直径,∴∠AEB=90°,∴∠AEC=90°,∴∠C=90°﹣∠DAE=90°﹣34°=56°.
17.【答案】(1) ∠CBE=86°;(2)证明见解析.【解析】(1) ∵ 四边形ABCD内接于⊙O,
∴ ∠ADC+ ∠ABC= 180°.
又∵ ∠ADC= 86°,
∴ ∠ABC= 94°,
∴ ∠CBE=180° - 94°=86°.
(2)∵ AC=EC,
∴ ∠E=∠CAE ,
∵ AC平分∠BAD,
∴ ∠DAC=∠CAB ,
∴ ∠DAC= ∠E.
∵ 四边形ABCD内接于⊙O,
∴ ∠ADC+ ∠ABC= 180°,
又∵∠CBE+∠ABC = 180°, ,
∴ ∠ADC= ∠CBE,
∴ △ADC ≌ △EBC ,
∴ AD=BE .
_21?????????è?????(www.21cnjy.com)_
第二十四章 圆
24.1.4 圆周角(第三课时 圆内接四边形)
练习
一、单选题(共10小题)
1.(2019·昆明市期末)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.120° C.100° D.90°
2.(2019·蚌埠市期中)如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
A. B. C. D.
3.(2019·苏州市期中)如图,四边形是半圆的内接四边形,是直径,.若,则的度数等于( )
A. B. C. D.
4.(2019·金昌市期中)如图,四边形 ABCD 是⊙O的内接四边形,若∠BOD=88°,则∠BCD 的度数是
A.88° B.92° C.106° D.136°
5.(2020·包头市期末)如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.105° C.100° D.95°
6.(2019·昆明市期中)如图,扇形AOB的圆心角为142°,点C是弧AB上一点,则∠ACB的度数是( )
A.38° B.120° C.109° D.119°
7.(2019·始兴县期末)圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60° B.80° C.100° D.120°
8.(2019·宁波市期中)如图,AB是半圆O的直径,C、D是半圆弧上两点,∠D=115°,则∠CAB=( )
A.55° B.45° C.35° D.25°
9.(2020·抚顺市期末)已知圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则∠D的大小是( )
A.45° B.60° C.90° D.135°
10.(2018·金华市期末)如图,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则∠A的度数为( )
A.60° B.70° C.120° D.140°
二、填空题(共5小题)
11.(2019·济南市期末)如图,四边形ABCD内接于⊙O,∠C=130°,则∠BOD的度数是______.
12.(2020·舒兰市期末)如图,四边形ABCD内接于,AB为的直径,点D为的中点,若,则的度数为______度
13.(2018·孝感市期末)如图,四边形ABCD内接于⊙O,OC∥AD,∠DAB=60°,∠ADC=106°,则∠OCB=_____°.
14.(2019·济宁市期中)如图,是的直径,点、在上,若,则______.
15.(2019·宿迁市期中)一条弦把圆分成1:2两部分,那么这条弦所对的圆周角的度数为_____.
三、解答题(共2小题)
16.(2018·泰州市期中)如图,在△ABC中,∠A=68°,以AB为直径的⊙O与AC、BC分别相交于点D、E,连接DE.
(1)求∠CED的度数.
(2)若DE=BE,求∠C的度数.
17.(2019·绍兴市期中)如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E.
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE
答案
一、单选题(共10小题)
1.B.2.C3.A4.D5.B6.C7.C8.D9.C.10.A
二、填空题(共5小题)
11.【答案】100°.【详解】∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,∵∠C=130°,
∴∠A=50°,∴∠BOD=2∠A=100°,故答案为100°.
12.【答案】65【解析】连接OD、OC,
∵点D为的中点,
∴∠AOD=∠COD,
∵∠B=50°,
∴∠AOC=100°,
∴∠AOD=∠COD=50°,
∴∠A=∠ODA=65°,
故答案为65.
13.【答案】46【详解】解:∵OC∥AD,
∴∠OCD=180°-∠ADC=74°, ∵四边形ABCD内接于⊙O,
∴∠BCD=180°-∠DAB=120°,
∴∠OCB=∠BCD-∠OCD=46°,故答案为:46.
14.【答案】20°.【详解】
连接BE,因为是的直径
所以∠AEB=90°因为点C、D在⊙O上,∠DCB=110°
所以∠BED=180°-∠DCB=70°
所以∠AEB-∠BED=20°故答案为20°
15.【答案】60°或120°.【详解】解:如图,连接OA、OB.
弦AB将⊙O分为1:2两部分,则∠AOB=×360°=120°;
∴∠ACB=∠AOB=60°,∠ADB=180°﹣∠60=120°;
故这条弦所对的圆周角的度数为60°或120°.
故答案为:60°或120°
三、解答题(共2小题)
16.【答案】(1)∠CED=68°.(2)56°.【详解】解:(1)∵四边形ABED 圆内接四边形,∴∠CED=∠A.
∵∠A=68°,∴∠CED=68°.
(2)连接AE.∵DE=BD,∴=,∴∠DAE=∠EAB=∠CAB=34°.
∵AB是直径,∴∠AEB=90°,∴∠AEC=90°,∴∠C=90°﹣∠DAE=90°﹣34°=56°.
17.【答案】(1) ∠CBE=86°;(2)证明见解析.【解析】(1) ∵ 四边形ABCD内接于⊙O,
∴ ∠ADC+ ∠ABC= 180°.
又∵ ∠ADC= 86°,
∴ ∠ABC= 94°,
∴ ∠CBE=180° - 94°=86°.
(2)∵ AC=EC,
∴ ∠E=∠CAE ,
∵ AC平分∠BAD,
∴ ∠DAC=∠CAB ,
∴ ∠DAC= ∠E.
∵ 四边形ABCD内接于⊙O,
∴ ∠ADC+ ∠ABC= 180°,
又∵∠CBE+∠ABC = 180°, ,
∴ ∠ADC= ∠CBE,
∴ △ADC ≌ △EBC ,
∴ AD=BE .
_21?????????è?????(www.21cnjy.com)_
同课章节目录
