人教版八年级数学上册 13.2.1画轴对称图形 能力提升卷(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 13.2.1画轴对称图形 能力提升卷(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 365.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-24 21:13:00 | ||
图片预览



文档简介
人教版八年级数学上册
13.2.1画轴对称图形
能力提升卷
一、选择题(共10小题,3
10=30)
1.小明站在平面镜前,看见镜中的自己胸前球衣的号码是
,则实际的号码为( )
2.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
3.如图,与正六边形ABCDEF关于直线l成轴对称的图形是六边形A′B′C′D′E′F′,则下列判断错误的是( )
A.AB=A′B′
B.BC∥B′C′
C.直线l⊥BB′
D.∠A′=120°
4.如图,在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使整个阴影部分组成的图形是轴对称图形,则符合条件的小正方形有( )
A.1个
B.2个
C.3个
D.4个
5.如图,在小正三角形组成的网格中,已有6个小正三角形涂灰,还需涂灰n个小正三角形,使它们与原来被涂灰的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.10
B.6
C.3
D.2
6.
已知两条互不平行的线段AB和A′B′关于直线1对称,AB和A′B′所在的直线交于点P,下面四个结论:①AB
=A′B′;②点P在直线1上
;③若A、A′是对应点,则直
线1垂直平分线段AA′;
④若B、B′是对应
点,则PB=PB′,其中正确的是( )
A.①③④
B.③④
C.①②
D.①②③④
7.在如图所示的3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,方法有( )
A.1种
B.2种
C.3种
D.4种
8.如图,在△ABC中,分别以点A和点B为圆心,大于
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
A.
7
B.
14
C.
17
D.
20
9.如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论,其中正确的个数是( )
①
∠DEF=∠DFE;②AE=AF;③AD垂直平分EF;④EF垂
直平分AD.
A.1个
B.2个
C.3个
D.4个
10.如图,阴影部分是由5个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分),其中不是轴对称图形的是( )
A.
B.
C.
D
二.填空题(共8小题,3
8=24)
11.
由一个平面图形可以得到它关于某条直线对称的图形,这个图形与原图形的_________、___________完全一样.
12.
如图,在正三角形网格中,已有两个小三角形被涂黑,再将图中其余的小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有________种.
13.如图,AB左边是计算器上的数字“5”,若以直线AB为对称轴,那么它的轴对称图形是数字_________.
14.如图所示,观察规律并填空: _______.
15.给出下列图形:
线段;
射线;
直线;
圆;
等腰直角三角形;
等边三角形;
等腰梯形.其中只有一条对称轴的图形有__________
(填序号)
16.17.
在等腰三角形、等边三角形、直角三角形、等腰直角三角形等特殊的三角形中,是轴对称图形的有______个
17.
如图是一台球桌面示意图,图
中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是________.
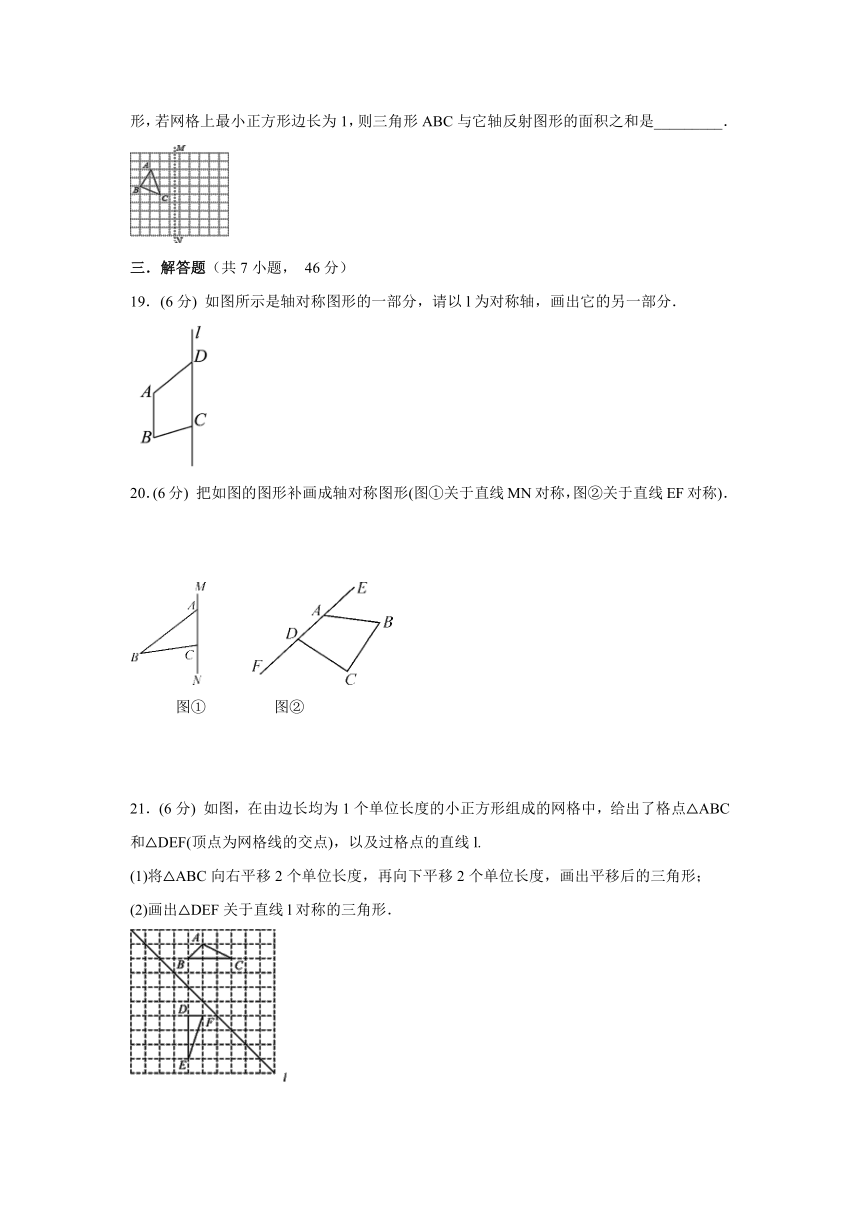
18.在如图的正方形网格中有一个三角形ABC,作出三角形ABC关于直线MN的轴反射图形,若网格上最小正方形边长为1,则三角形ABC与它轴反射图形的面积之和是_________.
三.解答题(共7小题,
46分)
19.(6分)
如图所示是轴对称图形的一部分,请以l为对称轴,画出它的另一部分.
20.(6分)
把如图的图形补画成轴对称图形(图①关于直线MN对称,图②关于直线EF对称).
图①
图②
21.(6分)
如图,在由边长均为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移2个单位长度,再向下平移2个单位长度,画出平移后的三角形;
(2)画出△DEF关于直线l对称的三角形.
22.(6分)
在如图①②③中各补一个小正方形,使其成为不同的轴对称图形.
①
②
③
23.(6分)
如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格点为顶点的三角形,这样的三角形共有多少个?画出图形.
24.(8分)
在∠AOB内部有一点P,分别作出点P关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=10
cm.求△PMN的周长.
25.(8分)
如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN、EF所夹锐角α的数量关系.
参考答案
1-5CABCC
6-10DCCCD
11.
形状;大小
12.
3
13.
2;5
14.
15.
②⑤⑦
16.
3
17.
①
18.
5
19.
解:如图所示。
20.
解:如图①②.
图①
图②
21.
解:(1)如图,△A′B′C′
即为所求.
(2)如图,△D′E′F′
即为所求.
22.
解:如图①②③.
图①
图②
图③
23.
解:如图,与△ABC成轴对称且以格点为顶点的三角形有5个,分别为△BCD,△BFH,△ADC,△AEF,△CGH.
24.
解:如图,点P1,P2即为所求,
∵点P1和点P关于OA对称,
∴OA垂直平分P1P.
又∵点M在AO上,
∴MP1=MP,同理可证PN=P2N,
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2=10
cm.
25.
解:(1)如图,连接B′B″.
作线段B'B″的垂直平分线EF.
则直线EF是△A′B′C′和△A″B″C″的对称轴.
(2)连接B′O.
∵△ABC和△A'B'C'关于直线MN对称,
∴∠BOM=∠B'OM.
又∵△A'B'C'和△A″B″C″关于直线EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α
即∠BOB″=2α.
13.2.1画轴对称图形
能力提升卷
一、选择题(共10小题,3
10=30)
1.小明站在平面镜前,看见镜中的自己胸前球衣的号码是
,则实际的号码为( )
2.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
3.如图,与正六边形ABCDEF关于直线l成轴对称的图形是六边形A′B′C′D′E′F′,则下列判断错误的是( )
A.AB=A′B′
B.BC∥B′C′
C.直线l⊥BB′
D.∠A′=120°
4.如图,在4×4的正方形网格中,已将图中的四个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使整个阴影部分组成的图形是轴对称图形,则符合条件的小正方形有( )
A.1个
B.2个
C.3个
D.4个
5.如图,在小正三角形组成的网格中,已有6个小正三角形涂灰,还需涂灰n个小正三角形,使它们与原来被涂灰的小正三角形组成的新图案恰有三条对称轴,则n的最小值为( )
A.10
B.6
C.3
D.2
6.
已知两条互不平行的线段AB和A′B′关于直线1对称,AB和A′B′所在的直线交于点P,下面四个结论:①AB
=A′B′;②点P在直线1上
;③若A、A′是对应点,则直
线1垂直平分线段AA′;
④若B、B′是对应
点,则PB=PB′,其中正确的是( )
A.①③④
B.③④
C.①②
D.①②③④
7.在如图所示的3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,方法有( )
A.1种
B.2种
C.3种
D.4种
8.如图,在△ABC中,分别以点A和点B为圆心,大于
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
A.
7
B.
14
C.
17
D.
20
9.如图,△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论,其中正确的个数是( )
①
∠DEF=∠DFE;②AE=AF;③AD垂直平分EF;④EF垂
直平分AD.
A.1个
B.2个
C.3个
D.4个
10.如图,阴影部分是由5个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分),其中不是轴对称图形的是( )
A.
B.
C.
D
二.填空题(共8小题,3
8=24)
11.
由一个平面图形可以得到它关于某条直线对称的图形,这个图形与原图形的_________、___________完全一样.
12.
如图,在正三角形网格中,已有两个小三角形被涂黑,再将图中其余的小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有________种.
13.如图,AB左边是计算器上的数字“5”,若以直线AB为对称轴,那么它的轴对称图形是数字_________.
14.如图所示,观察规律并填空: _______.
15.给出下列图形:
线段;
射线;
直线;
圆;
等腰直角三角形;
等边三角形;
等腰梯形.其中只有一条对称轴的图形有__________
(填序号)
16.17.
在等腰三角形、等边三角形、直角三角形、等腰直角三角形等特殊的三角形中,是轴对称图形的有______个
17.
如图是一台球桌面示意图,图
中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是________.
18.在如图的正方形网格中有一个三角形ABC,作出三角形ABC关于直线MN的轴反射图形,若网格上最小正方形边长为1,则三角形ABC与它轴反射图形的面积之和是_________.
三.解答题(共7小题,
46分)
19.(6分)
如图所示是轴对称图形的一部分,请以l为对称轴,画出它的另一部分.
20.(6分)
把如图的图形补画成轴对称图形(图①关于直线MN对称,图②关于直线EF对称).
图①
图②
21.(6分)
如图,在由边长均为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移2个单位长度,再向下平移2个单位长度,画出平移后的三角形;
(2)画出△DEF关于直线l对称的三角形.
22.(6分)
在如图①②③中各补一个小正方形,使其成为不同的轴对称图形.
①
②
③
23.(6分)
如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格点为顶点的三角形,这样的三角形共有多少个?画出图形.
24.(8分)
在∠AOB内部有一点P,分别作出点P关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,若P1P2=10
cm.求△PMN的周长.
25.(8分)
如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN、EF所夹锐角α的数量关系.
参考答案
1-5CABCC
6-10DCCCD
11.
形状;大小
12.
3
13.
2;5
14.
15.
②⑤⑦
16.
3
17.
①
18.
5
19.
解:如图所示。
20.
解:如图①②.
图①
图②
21.
解:(1)如图,△A′B′C′
即为所求.
(2)如图,△D′E′F′
即为所求.
22.
解:如图①②③.
图①
图②
图③
23.
解:如图,与△ABC成轴对称且以格点为顶点的三角形有5个,分别为△BCD,△BFH,△ADC,△AEF,△CGH.
24.
解:如图,点P1,P2即为所求,
∵点P1和点P关于OA对称,
∴OA垂直平分P1P.
又∵点M在AO上,
∴MP1=MP,同理可证PN=P2N,
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2=10
cm.
25.
解:(1)如图,连接B′B″.
作线段B'B″的垂直平分线EF.
则直线EF是△A′B′C′和△A″B″C″的对称轴.
(2)连接B′O.
∵△ABC和△A'B'C'关于直线MN对称,
∴∠BOM=∠B'OM.
又∵△A'B'C'和△A″B″C″关于直线EF对称,
∴∠B′OE=∠B″OE.
∴∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α
即∠BOB″=2α.
