沪科教 课标版_选修3-5_1.2探究动量守恒定律 课件23张PPT
文档属性
| 名称 | 沪科教 课标版_选修3-5_1.2探究动量守恒定律 课件23张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 1016.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-25 09:10:46 | ||
图片预览








文档简介
16.3 动量守恒定律
1、理解系统、内力、外力的概念。
2、知道动量守恒定律的表达式,理解其守恒的条件。
3、知道动量守恒定律的普遍意义及适用范围。
4、掌握运用动量守恒定律的一般步骤。
相关概念:
(1)系统:相互作用的 组成的整体。
(2)内力:系统 物体间的相互作用力。
(3)外力:系统 的物体对系统 的物体的作用力。
两个或多个物体
内部
以外
以内
(请自主阅读教材P12)
G1
G2
F1
F2
系统
内力
外力
A
B
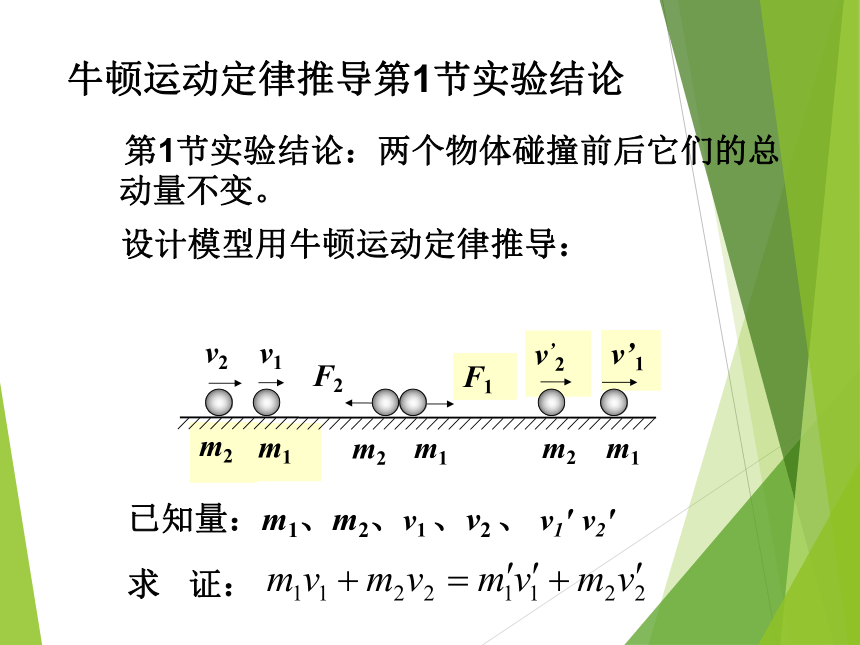
牛顿运动定律推导第1节实验结论
第1节实验结论:两个物体碰撞前后它们的总动量不变。
设计模型用牛顿运动定律推导:
v2
v1
v’2
v’1
m2
F1
F2
m1
m1
m2
m1
m2
已知量:m1、m2、v1 、v2 、 v1′ v2′
求 证:
推导过程
1、研究对象
2、受力分析
3、运动分析
4、建立方程
5、推导结论
过程详解
由牛顿第二定律,碰撞过程两球的加速度分别是
根据牛顿第三定律,它们大小相等,方向相反,
即 F1= -F2
碰撞时两球之间的作用力很短,用△t表示。
加速度和碰撞前后速度关系就是
过程详解
把加速度的表达代入 ,移项后得到
它的物理意义是:
两球碰撞之前的动量之和等于碰撞后的动量之和。
说明:
系统的动量在整个过程中一直不变。因此我们说这个过程中动量是守恒的。
动量守恒定律
内容:
如果一个系统不受外力,或者所受外力的矢量和等于0,这个系统的总动量不变。
表达式:
Δp1= -Δp2
动量守恒定律
注意:
在总动量一定的情况下,每个物体的动量
可以发生很大的变化。
四性:矢量、同时、相对、普适
动量守恒定律应用
在列车编组站里,一辆 m1 = 1.8×104 kg 的货车在平直轨道上以 v1 = 2 m/s 的速度运动,碰上一辆 m2 = 2.2×104 kg 的静止货车,它们碰撞后结合在一起继续运动,求货车碰撞后的运动速度。
v1
m2
m1
例题 1
分析:
1、研究对象
2、受力分析
3、过程分析
4、建立方程
5、求解方程
参考解答
解:取两辆货车在碰撞前运动方向为正方向,设两车接合后的速度为v, 则两车碰撞前的总动量为m1v1,碰撞后的总动量为(m1+m2)v,
由动量守恒定律可得:m1v1 = (m1+m2)v
m1
v1
m2
v2=0
初
m1+m2
v
末
正方向
动量守恒定律应用
例2
一枚在空中飞行的导弹,质量为 m ,在某点的速度为 v ,方向水平,如图所示。导弹在该点突然
炸裂成两块,其中质量为 m1 的
一块沿着与 v 相反的方向飞去,速度 v1 。求炸裂后另一块的速度 v2 。
分析:
1、研究对象
2、受力分析
3、过程分析
4、建立方程
5、求解方程
小结:上述两例属碰撞和爆炸过程,由于
对碰撞和爆炸过程的瞬间,其内力远大于
外力,所以在此过程系统的动量是守恒的
参考解答:
解 : 取炸裂前速度v的方向为正方向,根据动量守恒定律,可得 mv=(m-m1)v2 -m1v1
解得:
m
v
初
m1
v1
m-m1
v2
末
正方向
应用动量守恒定律解题“三步曲”
确定系统,判断动量是否守恒;
01
02
规定正方向,确定初、末动量;
03
根据动量守恒定律列式求解。
(2018年全国卷II理综试题)汽车A在水平冰雪路面上行驶,驾驶员发现其正前方停有汽车B,立即采取制动措施,但仍然撞上了汽车B。两车碰撞时和两车都完全停止后的位置如图所示,碰撞后B车向前滑动了4.5 m,A车向前滑动了2.0 m,已知A和B的质量分别为 kg和 kg,两车与该冰雪路面间的动摩擦因数均为0.10,两车碰撞时间极短,在碰撞后车轮均没有滚动,重力加速度大小 .求
(1)碰撞后的瞬间B车速度的大小;
(2)碰撞前的瞬间A车速度的大小。
聚焦高考考点
动量守恒定律的普适性
牛顿第二定律从“力”的角度反映物体间的相互作用。与过程中力的细节有关,只适应低速、宏观物体。
动量守恒定律从“动量”的角度描述物体间的相互作用。只涉及过程始末两个状态,与过程中力的细节无关。适应于目前为止物理学研究的一切领域。
动能定理从“能量”角度描述物体间的相互作用。只涉及过程始末两个状态。
一、动量守恒定律的内容及表达式:
二、动量守恒定律成立的条件:
如果一个系统不受外力或受外力的矢量和为零,这个系统的总动量保持不变。
1、不受力或者
2、
3、
三、应用动量守恒定律解决问题的基本步骤:
定系统,判条件
选方向,定状态
列方程,求结果
相互作用的两个物体组成的系统满足动量守恒,此时系统的能量是否也守恒?
1、理解系统、内力、外力的概念。
2、知道动量守恒定律的表达式,理解其守恒的条件。
3、知道动量守恒定律的普遍意义及适用范围。
4、掌握运用动量守恒定律的一般步骤。
相关概念:
(1)系统:相互作用的 组成的整体。
(2)内力:系统 物体间的相互作用力。
(3)外力:系统 的物体对系统 的物体的作用力。
两个或多个物体
内部
以外
以内
(请自主阅读教材P12)
G1
G2
F1
F2
系统
内力
外力
A
B
牛顿运动定律推导第1节实验结论
第1节实验结论:两个物体碰撞前后它们的总动量不变。
设计模型用牛顿运动定律推导:
v2
v1
v’2
v’1
m2
F1
F2
m1
m1
m2
m1
m2
已知量:m1、m2、v1 、v2 、 v1′ v2′
求 证:
推导过程
1、研究对象
2、受力分析
3、运动分析
4、建立方程
5、推导结论
过程详解
由牛顿第二定律,碰撞过程两球的加速度分别是
根据牛顿第三定律,它们大小相等,方向相反,
即 F1= -F2
碰撞时两球之间的作用力很短,用△t表示。
加速度和碰撞前后速度关系就是
过程详解
把加速度的表达代入 ,移项后得到
它的物理意义是:
两球碰撞之前的动量之和等于碰撞后的动量之和。
说明:
系统的动量在整个过程中一直不变。因此我们说这个过程中动量是守恒的。
动量守恒定律
内容:
如果一个系统不受外力,或者所受外力的矢量和等于0,这个系统的总动量不变。
表达式:
Δp1= -Δp2
动量守恒定律
注意:
在总动量一定的情况下,每个物体的动量
可以发生很大的变化。
四性:矢量、同时、相对、普适
动量守恒定律应用
在列车编组站里,一辆 m1 = 1.8×104 kg 的货车在平直轨道上以 v1 = 2 m/s 的速度运动,碰上一辆 m2 = 2.2×104 kg 的静止货车,它们碰撞后结合在一起继续运动,求货车碰撞后的运动速度。
v1
m2
m1
例题 1
分析:
1、研究对象
2、受力分析
3、过程分析
4、建立方程
5、求解方程
参考解答
解:取两辆货车在碰撞前运动方向为正方向,设两车接合后的速度为v, 则两车碰撞前的总动量为m1v1,碰撞后的总动量为(m1+m2)v,
由动量守恒定律可得:m1v1 = (m1+m2)v
m1
v1
m2
v2=0
初
m1+m2
v
末
正方向
动量守恒定律应用
例2
一枚在空中飞行的导弹,质量为 m ,在某点的速度为 v ,方向水平,如图所示。导弹在该点突然
炸裂成两块,其中质量为 m1 的
一块沿着与 v 相反的方向飞去,速度 v1 。求炸裂后另一块的速度 v2 。
分析:
1、研究对象
2、受力分析
3、过程分析
4、建立方程
5、求解方程
小结:上述两例属碰撞和爆炸过程,由于
对碰撞和爆炸过程的瞬间,其内力远大于
外力,所以在此过程系统的动量是守恒的
参考解答:
解 : 取炸裂前速度v的方向为正方向,根据动量守恒定律,可得 mv=(m-m1)v2 -m1v1
解得:
m
v
初
m1
v1
m-m1
v2
末
正方向
应用动量守恒定律解题“三步曲”
确定系统,判断动量是否守恒;
01
02
规定正方向,确定初、末动量;
03
根据动量守恒定律列式求解。
(2018年全国卷II理综试题)汽车A在水平冰雪路面上行驶,驾驶员发现其正前方停有汽车B,立即采取制动措施,但仍然撞上了汽车B。两车碰撞时和两车都完全停止后的位置如图所示,碰撞后B车向前滑动了4.5 m,A车向前滑动了2.0 m,已知A和B的质量分别为 kg和 kg,两车与该冰雪路面间的动摩擦因数均为0.10,两车碰撞时间极短,在碰撞后车轮均没有滚动,重力加速度大小 .求
(1)碰撞后的瞬间B车速度的大小;
(2)碰撞前的瞬间A车速度的大小。
聚焦高考考点
动量守恒定律的普适性
牛顿第二定律从“力”的角度反映物体间的相互作用。与过程中力的细节有关,只适应低速、宏观物体。
动量守恒定律从“动量”的角度描述物体间的相互作用。只涉及过程始末两个状态,与过程中力的细节无关。适应于目前为止物理学研究的一切领域。
动能定理从“能量”角度描述物体间的相互作用。只涉及过程始末两个状态。
一、动量守恒定律的内容及表达式:
二、动量守恒定律成立的条件:
如果一个系统不受外力或受外力的矢量和为零,这个系统的总动量保持不变。
1、不受力或者
2、
3、
三、应用动量守恒定律解决问题的基本步骤:
定系统,判条件
选方向,定状态
列方程,求结果
相互作用的两个物体组成的系统满足动量守恒,此时系统的能量是否也守恒?
同课章节目录
