沪科版数学九年级上册22.1比例线段 课件(共38张PPT)
文档属性
| 名称 | 沪科版数学九年级上册22.1比例线段 课件(共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 531.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 13:13:05 | ||
图片预览






文档简介
(共38张PPT)
比例线段
观察下面对应图片,你有什么发现?
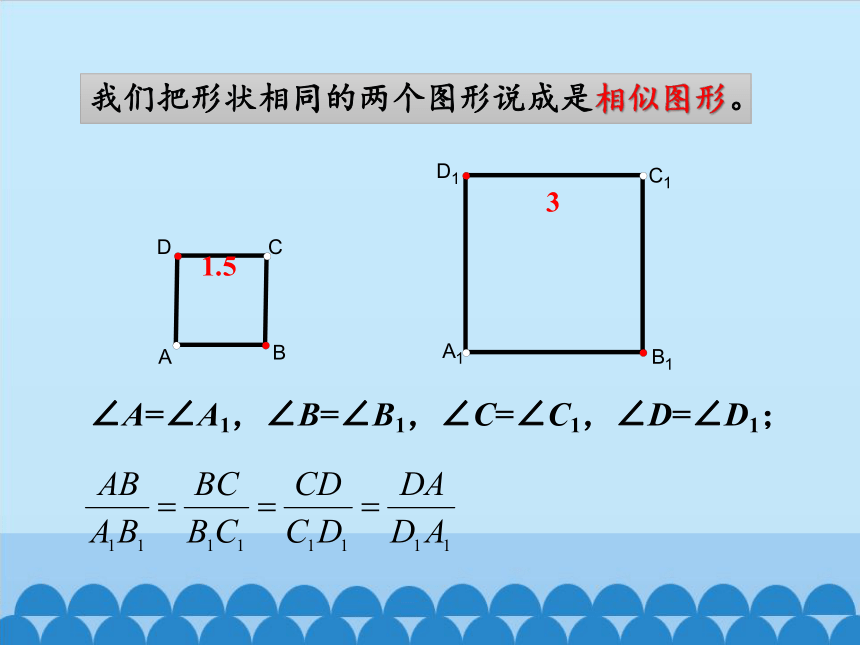
我们把形状相同的两个图形说成是相似图形。
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
1.5
3
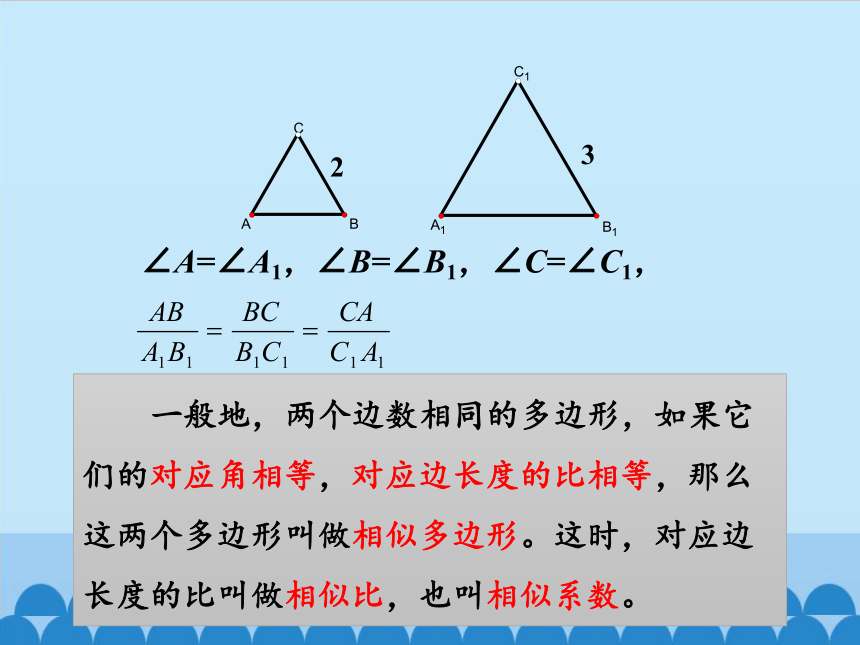
∠A=∠A1,∠B=∠B1,∠C=∠C1,
一般地,两个边数相同的多边形,如果它们的对应角相等,对应边长度的比相等,那么这两个多边形叫做相似多边形。这时,对应边长度的比叫做相似比,也叫相似系数。
2
3
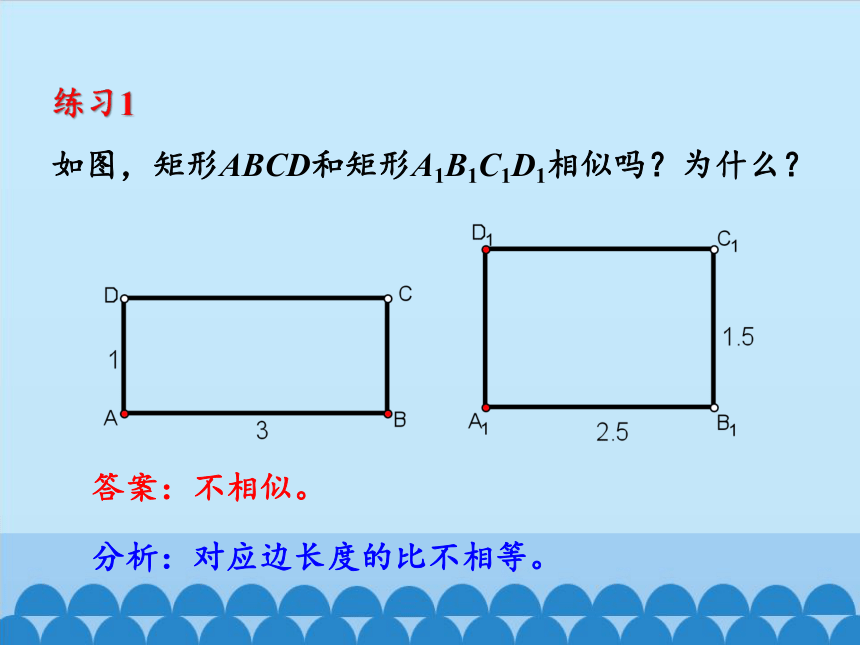
如图,矩形ABCD和矩形A1B1C1D1相似吗?为什么?
练习1
分析:对应边长度的比不相等。
答案:不相似。
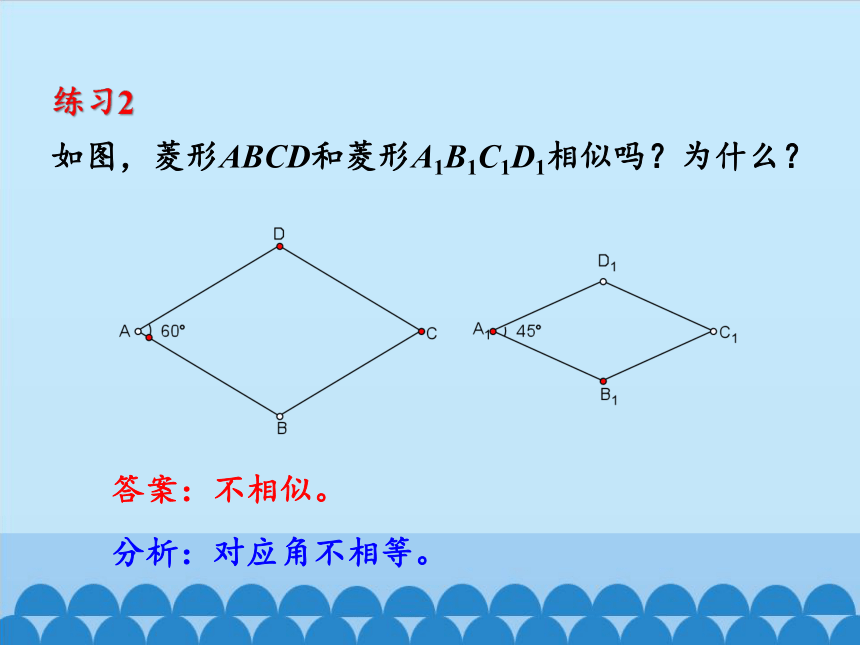
练习2
如图,菱形ABCD和菱形A1B1C1D1相似吗?为什么?
分析:对应角不相等。
答案:不相似。
做一做:
1.初三(1)班有男同学有30人,女同学20人,男同学和女同学的人数之比是多少?
2.一个长方形的长为6厘米,宽为4厘米,这个长方形的长与宽的比是多少?
定义:在同一长度单位下,两条线段的长度的比叫做这两条线段的比。
1.已知线段a=2cm,b=30mm,那么a,b两条线段的比是1∶15,对吗?为什么?
答:不对。根据定义,在同一长度单位下,两条线段的长度的比叫做这两条线段的比。
2.两线段的比值一定是正数吗?
答:两条线段的比值是一个没有单位的正数。
(1)两条线段的比就是它们的长度的比,求两线段的比时,长度单位必须统一,比与所选线段的长度单位无关,求比时,两条线段的长度单位要一致;
(2)两线段的比是一个没有单位的正数;
(3)两线段的比有顺序,除a=b外,a:b≠b:a,但a:b与b:a互为倒数;
(4)a:b=k说明a是b的k倍,这是线段的比的实质,两线段的比与选用的度量单位无关。
小结
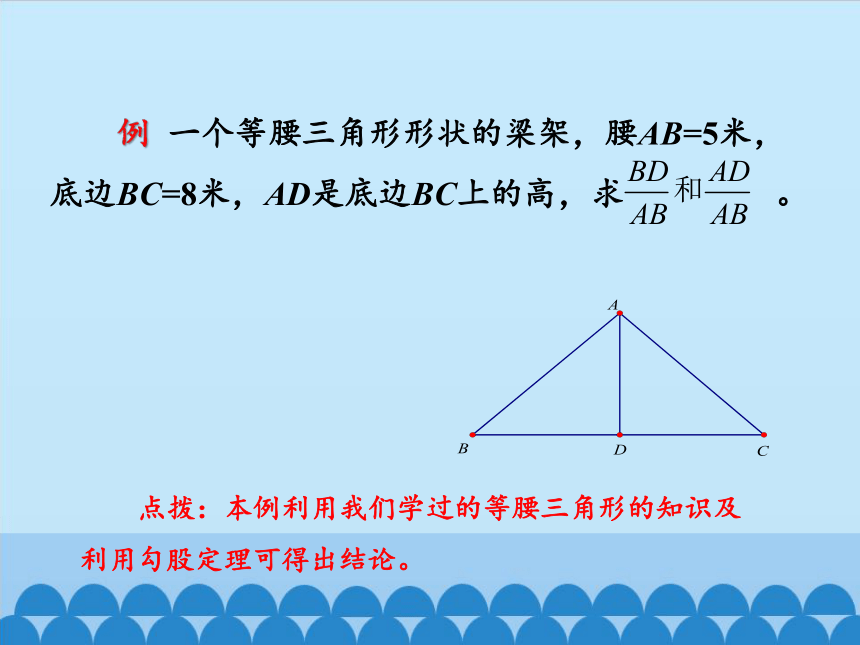
例
一个等腰三角形形状的梁架,腰AB=5米,底边BC=8米,AD是底边BC上的高,求
。
点拨:本例利用我们学过的等腰三角形的知识及利用勾股定理可得出结论。
求:图上距离与实际距离的比(即该地图的比例尺)?
实质就是求两线段的比,关键是单位统一,而且要注意两线段的顺序。
做一做
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段。
成比例线段的定义
相似多边形
比例线段
角:对应角相等
边:对应边长度的比相等
两条线段的比:
比例线段
①长度单位统一
②与单位无关,本身没有单位
③两条线段有顺序要求
①概念:项、比例内项、比例外项
②四条线段有顺序要求
③特别情况:比例中项
相似比(相似系数)
思考
(1)线段CD与HL、OA与OF、BE与GM的长度各是多少?
4
–1
–2
–3
1
2
3
5
1
x
y
2
3
4
5
6
O
A
B
C
D
E
(1)
–1
–2
–3
–4
–5
1
2
5
y
3
4
6
7
8
1
7
8
9
2
3
4
5
6
10
11
x
O
F
G
H
L
M
(2)
4
–1
–2
–3
1
2
3
5
1
x
y
2
3
4
5
6
O
A
B
C
D
E
(1)
–1
–2
–3
–4
–5
1
2
5
y
3
4
6
7
8
1
7
8
9
2
3
4
5
6
10
11
x
O
F
G
H
L
M
(2)
(2)如果每个点的横坐标、纵坐标都变成原来的2倍,如图(2),线段CD与HL的比、OA与OF的比、BE与GM的比各是多少?它们相等吗?
(3)在图中,你还能找到比相等的其它线段吗?
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即a/b=c/d,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段。
4
–1
–2
–3
1
2
3
5
1
x
y
2
3
4
5
6
O
A
B
C
D
E
(1)
–1
–2
–3
–4
–5
1
2
5
y
3
4
6
7
8
1
7
8
9
2
3
4
5
6
10
11
x
O
F
G
H
L
M
(2)
两条线段的比实际上就是两个数的比。
如果a,b,c,d四个数满足a/b=c/d,那么ad=bc吗?反过来,如果ad=bc,那么a/b=c/d吗?与同伴交流。
bd
bd
ad=bc
(2)ad=bc
ad
=bc
÷bd
÷bd
比例的基本性质
ad=bc
可以合写成:
比例的基本性质:
两内项之积等于两外项之积。
ad=bc;
(用“设k法”计算新比例)
例1
如图:
a
b
c
d
(1)
1
1
同理,
(2)
(3)
比例的合比性质
(1)
(2)
可以合写成:
特点:分母不变,分子加(或减)分母。
例2
已知:在下图中的ΔABC中,
。
求证:
比例的等比性质
学以致用──巧用比例性质解题
B
C
6
平行线分线段成比例定理
如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。
∴DE=EF
即AB、BC、DE、EF四条线段成比例。
∵l1∥l2∥l3,AB=BC
A
B
C
D
E
F
问:若AB≠BC即
,还有类似比例式成立吗?
新授
有AP1=P1B=BP2=P2P3=P3C
F
A
D
C
B
E
如图,l1∥l2∥l3,
问:
是否成立?
提问:运用比例性质,由
还可得到哪些比例式?
1.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
平移
B
A
C
A
B
F
E
C
D
M
(D)
E
F
平移
A
B
C
平移
A
B
C
E
D
N
F
D
F
(E)
注意:应用平行线分线段成比例定理得到的比例式中,四条线段与两直线的交点位置无关!
2.推论:平行于三角形一边的直线截其他两边(或两边延长线),截得的对应线段成比例。
A
C
B
F
E
A
F
E
C
B
3.三角形内角平分线定理:
三角形的内角平分线分对边所得的两条线段与这个角的两边对应成比例。
A
D
C
B
E
例1
已知:如图l1∥l2∥l3,AB=3,DE=2,EF=4。求BC。
解:因为l1∥l2∥l3
∴BC=6
(平行线分线段成比例定理)
E
F
D
B
A
C
证明:因为l1∥l2∥l3,
(平行线分线段成比例定理)
B
E
C
D
A
F
例2
如图l1∥l2∥l3,
,求证:
。
练习
E
B
A
D
C
F
1.已知:如图l1∥l2∥l3,求证:
。
小结
1.平行线分线段成比例定理(内容要理解);
2.定理的形象记忆法;
3.定理的变式图形;
4.定理的初步应用。
谢
谢
比例线段
观察下面对应图片,你有什么发现?
我们把形状相同的两个图形说成是相似图形。
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
1.5
3
∠A=∠A1,∠B=∠B1,∠C=∠C1,
一般地,两个边数相同的多边形,如果它们的对应角相等,对应边长度的比相等,那么这两个多边形叫做相似多边形。这时,对应边长度的比叫做相似比,也叫相似系数。
2
3
如图,矩形ABCD和矩形A1B1C1D1相似吗?为什么?
练习1
分析:对应边长度的比不相等。
答案:不相似。
练习2
如图,菱形ABCD和菱形A1B1C1D1相似吗?为什么?
分析:对应角不相等。
答案:不相似。
做一做:
1.初三(1)班有男同学有30人,女同学20人,男同学和女同学的人数之比是多少?
2.一个长方形的长为6厘米,宽为4厘米,这个长方形的长与宽的比是多少?
定义:在同一长度单位下,两条线段的长度的比叫做这两条线段的比。
1.已知线段a=2cm,b=30mm,那么a,b两条线段的比是1∶15,对吗?为什么?
答:不对。根据定义,在同一长度单位下,两条线段的长度的比叫做这两条线段的比。
2.两线段的比值一定是正数吗?
答:两条线段的比值是一个没有单位的正数。
(1)两条线段的比就是它们的长度的比,求两线段的比时,长度单位必须统一,比与所选线段的长度单位无关,求比时,两条线段的长度单位要一致;
(2)两线段的比是一个没有单位的正数;
(3)两线段的比有顺序,除a=b外,a:b≠b:a,但a:b与b:a互为倒数;
(4)a:b=k说明a是b的k倍,这是线段的比的实质,两线段的比与选用的度量单位无关。
小结
例
一个等腰三角形形状的梁架,腰AB=5米,底边BC=8米,AD是底边BC上的高,求
。
点拨:本例利用我们学过的等腰三角形的知识及利用勾股定理可得出结论。
求:图上距离与实际距离的比(即该地图的比例尺)?
实质就是求两线段的比,关键是单位统一,而且要注意两线段的顺序。
做一做
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段。
成比例线段的定义
相似多边形
比例线段
角:对应角相等
边:对应边长度的比相等
两条线段的比:
比例线段
①长度单位统一
②与单位无关,本身没有单位
③两条线段有顺序要求
①概念:项、比例内项、比例外项
②四条线段有顺序要求
③特别情况:比例中项
相似比(相似系数)
思考
(1)线段CD与HL、OA与OF、BE与GM的长度各是多少?
4
–1
–2
–3
1
2
3
5
1
x
y
2
3
4
5
6
O
A
B
C
D
E
(1)
–1
–2
–3
–4
–5
1
2
5
y
3
4
6
7
8
1
7
8
9
2
3
4
5
6
10
11
x
O
F
G
H
L
M
(2)
4
–1
–2
–3
1
2
3
5
1
x
y
2
3
4
5
6
O
A
B
C
D
E
(1)
–1
–2
–3
–4
–5
1
2
5
y
3
4
6
7
8
1
7
8
9
2
3
4
5
6
10
11
x
O
F
G
H
L
M
(2)
(2)如果每个点的横坐标、纵坐标都变成原来的2倍,如图(2),线段CD与HL的比、OA与OF的比、BE与GM的比各是多少?它们相等吗?
(3)在图中,你还能找到比相等的其它线段吗?
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即a/b=c/d,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段。
4
–1
–2
–3
1
2
3
5
1
x
y
2
3
4
5
6
O
A
B
C
D
E
(1)
–1
–2
–3
–4
–5
1
2
5
y
3
4
6
7
8
1
7
8
9
2
3
4
5
6
10
11
x
O
F
G
H
L
M
(2)
两条线段的比实际上就是两个数的比。
如果a,b,c,d四个数满足a/b=c/d,那么ad=bc吗?反过来,如果ad=bc,那么a/b=c/d吗?与同伴交流。
bd
bd
ad=bc
(2)ad=bc
ad
=bc
÷bd
÷bd
比例的基本性质
ad=bc
可以合写成:
比例的基本性质:
两内项之积等于两外项之积。
ad=bc;
(用“设k法”计算新比例)
例1
如图:
a
b
c
d
(1)
1
1
同理,
(2)
(3)
比例的合比性质
(1)
(2)
可以合写成:
特点:分母不变,分子加(或减)分母。
例2
已知:在下图中的ΔABC中,
。
求证:
比例的等比性质
学以致用──巧用比例性质解题
B
C
6
平行线分线段成比例定理
如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。
∴DE=EF
即AB、BC、DE、EF四条线段成比例。
∵l1∥l2∥l3,AB=BC
A
B
C
D
E
F
问:若AB≠BC即
,还有类似比例式成立吗?
新授
有AP1=P1B=BP2=P2P3=P3C
F
A
D
C
B
E
如图,l1∥l2∥l3,
问:
是否成立?
提问:运用比例性质,由
还可得到哪些比例式?
1.平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
平移
B
A
C
A
B
F
E
C
D
M
(D)
E
F
平移
A
B
C
平移
A
B
C
E
D
N
F
D
F
(E)
注意:应用平行线分线段成比例定理得到的比例式中,四条线段与两直线的交点位置无关!
2.推论:平行于三角形一边的直线截其他两边(或两边延长线),截得的对应线段成比例。
A
C
B
F
E
A
F
E
C
B
3.三角形内角平分线定理:
三角形的内角平分线分对边所得的两条线段与这个角的两边对应成比例。
A
D
C
B
E
例1
已知:如图l1∥l2∥l3,AB=3,DE=2,EF=4。求BC。
解:因为l1∥l2∥l3
∴BC=6
(平行线分线段成比例定理)
E
F
D
B
A
C
证明:因为l1∥l2∥l3,
(平行线分线段成比例定理)
B
E
C
D
A
F
例2
如图l1∥l2∥l3,
,求证:
。
练习
E
B
A
D
C
F
1.已知:如图l1∥l2∥l3,求证:
。
小结
1.平行线分线段成比例定理(内容要理解);
2.定理的形象记忆法;
3.定理的变式图形;
4.定理的初步应用。
谢
谢
