华东师大版九年级上册22.3实践与探索2.图形面积问题课件(共19张PPT)
文档属性
| 名称 | 华东师大版九年级上册22.3实践与探索2.图形面积问题课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 809.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 13:11:02 | ||
图片预览




文档简介
(共19张PPT)
22.3实践与探索
2、图形面积问题
华东师大版九年级上册
学而不疑则怠,疑而不探则空
列一元二次方程解应用题的一般步骤:
(1)审.弄清题意,明确已知量、未知量
及问题中的等量关系;
(2)设.根据具体问题可设直接和间接未知数;
(3)列.一般先找出能够表达应用题全部含
义的一个相等关系,列方程;
(4)解.选择适当的方法求出方程的解;
(5)验.检查求出来的未知数的值是否满足
方程、是否符合实际;
(6)答.按照题中的要求完整回答(注意单位)
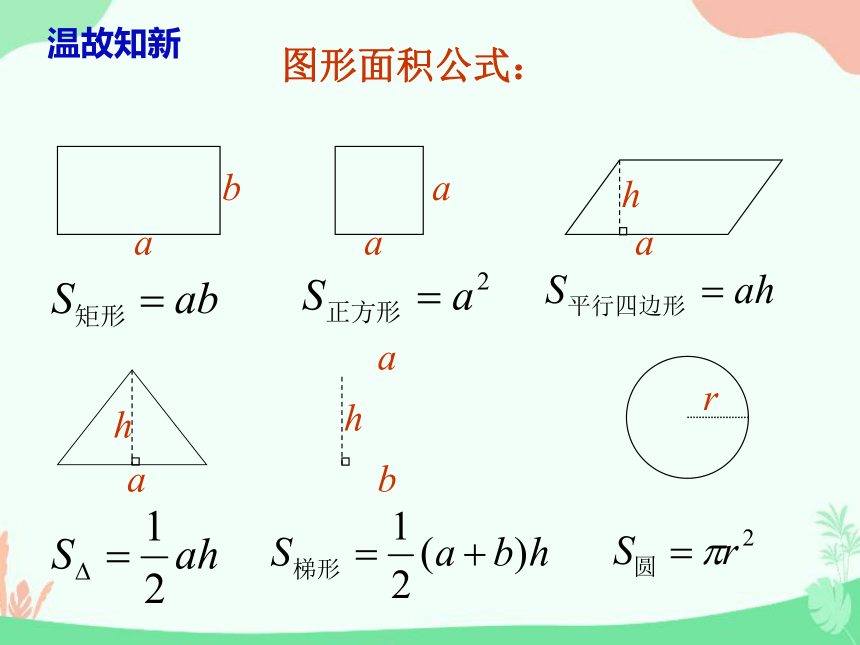
图形面积公式:
a
b
a
a
a
h
a
h
b
a
h
r
温故知新
某学校教学楼前有一块长30m、宽25m的
土地,准备建成花园.为了管理及观赏的方便,
准备沿平行于两边的方向纵、横各开辟一条等宽的小道,要满足花园面积为594m2,小道的宽应是多少?
例题解析1
30m
25m
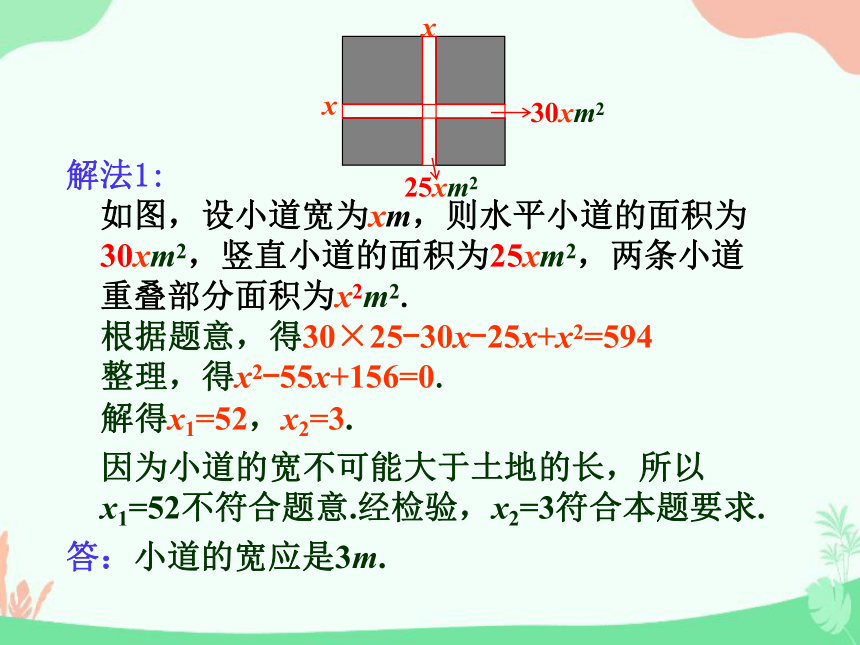
解法1:
如图,设小道宽为xm,则水平小道的面积为
30xm2,竖直小道的面积为25xm2,两条小道
重叠部分面积为x2m2.
根据题意,得30×25-30x-25x+x2=594
整理,得x2-55x+156=0.
解得x1=52,x2=3.
因为小道的宽不可能大于土地的长,所以x1=52不符合题意.经检验,x2=3符合本题要求.
答:小道的宽应是3m.
x
x
30xm2
25xm2
解法2:
假如把小道平移到两边(相当于
将四块花园平移成完整的一块).
如图,设小道宽为xm,则花园
的长为(30-x)m,宽为(25-x)m.
根据题意,得(30-x)(25-x)=594
注意:列方程解应用题时,要对所求出的未知数进行检验,检验的目的有两个:其一,检验求出来的未知数的值是否满足方程;其二,检验求出来的未知数的值是否满足实际问题的要求,对于适合方程而不适合实际问题的未知数的值应舍去。
整理,得x2-55x+156=0.
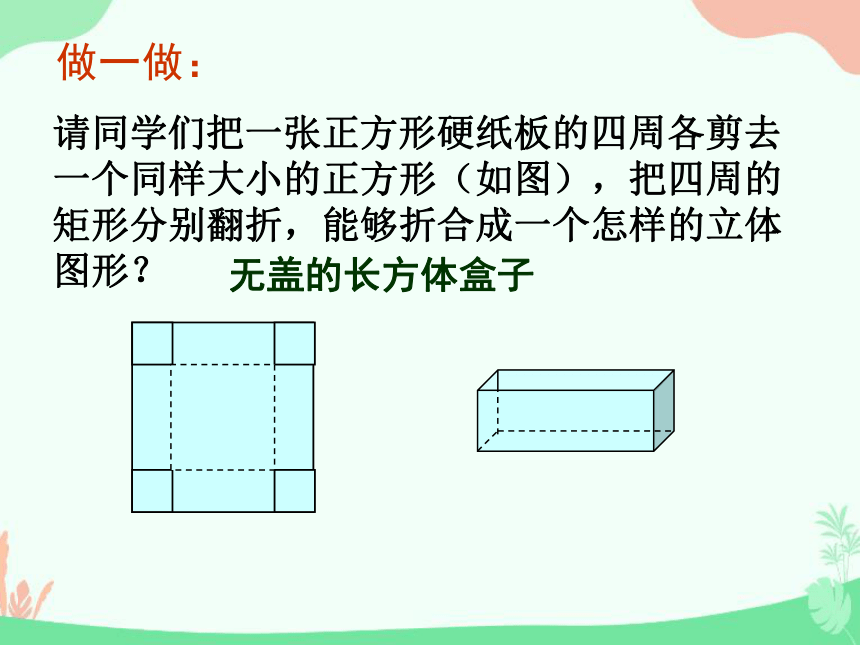
做一做:
请同学们把一张正方形硬纸板的四周各剪去一个同样大小的正方形(如图),把四周的矩形分别翻折,能够折合成一个怎样的立体图形?
无盖的长方体盒子
例题解析2
要制作一个容积为756cm2,高为
6cm,底面长比宽多5cm的无盖的长方体
铁盒,应选用多大尺寸的长方形铁片?
解:设长方体的底面宽为xcm,则长为(x+5)cm,
底面积为x(x+5)cm2.
根据题意,得6x(x+5)=756
整理,得
x2+5x-126=0.
解得x1=9,x2=-14.
因为x2=-14<0,不合题意,舍去.
故当x=9时,x+5+12=26,x+12=21.
答:应选用长为26cm,宽为21cm的长方形铁片。
x
x+5
6
6
6
6
6
6
6
6
x+5+12
x+12
将边长为10cm的正方形硬纸板的四周各剪去一个同样大小的正方形,再折叠成一个无盖的长方体盒子.
(1)如果要求长方体的底面面积为81cm2
,那么剪去的正方形边长为多少?
解:设剪去的小正方形边长为xcm,
则底面边长为(10-2x)cm.
根据题意,得(10-2x)2
=81
解方程,得x1=0.5,x2=9.5(不合题意,舍去)
答:剪去的小正方形边长0.5cm.
延伸探究
(2)如果按下表列出的长方体底面面积的数据要求,那么剪去的正方形边长会发生什么样的变化?折合成的长方体的侧面积又会发生什么样的变化?
(面积:cm2
边长:cm)
折合成的长
方体底面积
81
64
49
36
25
16
9
4
1
剪去的正方
形边长
折合成的长
方体侧面积
0.5
1
1.5
2
2.5
3
3.5
4
18
32
42
48
50
48
42
32
18
4.5
在你观察到的变化中,你感到折合而成的
长方体的侧面积会不会有最大的情况?
以剪去的正方形的边长为自变量,折合而成的长方体侧面积为函数,并在直角坐标系中画出相应的点.看看与你的感觉是否一致.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
x(cm)
y(cm2)
50
48
42
32
18
你能说明理由吗?
解:设剪去的小正方形边长为xcm,
侧面积为ycm,由矩形面积公式得
y
=
4·x·(10-2x)
=
-
8(x
-
2.5)2+50
故当x=2.5时,y有最大值为50
.
=
-
8x2
+40x
例题解析3
用一根长22厘米的铁丝,能否
折成一个面积是30厘米2的矩形?能否
折成一个面积为32厘米2的矩形?说明理由。
应用
学校准备在图书馆后面的场地边建一个面积
为50平方米的矩形自行车棚.一边利用图书馆
的后墙,并利用已有总长为25米的铁围栏.
请你设计如何搭建比较合适?
x
解:设与后墙平行的一边长为x米,则另两
边长之和为(25-x)米.
经检验,均符合题意.
x
答:与后墙平行的一边长为20米,另两边长都为2.5米;或与后墙平行的一边长为5米,另两边长都为10米.一般采用第一种方法,若后墙长不足20米,则采用第二种方法。
知识小结
本节课要掌握:
步骤为:审题、设元、列式、求解、检验、作答
如何列一元二次方程解图形面积类问题.
解决这类问题的关键是掌握常见几何图形
的面积体积公式,并能熟练计算由基本图
形构成的组合图形的面积.
课后作业
列一元二次方程解应用题:
1、如图,在一块长为92米,宽为60米的矩形耕地上挖水渠,东西和南北走向分别挖一条和两条水渠,水渠的宽都相等,而且要保证余下的可耕面积为5310平方米,水渠应挖多宽?
92米
60米
2、某大学为改善校园环境,计划在一块长80m,宽60m的矩形场地的中央建一矩形网球场.网球场占地面积为3500m2,四周为宽度相等的人行步道,求人行步道的宽度。
3、用一块长80cm,宽60cm的薄钢片,在四个角上分别截去相同的边长为xcm的小正方形,然后做成一个没有盖的长方体盒子.(1)若长方体盒子的底面积为1500cm2,你能求出小正方形的边长吗?(2)折合而成的长方体的侧面积会不会有最大的情况?若有,你能求出小正方形的边长吗?若没有请说明理由.
4、如图,有长为24米的篱笆,一面利用墙(墙的最大长度为11米),围成中间隔有一道篱笆的长方形花圃.(1)如果要围成面积为45平方米的花圃,那么AD的长为多少米?(2)能否围成面积为60平方米的花圃?若能,请求出AD的长;若不能,请说明理由。
A
B
C
D
22.3实践与探索
2、图形面积问题
华东师大版九年级上册
学而不疑则怠,疑而不探则空
列一元二次方程解应用题的一般步骤:
(1)审.弄清题意,明确已知量、未知量
及问题中的等量关系;
(2)设.根据具体问题可设直接和间接未知数;
(3)列.一般先找出能够表达应用题全部含
义的一个相等关系,列方程;
(4)解.选择适当的方法求出方程的解;
(5)验.检查求出来的未知数的值是否满足
方程、是否符合实际;
(6)答.按照题中的要求完整回答(注意单位)
图形面积公式:
a
b
a
a
a
h
a
h
b
a
h
r
温故知新
某学校教学楼前有一块长30m、宽25m的
土地,准备建成花园.为了管理及观赏的方便,
准备沿平行于两边的方向纵、横各开辟一条等宽的小道,要满足花园面积为594m2,小道的宽应是多少?
例题解析1
30m
25m
解法1:
如图,设小道宽为xm,则水平小道的面积为
30xm2,竖直小道的面积为25xm2,两条小道
重叠部分面积为x2m2.
根据题意,得30×25-30x-25x+x2=594
整理,得x2-55x+156=0.
解得x1=52,x2=3.
因为小道的宽不可能大于土地的长,所以x1=52不符合题意.经检验,x2=3符合本题要求.
答:小道的宽应是3m.
x
x
30xm2
25xm2
解法2:
假如把小道平移到两边(相当于
将四块花园平移成完整的一块).
如图,设小道宽为xm,则花园
的长为(30-x)m,宽为(25-x)m.
根据题意,得(30-x)(25-x)=594
注意:列方程解应用题时,要对所求出的未知数进行检验,检验的目的有两个:其一,检验求出来的未知数的值是否满足方程;其二,检验求出来的未知数的值是否满足实际问题的要求,对于适合方程而不适合实际问题的未知数的值应舍去。
整理,得x2-55x+156=0.
做一做:
请同学们把一张正方形硬纸板的四周各剪去一个同样大小的正方形(如图),把四周的矩形分别翻折,能够折合成一个怎样的立体图形?
无盖的长方体盒子
例题解析2
要制作一个容积为756cm2,高为
6cm,底面长比宽多5cm的无盖的长方体
铁盒,应选用多大尺寸的长方形铁片?
解:设长方体的底面宽为xcm,则长为(x+5)cm,
底面积为x(x+5)cm2.
根据题意,得6x(x+5)=756
整理,得
x2+5x-126=0.
解得x1=9,x2=-14.
因为x2=-14<0,不合题意,舍去.
故当x=9时,x+5+12=26,x+12=21.
答:应选用长为26cm,宽为21cm的长方形铁片。
x
x+5
6
6
6
6
6
6
6
6
x+5+12
x+12
将边长为10cm的正方形硬纸板的四周各剪去一个同样大小的正方形,再折叠成一个无盖的长方体盒子.
(1)如果要求长方体的底面面积为81cm2
,那么剪去的正方形边长为多少?
解:设剪去的小正方形边长为xcm,
则底面边长为(10-2x)cm.
根据题意,得(10-2x)2
=81
解方程,得x1=0.5,x2=9.5(不合题意,舍去)
答:剪去的小正方形边长0.5cm.
延伸探究
(2)如果按下表列出的长方体底面面积的数据要求,那么剪去的正方形边长会发生什么样的变化?折合成的长方体的侧面积又会发生什么样的变化?
(面积:cm2
边长:cm)
折合成的长
方体底面积
81
64
49
36
25
16
9
4
1
剪去的正方
形边长
折合成的长
方体侧面积
0.5
1
1.5
2
2.5
3
3.5
4
18
32
42
48
50
48
42
32
18
4.5
在你观察到的变化中,你感到折合而成的
长方体的侧面积会不会有最大的情况?
以剪去的正方形的边长为自变量,折合而成的长方体侧面积为函数,并在直角坐标系中画出相应的点.看看与你的感觉是否一致.
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
x(cm)
y(cm2)
50
48
42
32
18
你能说明理由吗?
解:设剪去的小正方形边长为xcm,
侧面积为ycm,由矩形面积公式得
y
=
4·x·(10-2x)
=
-
8(x
-
2.5)2+50
故当x=2.5时,y有最大值为50
.
=
-
8x2
+40x
例题解析3
用一根长22厘米的铁丝,能否
折成一个面积是30厘米2的矩形?能否
折成一个面积为32厘米2的矩形?说明理由。
应用
学校准备在图书馆后面的场地边建一个面积
为50平方米的矩形自行车棚.一边利用图书馆
的后墙,并利用已有总长为25米的铁围栏.
请你设计如何搭建比较合适?
x
解:设与后墙平行的一边长为x米,则另两
边长之和为(25-x)米.
经检验,均符合题意.
x
答:与后墙平行的一边长为20米,另两边长都为2.5米;或与后墙平行的一边长为5米,另两边长都为10米.一般采用第一种方法,若后墙长不足20米,则采用第二种方法。
知识小结
本节课要掌握:
步骤为:审题、设元、列式、求解、检验、作答
如何列一元二次方程解图形面积类问题.
解决这类问题的关键是掌握常见几何图形
的面积体积公式,并能熟练计算由基本图
形构成的组合图形的面积.
课后作业
列一元二次方程解应用题:
1、如图,在一块长为92米,宽为60米的矩形耕地上挖水渠,东西和南北走向分别挖一条和两条水渠,水渠的宽都相等,而且要保证余下的可耕面积为5310平方米,水渠应挖多宽?
92米
60米
2、某大学为改善校园环境,计划在一块长80m,宽60m的矩形场地的中央建一矩形网球场.网球场占地面积为3500m2,四周为宽度相等的人行步道,求人行步道的宽度。
3、用一块长80cm,宽60cm的薄钢片,在四个角上分别截去相同的边长为xcm的小正方形,然后做成一个没有盖的长方体盒子.(1)若长方体盒子的底面积为1500cm2,你能求出小正方形的边长吗?(2)折合而成的长方体的侧面积会不会有最大的情况?若有,你能求出小正方形的边长吗?若没有请说明理由.
4、如图,有长为24米的篱笆,一面利用墙(墙的最大长度为11米),围成中间隔有一道篱笆的长方形花圃.(1)如果要围成面积为45平方米的花圃,那么AD的长为多少米?(2)能否围成面积为60平方米的花圃?若能,请求出AD的长;若不能,请说明理由。
A
B
C
D
