人教版八年级上册数学课件:12.2.4两个直角三角形全等的判定条件(21张PPT)
文档属性
| 名称 | 人教版八年级上册数学课件:12.2.4两个直角三角形全等的判定条件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 788.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 11:44:56 | ||
图片预览






文档简介
(共22张PPT)
12.
2.
4
直角三角形全等的判定-斜边直角边
(HL)
一、教学目标????
?1.知识与技能?????在操作、比较中理解直角三角形全等的过程,并能用于解决实际问题.?????
2.过程与方法?????经历探索直角三角形全等判定的过程,掌握数学方法,提高合情推理的能力.????
?3.情感、态度与价值观?????培养几何推理意识,激发学生求知欲,感悟几何思维的内涵.?????
二、教学重、难点?????
1.重点:理解利用“斜边、直角边”来判定直角三角形全等的方
法.?????
2.难点:培养有条理的思考能力,正确使用“综合法”表达.?????
三、?教学过程?
1.你现在了解几种三角形的
全等判定方法
1.边边边
简称
“SSS”
2.两边及夹角
简称
“SAS”
3.两角及夹边
简称
“ASA”
4.两角及对边
简称
“AAS”
复习提问
2.
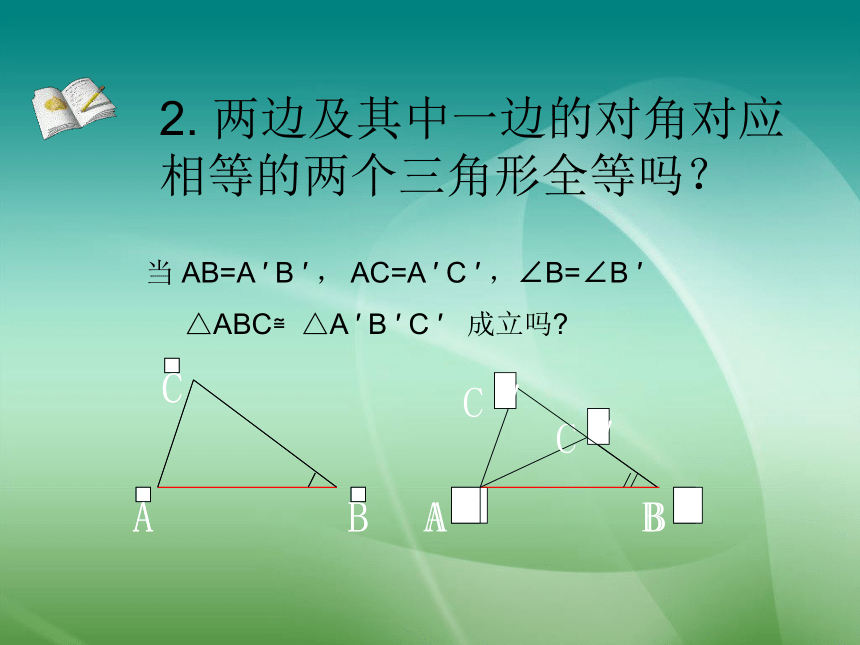
两边及其中一边的对角对应相等的两个三角形全等吗?
B
′
A
B
C
A
′
C
′
当
AB=A
′
B
′
,
AC=A
′
C
′
,∠B=∠B
′
△ABC≌△A
′
B
′
C
′
成立吗?
A
B
C
B
′
A
′
C
′
“边边角”分别对应相等是不能保证三角形全等的,那么当“角”为“直角”时“边边角”就成了“斜边直角边”,此时能否全等?
引入提问
动手做一做
1.随意画一个直角三角形ABC.
2.然后作另一个直角三角形,使它们的斜
边长度相等,一条直角边长度相等。
3.动手量量这两个三角形的边的长度和角
的度数,你有什么发现?
斜边和一条直角边对应相等的两个直角三角形全等.
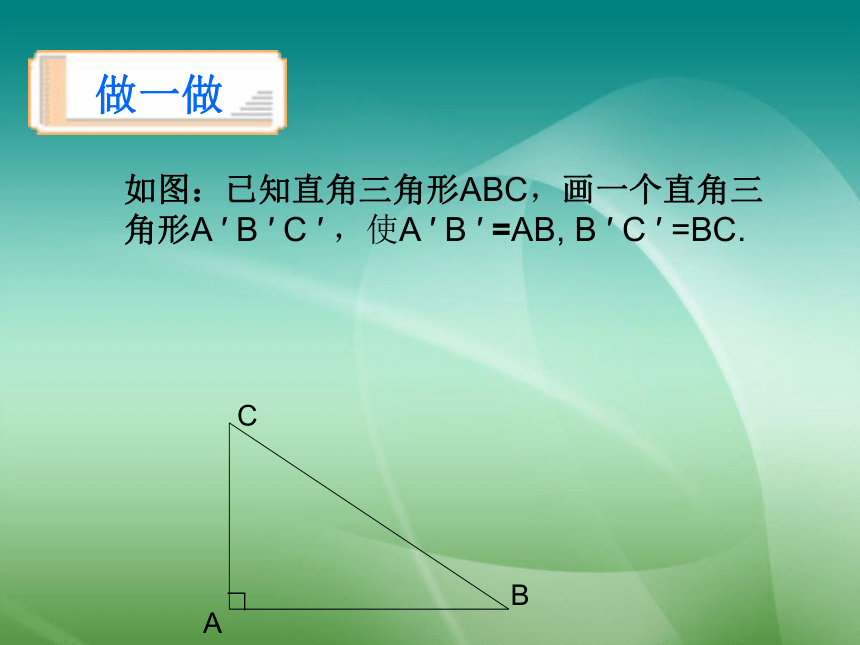
做一做
如图:已知直角三角形ABC,画一个直角三角形A
′
B
′
C
′
,使A
′
B
′
=AB,
B
′
C
′
=BC.
C
B
A
∟
做一做
步骤1:画一线段AB,使A
′
B
′
=AB;
A
′
B
′
步骤2:画∠MA′B′
=90°;
M
步骤3:以点B′为圆心以BC长为半径画圆弧,交射线A′M于点C′
;连结B′C′
。
C
′
如图△
A
′
B
′
C
′即为所求
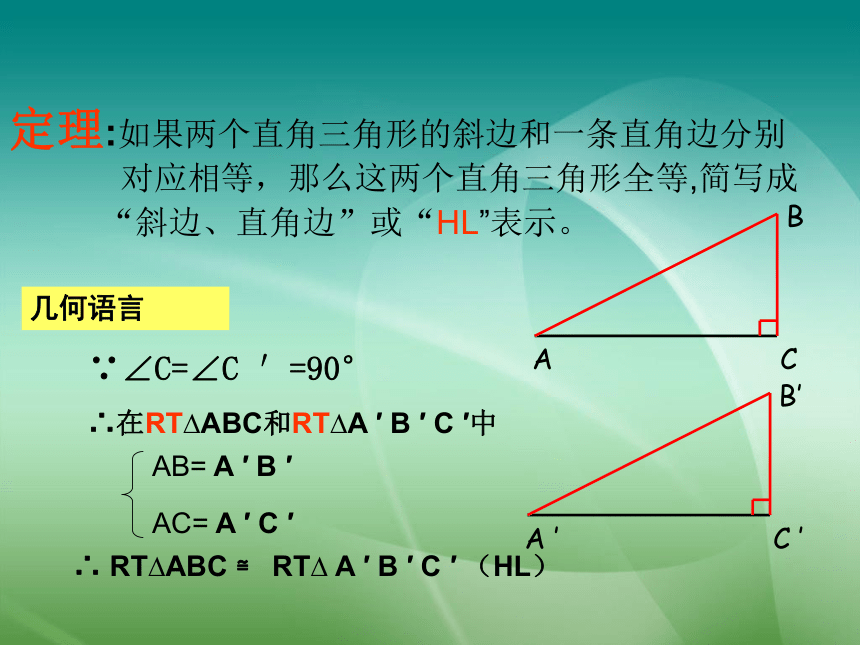
定理:如果两个直角三角形的斜边和一条直角边分别
对应相等,那么这两个直角三角形全等,简写成
“斜边、直角边”或“HL”表示。
∵∠C=∠C
′=90°
AB=
A
′
B
′
AC=
A
′
C
′
∴
RT?ABC
≌
RT?
A
′
B
′
C
′
(HL)
几何语言
∴在RT?ABC和RT?A
′
B
′
C
′中
A
B
C
A
′
B′
C
′
例5:
如图:已知AC=BD,∠C=
∠D=90°,求证Rt?ABC
≌Rt
?BAD
A
B
D
C
证明:∵∠C=∠D=90°
∴
?ABC
与?BAD都是直角三角形。
在Rt?ABC
与Rt
?BAD中
∴Rt?ABC
≌Rt
?BAD(HL)
AB=BA,
AC=BD,
例:
“三月三,放风筝”,
如图是小明制作的风筝,他用量角器测得∠B=∠D=90°,并且侧得BC=CD,不用再测量,他就知道AB=AD,请你用所学知识加以说明。
A
B
C
D
证明:∵∠B=∠D=90°
∴
?ABC
与?ADC都是直角三角形。
在Rt?ABC
与Rt
?ADC中
∴Rt?ABC
≌Rt
?ADC(HL)
∴AB=AD
BC=DC
AC=CA
练习快速回答问题
1.两个锐角对应相等的两个直角三角形全等吗?
2.两条直角边对应相等的两个直角三角形全等吗?
3.有任意的两条边对应相等的两个直角三角形全等吗?
4.有两边及一条边对应的三角形全等吗?
5.判定两个三角形全等,共有多少种方法?
练习
1、如图,在△ABC中,BD=CD,DE⊥AB,
DF⊥AC,E、F为垂足,DE=DF,
求证:△BED≌
△CFD
A
B
C
D
E
F
证明:∵DE⊥AB,DF⊥AC
∴∠DEB=∠DFC=90°
∴△DEB和△DFC是直角三角形
在Rt
△DEB和Rt
△DFC中
DB=CD
DE=DF
∴Rt
△DEB≌Rt
△DFC
∟
∟
练习
2、如图,AC=AD,∠C=∠D=90°
,
求证:BC=BD
A
B
C
D
证明:∵∠C=∠D=90°
∴△ABC和△ABD是直角三角形
在Rt
△ABC和Rt
△ABD中
AB=AB
AC=AD
∴Rt
△ABC≌Rt
△ABD
∴BC=BD
练习
如图已知CE⊥AB,DF⊥AB,AC=BD,AF=BE,则CE=DF。请说明理由。
A
B
C
D
E
F
练习
如图,AD是△ABC的高,E为AC上一定,BE交AD于F,且有BF=AC,FD=CD,试探索BE与AC的位置关系。
练习
如图,AB与CD相交与点O,由O作OE⊥AD,垂足为E,OF⊥BC,垂足为F。若AE=BF,AO=BO.求证:CO=DO
练习
已知,如图所示,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B,C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
小结:
1、应用斜边直角边(HL)公理判定两个三
角形全等,要按照公理的条件,准确地
找出“对应相等”的边和角;
2、寻找使结论成立所需要的条件时,要注
意充分利用图形中的隐含条件,如“公
共边、公共角、对顶角等等”;
3、要认真掌握证明两个三角形全等的推理
模式。
作业:
课本P43 练习第2题、
P44
习题第7题.
再见!
12.
2.
4
直角三角形全等的判定-斜边直角边
(HL)
一、教学目标????
?1.知识与技能?????在操作、比较中理解直角三角形全等的过程,并能用于解决实际问题.?????
2.过程与方法?????经历探索直角三角形全等判定的过程,掌握数学方法,提高合情推理的能力.????
?3.情感、态度与价值观?????培养几何推理意识,激发学生求知欲,感悟几何思维的内涵.?????
二、教学重、难点?????
1.重点:理解利用“斜边、直角边”来判定直角三角形全等的方
法.?????
2.难点:培养有条理的思考能力,正确使用“综合法”表达.?????
三、?教学过程?
1.你现在了解几种三角形的
全等判定方法
1.边边边
简称
“SSS”
2.两边及夹角
简称
“SAS”
3.两角及夹边
简称
“ASA”
4.两角及对边
简称
“AAS”
复习提问
2.
两边及其中一边的对角对应相等的两个三角形全等吗?
B
′
A
B
C
A
′
C
′
当
AB=A
′
B
′
,
AC=A
′
C
′
,∠B=∠B
′
△ABC≌△A
′
B
′
C
′
成立吗?
A
B
C
B
′
A
′
C
′
“边边角”分别对应相等是不能保证三角形全等的,那么当“角”为“直角”时“边边角”就成了“斜边直角边”,此时能否全等?
引入提问
动手做一做
1.随意画一个直角三角形ABC.
2.然后作另一个直角三角形,使它们的斜
边长度相等,一条直角边长度相等。
3.动手量量这两个三角形的边的长度和角
的度数,你有什么发现?
斜边和一条直角边对应相等的两个直角三角形全等.
做一做
如图:已知直角三角形ABC,画一个直角三角形A
′
B
′
C
′
,使A
′
B
′
=AB,
B
′
C
′
=BC.
C
B
A
∟
做一做
步骤1:画一线段AB,使A
′
B
′
=AB;
A
′
B
′
步骤2:画∠MA′B′
=90°;
M
步骤3:以点B′为圆心以BC长为半径画圆弧,交射线A′M于点C′
;连结B′C′
。
C
′
如图△
A
′
B
′
C
′即为所求
定理:如果两个直角三角形的斜边和一条直角边分别
对应相等,那么这两个直角三角形全等,简写成
“斜边、直角边”或“HL”表示。
∵∠C=∠C
′=90°
AB=
A
′
B
′
AC=
A
′
C
′
∴
RT?ABC
≌
RT?
A
′
B
′
C
′
(HL)
几何语言
∴在RT?ABC和RT?A
′
B
′
C
′中
A
B
C
A
′
B′
C
′
例5:
如图:已知AC=BD,∠C=
∠D=90°,求证Rt?ABC
≌Rt
?BAD
A
B
D
C
证明:∵∠C=∠D=90°
∴
?ABC
与?BAD都是直角三角形。
在Rt?ABC
与Rt
?BAD中
∴Rt?ABC
≌Rt
?BAD(HL)
AB=BA,
AC=BD,
例:
“三月三,放风筝”,
如图是小明制作的风筝,他用量角器测得∠B=∠D=90°,并且侧得BC=CD,不用再测量,他就知道AB=AD,请你用所学知识加以说明。
A
B
C
D
证明:∵∠B=∠D=90°
∴
?ABC
与?ADC都是直角三角形。
在Rt?ABC
与Rt
?ADC中
∴Rt?ABC
≌Rt
?ADC(HL)
∴AB=AD
BC=DC
AC=CA
练习快速回答问题
1.两个锐角对应相等的两个直角三角形全等吗?
2.两条直角边对应相等的两个直角三角形全等吗?
3.有任意的两条边对应相等的两个直角三角形全等吗?
4.有两边及一条边对应的三角形全等吗?
5.判定两个三角形全等,共有多少种方法?
练习
1、如图,在△ABC中,BD=CD,DE⊥AB,
DF⊥AC,E、F为垂足,DE=DF,
求证:△BED≌
△CFD
A
B
C
D
E
F
证明:∵DE⊥AB,DF⊥AC
∴∠DEB=∠DFC=90°
∴△DEB和△DFC是直角三角形
在Rt
△DEB和Rt
△DFC中
DB=CD
DE=DF
∴Rt
△DEB≌Rt
△DFC
∟
∟
练习
2、如图,AC=AD,∠C=∠D=90°
,
求证:BC=BD
A
B
C
D
证明:∵∠C=∠D=90°
∴△ABC和△ABD是直角三角形
在Rt
△ABC和Rt
△ABD中
AB=AB
AC=AD
∴Rt
△ABC≌Rt
△ABD
∴BC=BD
练习
如图已知CE⊥AB,DF⊥AB,AC=BD,AF=BE,则CE=DF。请说明理由。
A
B
C
D
E
F
练习
如图,AD是△ABC的高,E为AC上一定,BE交AD于F,且有BF=AC,FD=CD,试探索BE与AC的位置关系。
练习
如图,AB与CD相交与点O,由O作OE⊥AD,垂足为E,OF⊥BC,垂足为F。若AE=BF,AO=BO.求证:CO=DO
练习
已知,如图所示,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B,C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.
小结:
1、应用斜边直角边(HL)公理判定两个三
角形全等,要按照公理的条件,准确地
找出“对应相等”的边和角;
2、寻找使结论成立所需要的条件时,要注
意充分利用图形中的隐含条件,如“公
共边、公共角、对顶角等等”;
3、要认真掌握证明两个三角形全等的推理
模式。
作业:
课本P43 练习第2题、
P44
习题第7题.
再见!
