2020年秋苏科版九年级数学上册随堂练——2.4圆周角提升练习(word 版 含解析)
文档属性
| 名称 | 2020年秋苏科版九年级数学上册随堂练——2.4圆周角提升练习(word 版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 505.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 00:00:00 | ||
图片预览

文档简介
2.4圆周角提升练习
一、选择题
1.圆内接平行四边形是(
)
A.矩形
B.菱形
C.正方形
D.平行四边形
2.如图,A,B,C,D四个点均在⊙O上,若∠AOD=70°,AO∥DC,则∠B的度数为( )
A.40°
B.45°
C.50°
D.55°
3.如图,AB是半圆的直径,D是的中点,∠ABC=50°,则∠DAB等于( )
A.55°
B.60°
C.65°
D.70°
4.如图,点A,B,C都在⊙O上,且点C在弦AB所对的优弧上.如果∠AOB=64°,那么∠ACB的度数是( )
A.26°
B.30°
C.32°
D.64°
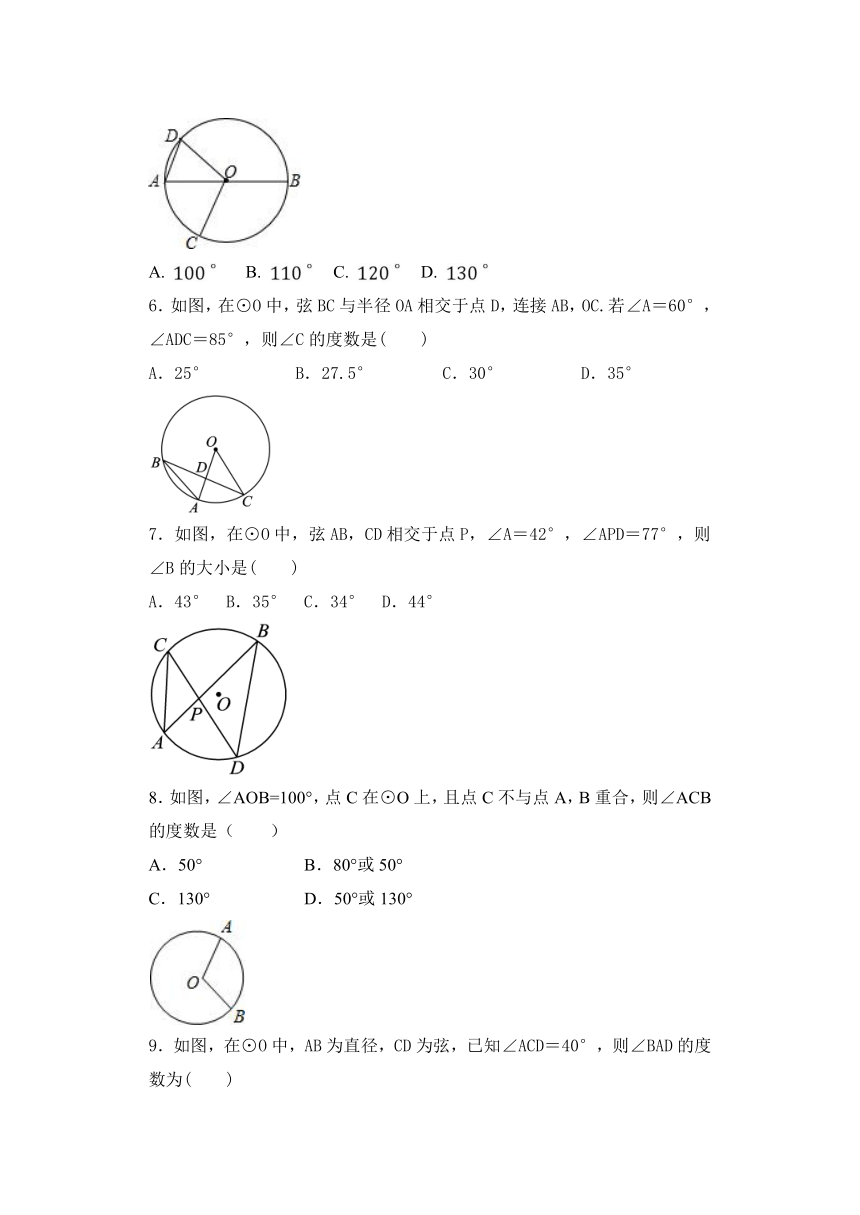
5.如图,AB是的直径,点C、D在上,,则
A.
B.
C.
D.
6.如图,在⊙O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是( )
A.25°
B.27.5°
C.30°
D.35°
7.如图,在⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
A.43°
B.35°
C.34°
D.44°
8.如图,∠AOB=100°,点C在⊙O上,且点C不与点A,B重合,则∠ACB的度数是(
)
A.50°
B.80°或50°
C.130°
D.50°或130°
9.如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD的度数为( )
A.50°
B.40°
C.45°
D.60°
二、填空题
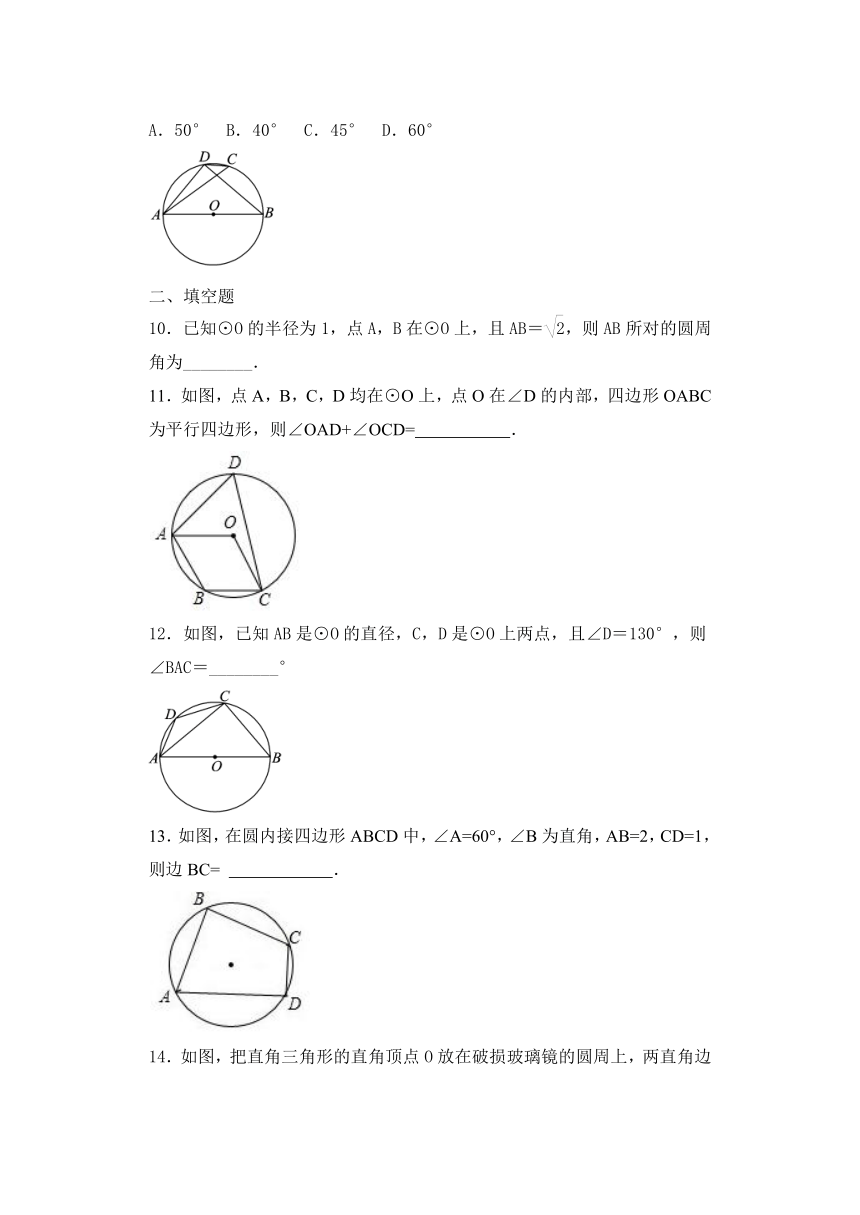
10.已知⊙O的半径为1,点A,B在⊙O上,且AB=,则AB所对的圆周角为________.
11.如图,点A,B,C,D均在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
.
12.如图,已知AB是⊙O的直径,C,D是⊙O上两点,且∠D=130°,则∠BAC=________°
13.如图,在圆内接四边形ABCD中,∠A=60°,∠B为直角,AB=2,CD=1,则边BC=
.
14.如图,把直角三角形的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8
cm,ON=6
cm,则该圆形玻璃镜的半径是
。
15.如图,已知平行四边形ABCD的顶点A.D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=
.
16.如图,已知AM是⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=
∠CAM,线段AB和AC分别交⊙O于点D,E.若∠BMD=40°,则∠EOM=________°.
17.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为____.
18.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.点E在上,则∠E=________°
三、解答题
19.如图,P是⊙O外的一点,C是⊙O上的一点.求证:∠ACB>∠APB.
20.如图,△ABC的高AD,BE相交于点H,延长AD交△ABC的外接圆于点G,连接BG.求证:HD=GD.
21.如图,AB为⊙O的直径,点C在⊙O上,连接BC并延长至点D,使CD=BC,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长.
答案
1.
A
2.
D
3.
C
4.
C
5.
C
6.
D
7.
B
8.
D
9.
A
10.
45°或135°
11.
60°
12.
40°
13.
14.
5cm
15.
58°
16.
80°
17.
110
18.
125°
19.
证明:如图,连接AN.
∵∠ANB=∠APB+∠NAP,
∴∠ANB>∠APB.
又∵∠ANB=∠ACB,∴∠ACB>∠APB.
20.
证明:∵∠C=∠G,AD,BE为△ABC的高,
∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,
∴∠C=∠AHE.
∵∠AHE=∠BHG,∴∠BHG=∠C,
∴∠G=∠BHG,
∴BH=BG.
又∵AD⊥BC,
∴HD=GD.
21.
(2)
一、选择题
1.圆内接平行四边形是(
)
A.矩形
B.菱形
C.正方形
D.平行四边形
2.如图,A,B,C,D四个点均在⊙O上,若∠AOD=70°,AO∥DC,则∠B的度数为( )
A.40°
B.45°
C.50°
D.55°
3.如图,AB是半圆的直径,D是的中点,∠ABC=50°,则∠DAB等于( )
A.55°
B.60°
C.65°
D.70°
4.如图,点A,B,C都在⊙O上,且点C在弦AB所对的优弧上.如果∠AOB=64°,那么∠ACB的度数是( )
A.26°
B.30°
C.32°
D.64°
5.如图,AB是的直径,点C、D在上,,则
A.
B.
C.
D.
6.如图,在⊙O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是( )
A.25°
B.27.5°
C.30°
D.35°
7.如图,在⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的大小是( )
A.43°
B.35°
C.34°
D.44°
8.如图,∠AOB=100°,点C在⊙O上,且点C不与点A,B重合,则∠ACB的度数是(
)
A.50°
B.80°或50°
C.130°
D.50°或130°
9.如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD的度数为( )
A.50°
B.40°
C.45°
D.60°
二、填空题
10.已知⊙O的半径为1,点A,B在⊙O上,且AB=,则AB所对的圆周角为________.
11.如图,点A,B,C,D均在⊙O上,点O在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
.
12.如图,已知AB是⊙O的直径,C,D是⊙O上两点,且∠D=130°,则∠BAC=________°
13.如图,在圆内接四边形ABCD中,∠A=60°,∠B为直角,AB=2,CD=1,则边BC=
.
14.如图,把直角三角形的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8
cm,ON=6
cm,则该圆形玻璃镜的半径是
。
15.如图,已知平行四边形ABCD的顶点A.D、C在⊙O上,顶点B在⊙O的直径AE上,连接DE,若∠E=32°,则∠C=
.
16.如图,已知AM是⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=
∠CAM,线段AB和AC分别交⊙O于点D,E.若∠BMD=40°,则∠EOM=________°.
17.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为____.
18.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.点E在上,则∠E=________°
三、解答题
19.如图,P是⊙O外的一点,C是⊙O上的一点.求证:∠ACB>∠APB.
20.如图,△ABC的高AD,BE相交于点H,延长AD交△ABC的外接圆于点G,连接BG.求证:HD=GD.
21.如图,AB为⊙O的直径,点C在⊙O上,连接BC并延长至点D,使CD=BC,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长.
答案
1.
A
2.
D
3.
C
4.
C
5.
C
6.
D
7.
B
8.
D
9.
A
10.
45°或135°
11.
60°
12.
40°
13.
14.
5cm
15.
58°
16.
80°
17.
110
18.
125°
19.
证明:如图,连接AN.
∵∠ANB=∠APB+∠NAP,
∴∠ANB>∠APB.
又∵∠ANB=∠ACB,∴∠ACB>∠APB.
20.
证明:∵∠C=∠G,AD,BE为△ABC的高,
∴∠C+∠DAC=90°,∠AHE+∠DAC=90°,
∴∠C=∠AHE.
∵∠AHE=∠BHG,∴∠BHG=∠C,
∴∠G=∠BHG,
∴BH=BG.
又∵AD⊥BC,
∴HD=GD.
21.
(2)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
