2020年秋苏科版九年级数学上册随堂练——2.6正多边形与圆提升练习(word 版 含答案)
文档属性
| 名称 | 2020年秋苏科版九年级数学上册随堂练——2.6正多边形与圆提升练习(word 版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 08:24:01 | ||
图片预览

文档简介
2.6正多边形与圆提升练习
一、选择题
1.已知正六边形的边心距为,则该正六边形的边长是(
)
A.
B.2
C.3
D.
2.如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列说法错误的是(
)
A.四边形EDCN是菱形
B.四边形MNCD是梯形
C.△AEM与△CBN均为等腰三角形
D.△EAN≌△EDM
3.有一个边长为50cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为(
)
A.50cm
B.
C,
D.
4.已知一个圆的半径为5
cm,则它的内接正六边形的边长为(
)
A.4
cm
B.5
cm
C.5.5
cm
D.6
cm
5.半径为a的正六边形的面积等于
A.
B.
C.
D.
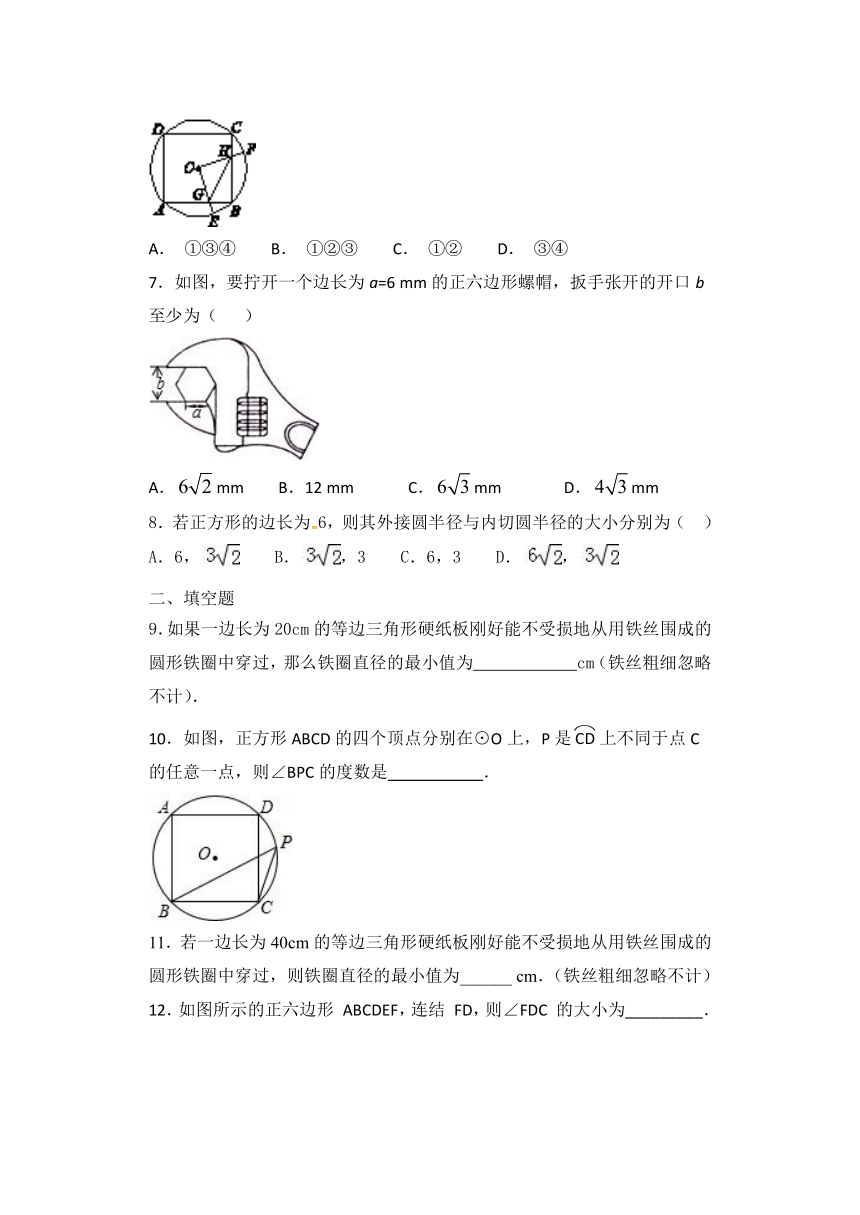
6.如图,边长为4的正方形ABCD内接于⊙O,E是弧AB上的一动点(不与A,B重合),F是弧BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①=;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+.其中正确的是( )
A.
①③④
B.
①②③
C.
①②
D.
③④
7.如图,要拧开一个边长为a=6
mm的正六边形螺帽,扳手张开的开口b至少为(
)
A.mm
B.12
mm
C.mm
D.mm
8.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为(
)
A.6,
B.,3
C.6,3
D.,
二、填空题
9.如果一边长为20cm的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过,那么铁圈直径的最小值为
cm(铁丝粗细忽略不计).
10.如图,正方形ABCD的四个顶点分别在⊙O上,P是上不同于点C的任意一点,则∠BPC的度数是
.
11.若一边长为40cm的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过,则铁圈直径的最小值为______
cm.(铁丝粗细忽略不计)
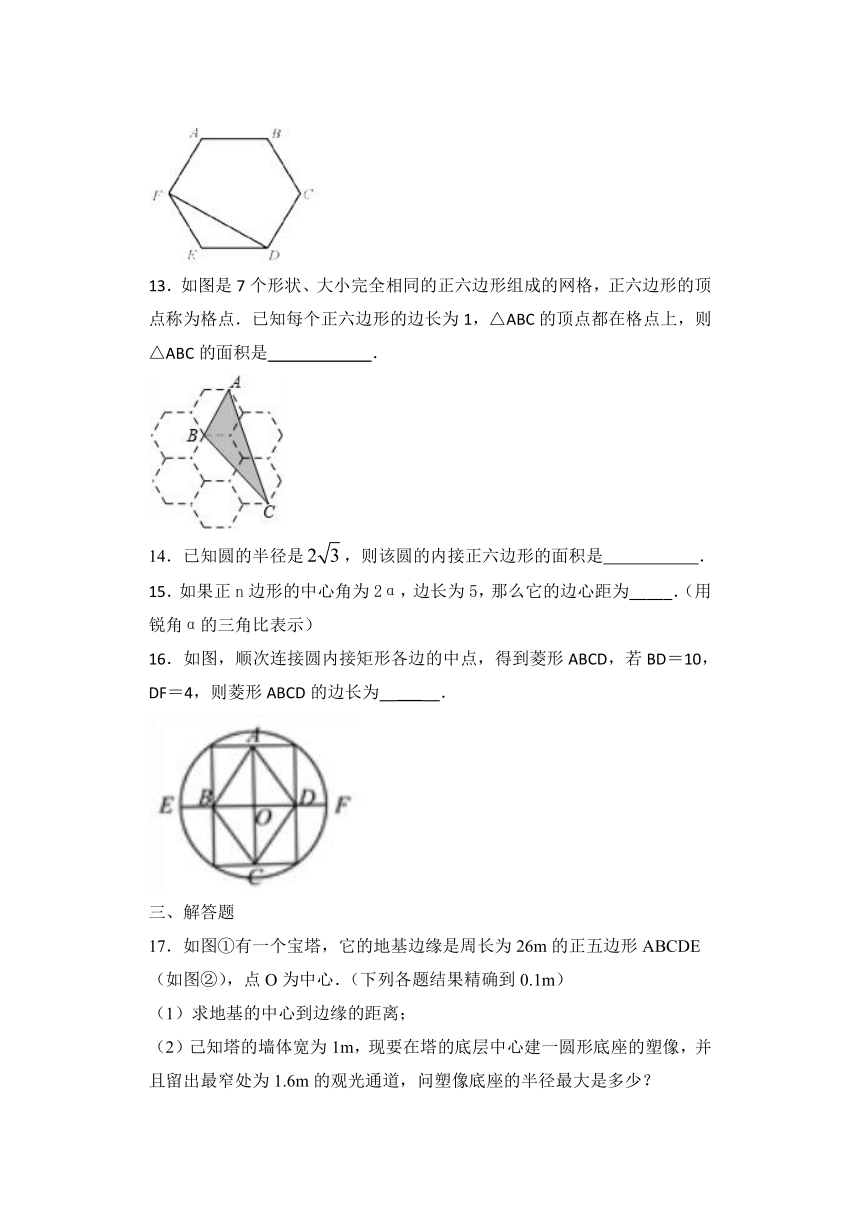
12.如图所示的正六边形
ABCDEF,连结
FD,则∠FDC
的大小为_________.
13.如图是7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是
.
14.已知圆的半径是,则该圆的内接正六边形的面积是
.
15.如果正n边形的中心角为2α,边长为5,那么它的边心距为_____.(用锐角α的三角比表示)
16.如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为__
__.
三、解答题
17.如图①有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心.(下列各题结果精确到0.1m)
(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?
18.如图,在的内接四边形ABCD中,,点E在上
求的度数;
连接OD、OE,当时,AE恰好为的内接正n边形的一边,求n的值.
19.(1)如图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点,且BM=CN,连接OM,ON,求∠MON的度数。
(2)图②、③、……
④中,M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、……正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON;则图②中∠MON的度数是__________,图③中∠MON的度数是__________;……由此可猜测在n边形图中∠MON的度数是_______
20.如图,已知正六边形ABCDEF,其外接圆的半径是a,求正六边形的周长和面积.
求⊙O的半径.
答案
1.
B
2.
D
3.
C
4.
B
5.
B
6.
C
7.
C
8.
B
9.
10.
45°
11.
12.
90°
13.
14.
15.
(或)
16.
9
17.
(1)作OM⊥AB于点M,连接OA、OB,则OM为边心距,∠AOB是中心角.
由正五边形性质得∠AOB=360°÷5=72°.
又AB=×26=5.2,
∴AM=2.6,∠AOM=36°,
在Rt△AMO中,边心距OM=
(2)3.6-1-1.6=1(m).
答:地基的中心到边缘的距离约为3.6m,塑像底座的半径最大约为1m.
18.
解:连接BD,
四边形ABCD是的内接四边形,
,,
,,
是等边三角形,,
四边形ABDE是的内接四边形,
,;
连接OA,
,
,
,
,
.??
19.
(1)120°
(2)90°、72°、°
20.
一、选择题
1.已知正六边形的边心距为,则该正六边形的边长是(
)
A.
B.2
C.3
D.
2.如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列说法错误的是(
)
A.四边形EDCN是菱形
B.四边形MNCD是梯形
C.△AEM与△CBN均为等腰三角形
D.△EAN≌△EDM
3.有一个边长为50cm的正方形洞口,要用一个圆盖去盖住这个洞口,那么圆盖的直径至少应为(
)
A.50cm
B.
C,
D.
4.已知一个圆的半径为5
cm,则它的内接正六边形的边长为(
)
A.4
cm
B.5
cm
C.5.5
cm
D.6
cm
5.半径为a的正六边形的面积等于
A.
B.
C.
D.
6.如图,边长为4的正方形ABCD内接于⊙O,E是弧AB上的一动点(不与A,B重合),F是弧BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①=;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△OGH周长的最小值为4+.其中正确的是( )
A.
①③④
B.
①②③
C.
①②
D.
③④
7.如图,要拧开一个边长为a=6
mm的正六边形螺帽,扳手张开的开口b至少为(
)
A.mm
B.12
mm
C.mm
D.mm
8.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为(
)
A.6,
B.,3
C.6,3
D.,
二、填空题
9.如果一边长为20cm的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过,那么铁圈直径的最小值为
cm(铁丝粗细忽略不计).
10.如图,正方形ABCD的四个顶点分别在⊙O上,P是上不同于点C的任意一点,则∠BPC的度数是
.
11.若一边长为40cm的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过,则铁圈直径的最小值为______
cm.(铁丝粗细忽略不计)
12.如图所示的正六边形
ABCDEF,连结
FD,则∠FDC
的大小为_________.
13.如图是7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是
.
14.已知圆的半径是,则该圆的内接正六边形的面积是
.
15.如果正n边形的中心角为2α,边长为5,那么它的边心距为_____.(用锐角α的三角比表示)
16.如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为__
__.
三、解答题
17.如图①有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心.(下列各题结果精确到0.1m)
(1)求地基的中心到边缘的距离;
(2)己知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?
18.如图,在的内接四边形ABCD中,,点E在上
求的度数;
连接OD、OE,当时,AE恰好为的内接正n边形的一边,求n的值.
19.(1)如图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点,且BM=CN,连接OM,ON,求∠MON的度数。
(2)图②、③、……
④中,M、N分别是⊙O的内接正方形ABCD、正五边ABCDE、……正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON;则图②中∠MON的度数是__________,图③中∠MON的度数是__________;……由此可猜测在n边形图中∠MON的度数是_______
20.如图,已知正六边形ABCDEF,其外接圆的半径是a,求正六边形的周长和面积.
求⊙O的半径.
答案
1.
B
2.
D
3.
C
4.
B
5.
B
6.
C
7.
C
8.
B
9.
10.
45°
11.
12.
90°
13.
14.
15.
(或)
16.
9
17.
(1)作OM⊥AB于点M,连接OA、OB,则OM为边心距,∠AOB是中心角.
由正五边形性质得∠AOB=360°÷5=72°.
又AB=×26=5.2,
∴AM=2.6,∠AOM=36°,
在Rt△AMO中,边心距OM=
(2)3.6-1-1.6=1(m).
答:地基的中心到边缘的距离约为3.6m,塑像底座的半径最大约为1m.
18.
解:连接BD,
四边形ABCD是的内接四边形,
,,
,,
是等边三角形,,
四边形ABDE是的内接四边形,
,;
连接OA,
,
,
,
,
.??
19.
(1)120°
(2)90°、72°、°
20.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
