2020年秋苏科版九年级数学上册随堂练——2.6正多边形与圆学情练习(word 版 含答案)
文档属性
| 名称 | 2020年秋苏科版九年级数学上册随堂练——2.6正多边形与圆学情练习(word 版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 08:26:35 | ||
图片预览

文档简介
2.6正多边形与圆学情练习
一、选择题
1.下列说法中正确的是(
)
A.各边都相等的多边形是正多边形
B.每条边都相等的圆内接多边形是正多边形
C.每个角都相等的圆内接多边形是正多边形
D.每条边都相等的圆外切多边形是正多边形
2.已知⊙O的内接多边形的周长为3,⊙O的外切多边形的周长为3.4,则下列各数中与此圆的周长最接近的是(
)
A.
B.
C.
D.
3.⊙O的半径等于3,则⊙O的内接正方形的边长等于(
)
A.3
B.2
C.3
D.6
4.如果一个圆的内接正六边形的周长为30cm,那么圆的半径为(
).
A.
6
B.
5
C.
4
D.
3
5.已知△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形.若△OAB的一个内角为70°,则该正多边形的边数为(
)
A.7
B.8
C.9
D.10
6.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为(
)
A.6,
B.,3
C.6,3
D.,
7.如图,半径为1的与正六边形ABCDEF相切于点A、D,则的长为
A.
B.
C.
D.
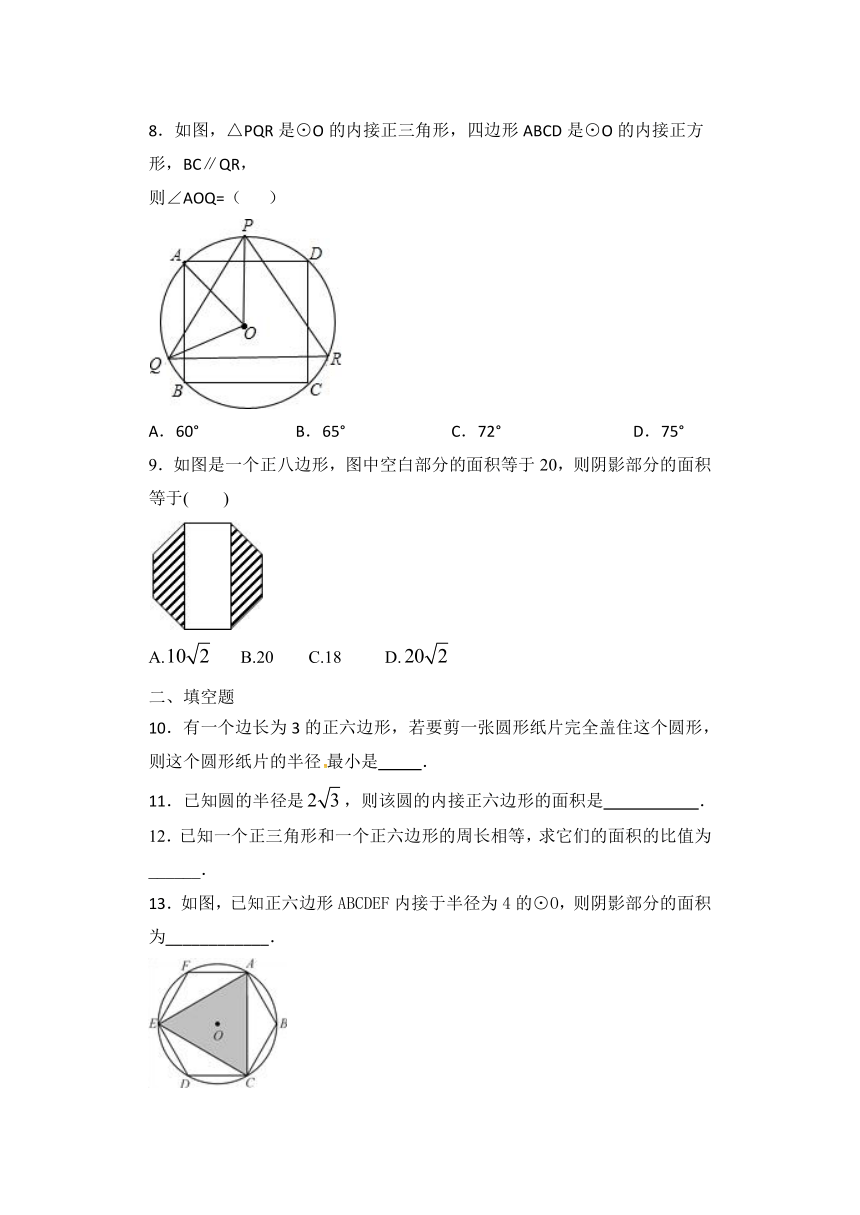
8.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,
则∠AOQ=(
)
A.60°
B.65°
C.72°
D.75°
9.如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于(
)
A.
B.20
C.18
D.
二、填空题
10.有一个边长为3的正六边形,若要剪一张圆形纸片完全盖住这个圆形,则这个圆形纸片的半径最小是
.
11.已知圆的半径是,则该圆的内接正六边形的面积是
.
12.已知一个正三角形和一个正六边形的周长相等,求它们的面积的比值为______.
13.如图,已知正六边形ABCDEF内接于半径为4的⊙O,则阴影部分的面积为____________.
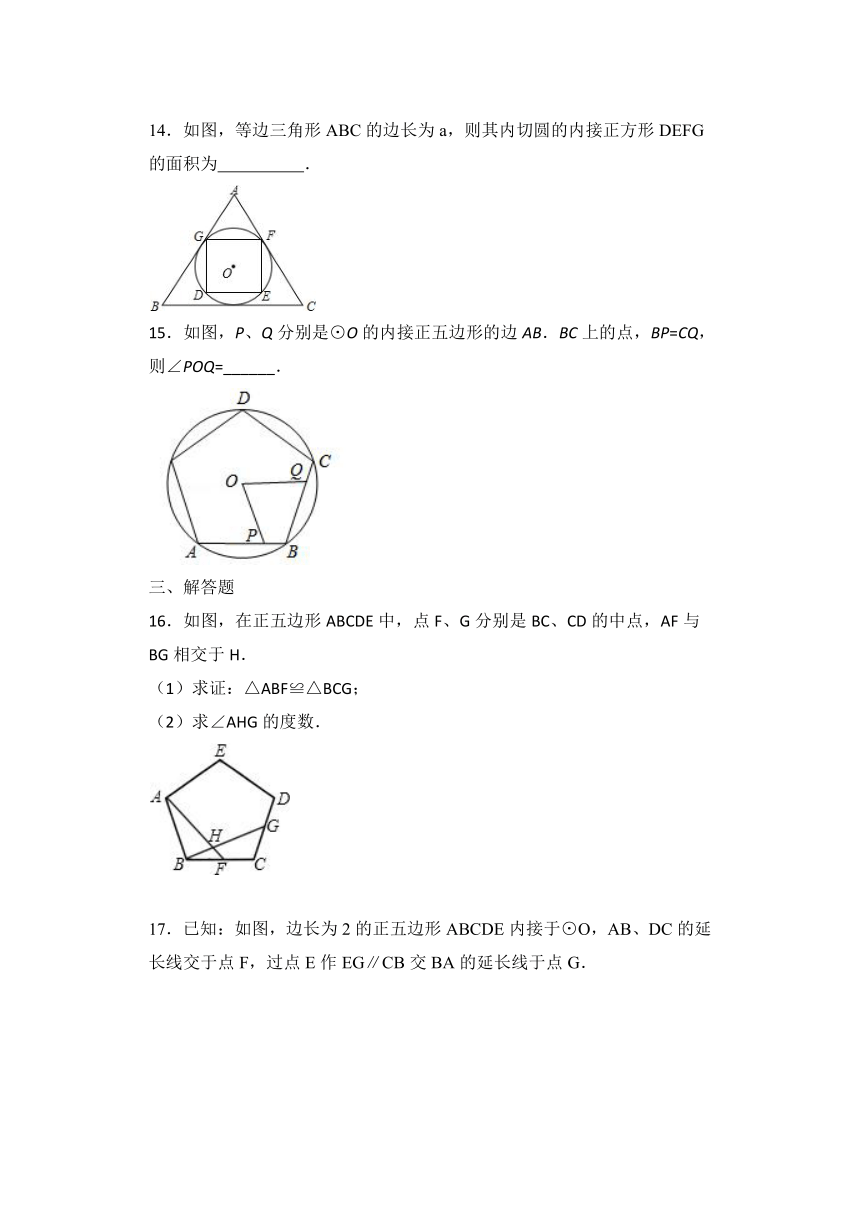
14.如图,等边三角形ABC的边长为a,则其内切圆的内接正方形DEFG的面积为
.
15.如图,P、Q分别是⊙O的内接正五边形的边AB.BC上的点,BP=CQ,则∠POQ=______.
三、解答题
16.如图,在正五边形ABCDE中,点F、G分别是BC、CD的中点,AF与BG相交于H.
(1)求证:△ABF≌△BCG;
(2)求∠AHG的度数.
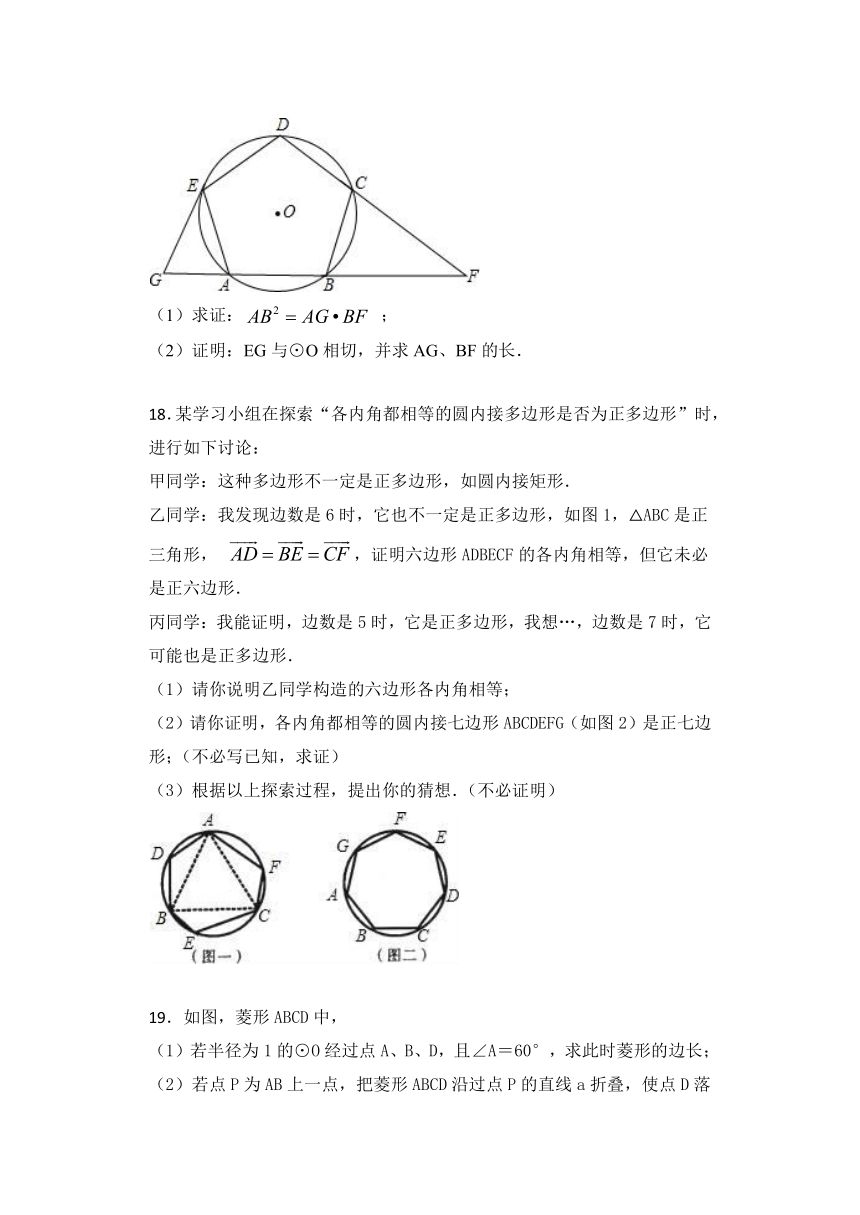
17.已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.
(1)求证:
;
(2)证明:EG与⊙O相切,并求AG、BF的长.
18.某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形,
,证明六边形ADBECF的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求证)
(3)根据以上探索过程,提出你的猜想.(不必证明)
19.如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)
20.如图,在正方形ABCD中,E是边CD的中点.
(1)用直尺和圆规作⊙O,使⊙O经过点A、B、E(保留作图痕迹,不写作法);
(2)若正方形ABCD的边长为2,求(1)中所作⊙O的半径.
答案
1.
B
2.
C
3.
C
4.
B
5.
C
6.
B
7.
C
8.
D
9.
B
10.
3
11.
12.
2:3
13.
12
14.
15.
72°
16.
(1)证明略;(2)108°
17.
证明:(1)易证五边形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,∴∠EAG=∠FBC.∴△EAG∽△FBC.
∴,即BC?AE=AG?BF.
又∵BC=AE=AB,
∴
.①
(2)连接EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,
∴FA=FD,∴EF⊥BC且EF平分BC,∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG,
∴EG与⊙O相切.
∴
.
由(1)可知∠G=∠EAG,∴EG=EA=2,
设AG=x,则
,解得
∴AG=,代入①中可得:BF=
18.
(1)图(1)中六边形各角相等;(2)略(3)猜想:当边数是奇数时(或当边数是3,5,7,9,时),各内角相等的圆内接多边形是正多边形
19.
(1)连接OB、OD和OC,如图所示:
∵半径为1的⊙O经过点A、B、D,且∠A=60°,
∴∠DOB=120°,OD=OB=1,
∵四边形ABCD是菱形,∠A=60°,
∴CD=BC,∠C=60°,
在△COD和△COB中
∴△COD≌△COB(SSS),
∴∠COD=∠COB,∠DCO=∠BCO,
∴∠COD=∠COB=
,
∠DCO=∠BCO=
∴∠ODC=(180-30-60)o=90o,
∴△COD
是Rt△COD,
∵tan∠DCO=
∴CD=tan30o
∴菱形ABCD的边长是
;
(2)如图所示:
作出D在BC上的对应点,再作出直线a即可。
20.
(1)如图1所示:
⊙O即为所求.
(2)如图2,在(1)中设AB的垂直平分线交AB于点F,交CD于点E′.
则AF=AB=1,∠AFE′=90°,
∵四边形ABCD是正方形,
∴∠FAD=∠D=90°,
∴四边形AFE′D是矩形,
∴E′F=AD=2,DE′=AF=1,
∴点E′与点E重合,
连接OA,设⊙O的半径为r,
可得OA=OE=r,
∴OF=EF﹣OE=2﹣r,
∴在Rt△AOF中,AO2=AF2+OF2,
∴r2=12+(2﹣r)2,
∴解得:r=,
∴⊙O的半径为.
一、选择题
1.下列说法中正确的是(
)
A.各边都相等的多边形是正多边形
B.每条边都相等的圆内接多边形是正多边形
C.每个角都相等的圆内接多边形是正多边形
D.每条边都相等的圆外切多边形是正多边形
2.已知⊙O的内接多边形的周长为3,⊙O的外切多边形的周长为3.4,则下列各数中与此圆的周长最接近的是(
)
A.
B.
C.
D.
3.⊙O的半径等于3,则⊙O的内接正方形的边长等于(
)
A.3
B.2
C.3
D.6
4.如果一个圆的内接正六边形的周长为30cm,那么圆的半径为(
).
A.
6
B.
5
C.
4
D.
3
5.已知△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形.若△OAB的一个内角为70°,则该正多边形的边数为(
)
A.7
B.8
C.9
D.10
6.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为(
)
A.6,
B.,3
C.6,3
D.,
7.如图,半径为1的与正六边形ABCDEF相切于点A、D,则的长为
A.
B.
C.
D.
8.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,
则∠AOQ=(
)
A.60°
B.65°
C.72°
D.75°
9.如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于(
)
A.
B.20
C.18
D.
二、填空题
10.有一个边长为3的正六边形,若要剪一张圆形纸片完全盖住这个圆形,则这个圆形纸片的半径最小是
.
11.已知圆的半径是,则该圆的内接正六边形的面积是
.
12.已知一个正三角形和一个正六边形的周长相等,求它们的面积的比值为______.
13.如图,已知正六边形ABCDEF内接于半径为4的⊙O,则阴影部分的面积为____________.
14.如图,等边三角形ABC的边长为a,则其内切圆的内接正方形DEFG的面积为
.
15.如图,P、Q分别是⊙O的内接正五边形的边AB.BC上的点,BP=CQ,则∠POQ=______.
三、解答题
16.如图,在正五边形ABCDE中,点F、G分别是BC、CD的中点,AF与BG相交于H.
(1)求证:△ABF≌△BCG;
(2)求∠AHG的度数.
17.已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.
(1)求证:
;
(2)证明:EG与⊙O相切,并求AG、BF的长.
18.某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形,
,证明六边形ADBECF的各内角相等,但它未必是正六边形.
丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求证)
(3)根据以上探索过程,提出你的猜想.(不必证明)
19.如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)
20.如图,在正方形ABCD中,E是边CD的中点.
(1)用直尺和圆规作⊙O,使⊙O经过点A、B、E(保留作图痕迹,不写作法);
(2)若正方形ABCD的边长为2,求(1)中所作⊙O的半径.
答案
1.
B
2.
C
3.
C
4.
B
5.
C
6.
B
7.
C
8.
D
9.
B
10.
3
11.
12.
2:3
13.
12
14.
15.
72°
16.
(1)证明略;(2)108°
17.
证明:(1)易证五边形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,∴∠EAG=∠FBC.∴△EAG∽△FBC.
∴,即BC?AE=AG?BF.
又∵BC=AE=AB,
∴
.①
(2)连接EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,
∴FA=FD,∴EF⊥BC且EF平分BC,∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG,
∴EG与⊙O相切.
∴
.
由(1)可知∠G=∠EAG,∴EG=EA=2,
设AG=x,则
,解得
∴AG=,代入①中可得:BF=
18.
(1)图(1)中六边形各角相等;(2)略(3)猜想:当边数是奇数时(或当边数是3,5,7,9,时),各内角相等的圆内接多边形是正多边形
19.
(1)连接OB、OD和OC,如图所示:
∵半径为1的⊙O经过点A、B、D,且∠A=60°,
∴∠DOB=120°,OD=OB=1,
∵四边形ABCD是菱形,∠A=60°,
∴CD=BC,∠C=60°,
在△COD和△COB中
∴△COD≌△COB(SSS),
∴∠COD=∠COB,∠DCO=∠BCO,
∴∠COD=∠COB=
,
∠DCO=∠BCO=
∴∠ODC=(180-30-60)o=90o,
∴△COD
是Rt△COD,
∵tan∠DCO=
∴CD=tan30o
∴菱形ABCD的边长是
;
(2)如图所示:
作出D在BC上的对应点,再作出直线a即可。
20.
(1)如图1所示:
⊙O即为所求.
(2)如图2,在(1)中设AB的垂直平分线交AB于点F,交CD于点E′.
则AF=AB=1,∠AFE′=90°,
∵四边形ABCD是正方形,
∴∠FAD=∠D=90°,
∴四边形AFE′D是矩形,
∴E′F=AD=2,DE′=AF=1,
∴点E′与点E重合,
连接OA,设⊙O的半径为r,
可得OA=OE=r,
∴OF=EF﹣OE=2﹣r,
∴在Rt△AOF中,AO2=AF2+OF2,
∴r2=12+(2﹣r)2,
∴解得:r=,
∴⊙O的半径为.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
