苏科版九年级上册 数学 课件: 2.8 圆锥的侧面积(共23张PPT)
文档属性
| 名称 | 苏科版九年级上册 数学 课件: 2.8 圆锥的侧面积(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 251.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
2.8 圆锥的侧面积
一、课前准备:
1.圆周长计算公式:
2.弧长计算公式:
3.扇形面积公式:
L=2πr
L=
S= , S= LR
学习目标:
1. 经历探索圆锥侧面积计算公式的过程;
2.知道圆锥的侧面积计算公式,并会应用公式解决问题.
观 察
二、合作探究:
根据你以前的所学,说说你对圆锥的一些认识。
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线
连接顶点S与底面圆的圆心O的线段叫做圆锥的高
思考圆锥的母线和圆锥的高有那些性质?
圆锥的基本概念:
A
B
O
C
R
母线的长=其侧面展开图扇形的半径
观 察
S
A
O
B
r
S
A
O
B
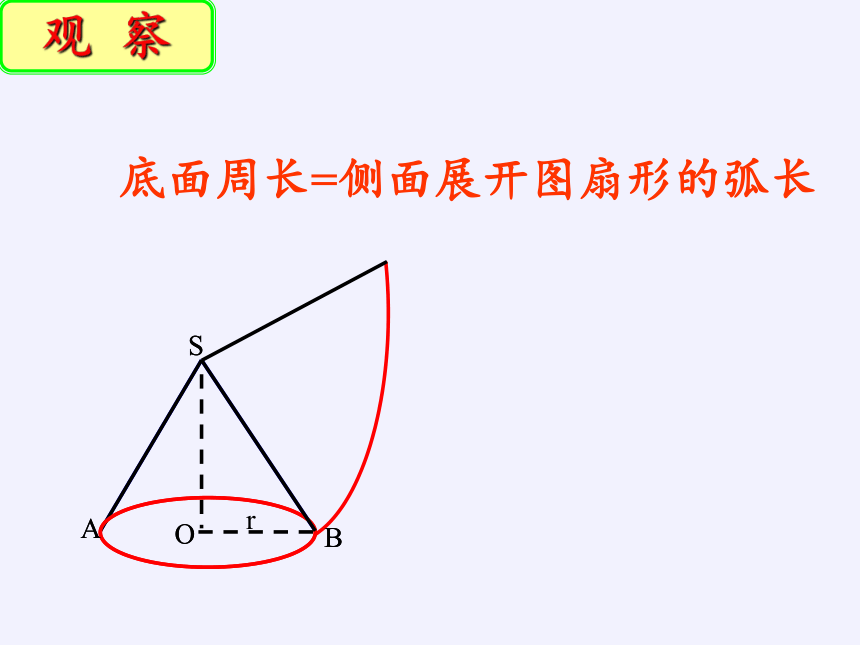
底面周长=侧面展开图扇形的弧长
观 察
A
B
O
C
2.母线的长=其侧面展开图扇形的半径
3.底面周长=侧面展开图扇形的弧长
1.圆锥的侧面展开图是扇形
归纳总结
将圆锥的侧面沿母线
剪开,展开成平面图形,可以得到
一个扇形,设圆锥的底面半径为r,这个扇形的半径等于___________,
扇形的弧长______________.
S圆锥侧=S扇形=_______
= ____ .
S圆锥全=S圆锥侧+S圆锥底面=
_________ +_________
圆锥的母线长
圆锥底面周长
h
r
由勾股定理得:
如果用r表示圆锥底面的半径, h表示圆锥的高线长, 表示圆锥的母线长,那么r,h, 之间有怎样的数量关系呢?
r2+h2= 2
1.已知圆锥的底面半径为80,母线长90,则它的侧面积为______,全面积为_________.
2.一个圆柱形水池的底面半径为5m,池深1.5m,要在池的内壁和底面涂上油漆,总计要涂油漆的面积为________ _.
3.圆锥的侧面展开图的面积为 ,母线长为5,则圆锥的底面半径为_____.
4.一个圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图扇形的圆心角的度数为____度.
5.圆锥侧面展开图是一个半圆,则这个圆锥的母线长与底面半径的比为_______.
三、个性展示:
7200π
7840π
40π
3
180
2:1
6 .制作如图所示的圆锥形铁皮烟囱帽,其尺寸要求为:底面直径80cm,母线长50cm,求烟囱帽铁皮的面积(精确到1cm )
1。如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.
(1)求这个圆锥的底面半径r;
(2)求这个圆锥的高
A
C
O
四、整合提升
2.在半径为的圆形纸片中,剪一个圆心角为90°的扇形
(1)求这个扇形的面积(结果保留);
(2)用所剪的扇形纸片围成一个圆锥的侧面,求这个圆锥的底面圆半径;
(3)在被剪掉的3块余料中,能否从中选取一块剪出一个圆作为“(2)”中所围成的圆锥的底面?
2.如图,用正方形铁皮剪一个圆形和扇形,使之恰好围成一个圆锥,设圆的半径为r,扇形半径为R,试探究圆的半径与扇形半径之间的关系.
S 侧 =πrl
(r表示圆锥底面的半径, l 表示圆锥的母线长 )
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
五、课堂小 结
1.圆锥的母线长为5,高为3,则它的侧面积为_________.
2.圆锥的母线长为13,高为12,它的侧面展开图的弧长为______.
3.用一个半径为6,圆心角为150°的扇形纸片,做成一个圆锥模型的侧面,则这个模型的底面半径为_______.
六、反馈练习:
4.如图,圆锥的母线SA的长为6,SO为圆锥的高,∠ASO=30°.
求这个圆锥的全面积.
20π
10π
2.5
5.如图,扇形的半径为6,圆心角120°,用它做成一个圆锥模型的侧面.求这个圆锥的底面半径和高.
6 .如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)分别以直线AC、BC为轴,把△ABC旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.
如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
A
B
C
思考题
已知如图(1),圆锥的母线长为4,底面圆半径为1,若一小虫P从点A开始绕着圆锥表面爬行一圈到SA的中点C,求小虫爬行的最短距离.
(1)
(2)
本题是将圆锥侧面展开,得一扇形,先求一圆心角。得解。
谢 谢
2.8 圆锥的侧面积
一、课前准备:
1.圆周长计算公式:
2.弧长计算公式:
3.扇形面积公式:
L=2πr
L=
S= , S= LR
学习目标:
1. 经历探索圆锥侧面积计算公式的过程;
2.知道圆锥的侧面积计算公式,并会应用公式解决问题.
观 察
二、合作探究:
根据你以前的所学,说说你对圆锥的一些认识。
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线
连接顶点S与底面圆的圆心O的线段叫做圆锥的高
思考圆锥的母线和圆锥的高有那些性质?
圆锥的基本概念:
A
B
O
C
R
母线的长=其侧面展开图扇形的半径
观 察
S
A
O
B
r
S
A
O
B
底面周长=侧面展开图扇形的弧长
观 察
A
B
O
C
2.母线的长=其侧面展开图扇形的半径
3.底面周长=侧面展开图扇形的弧长
1.圆锥的侧面展开图是扇形
归纳总结
将圆锥的侧面沿母线
剪开,展开成平面图形,可以得到
一个扇形,设圆锥的底面半径为r,这个扇形的半径等于___________,
扇形的弧长______________.
S圆锥侧=S扇形=_______
= ____ .
S圆锥全=S圆锥侧+S圆锥底面=
_________ +_________
圆锥的母线长
圆锥底面周长
h
r
由勾股定理得:
如果用r表示圆锥底面的半径, h表示圆锥的高线长, 表示圆锥的母线长,那么r,h, 之间有怎样的数量关系呢?
r2+h2= 2
1.已知圆锥的底面半径为80,母线长90,则它的侧面积为______,全面积为_________.
2.一个圆柱形水池的底面半径为5m,池深1.5m,要在池的内壁和底面涂上油漆,总计要涂油漆的面积为________ _.
3.圆锥的侧面展开图的面积为 ,母线长为5,则圆锥的底面半径为_____.
4.一个圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图扇形的圆心角的度数为____度.
5.圆锥侧面展开图是一个半圆,则这个圆锥的母线长与底面半径的比为_______.
三、个性展示:
7200π
7840π
40π
3
180
2:1
6 .制作如图所示的圆锥形铁皮烟囱帽,其尺寸要求为:底面直径80cm,母线长50cm,求烟囱帽铁皮的面积(精确到1cm )
1。如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.
(1)求这个圆锥的底面半径r;
(2)求这个圆锥的高
A
C
O
四、整合提升
2.在半径为的圆形纸片中,剪一个圆心角为90°的扇形
(1)求这个扇形的面积(结果保留);
(2)用所剪的扇形纸片围成一个圆锥的侧面,求这个圆锥的底面圆半径;
(3)在被剪掉的3块余料中,能否从中选取一块剪出一个圆作为“(2)”中所围成的圆锥的底面?
2.如图,用正方形铁皮剪一个圆形和扇形,使之恰好围成一个圆锥,设圆的半径为r,扇形半径为R,试探究圆的半径与扇形半径之间的关系.
S 侧 =πrl
(r表示圆锥底面的半径, l 表示圆锥的母线长 )
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
五、课堂小 结
1.圆锥的母线长为5,高为3,则它的侧面积为_________.
2.圆锥的母线长为13,高为12,它的侧面展开图的弧长为______.
3.用一个半径为6,圆心角为150°的扇形纸片,做成一个圆锥模型的侧面,则这个模型的底面半径为_______.
六、反馈练习:
4.如图,圆锥的母线SA的长为6,SO为圆锥的高,∠ASO=30°.
求这个圆锥的全面积.
20π
10π
2.5
5.如图,扇形的半径为6,圆心角120°,用它做成一个圆锥模型的侧面.求这个圆锥的底面半径和高.
6 .如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)分别以直线AC、BC为轴,把△ABC旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.
如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
A
B
C
思考题
已知如图(1),圆锥的母线长为4,底面圆半径为1,若一小虫P从点A开始绕着圆锥表面爬行一圈到SA的中点C,求小虫爬行的最短距离.
(1)
(2)
本题是将圆锥侧面展开,得一扇形,先求一圆心角。得解。
谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
