折叠问题

(共9张PPT)
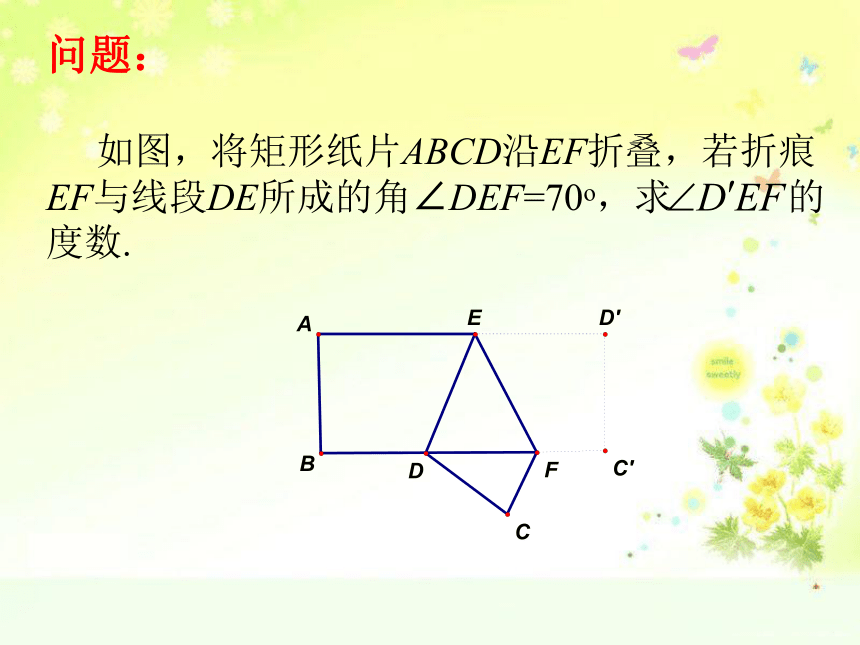
如图，将矩形纸片ABCD沿EF折叠，若折痕EF与线段DE所成的角∠DEF=70o，求 的度数.
问题：
一、概念：
轴对称：
对于两个图形，如果沿一条直线对折后，它们能完全重合，那么称这两个图形成轴对称，这条直线就是对称轴。
二、 轴对称的性质：
2.对应点的连线被对称轴垂直平分；
1.关于某条直线对称的两个图形是全等的.
3.两个图形关于某条直线对称，如果它们的对应线段或其延长线相交，那么交点在对称轴上.
如图，已知矩形ABCD中，BC=10，AB=8，把矩形ABCD沿BD对折，使C点落在E处，BE与AD交于M点．
（1）判断折叠后重叠部分的图形形状，
说明理由.
（2）求AM的长.
例题：
如图，折叠矩形的一边AD，点D落在BC边的点F处，已知AB=8, BC=10 .
求DE的长.
思考：
你还有其他方法求DE的长吗？
练习：
D
C
F
A
B
E
如图，已知矩形ABCD中，BC=8，AB=6，将矩形ABCD折叠，使AB落在对角线AC上，点B落在点F处，折痕AE交BC于点E，求线段EF长.
自我提升：
D
A
B
F
E
C
总结：
1.本质：轴对称（全等性）
2.关键：根据折叠实现等量的转化
3.解题基本方法：构造方程
（1）根据勾股定理得方程。
（2）根据相似比得方程。
折叠问题莫心急
全等性质应找齐
结合已知挖关系
方程思想要记清
感谢各位老师莅临指导！