沪教版上海九年级数学上册 第24章相似三角形单元测试卷(word 版 含解析)
文档属性
| 名称 | 沪教版上海九年级数学上册 第24章相似三角形单元测试卷(word 版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 306.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 08:39:25 | ||
图片预览




文档简介
第二十四章
相似三角形
单元测试卷
一、选择题
1.△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A.27
B.
12
C.
18
D.
20
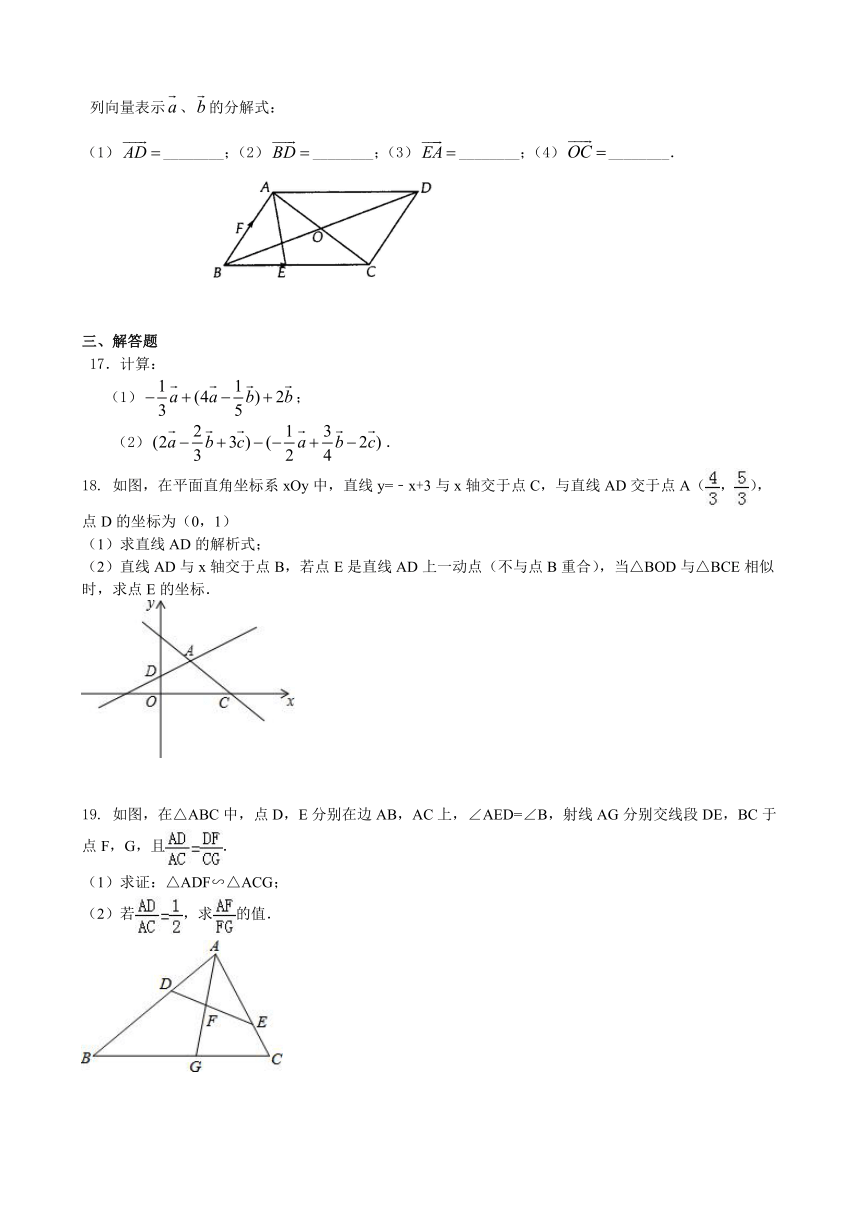
2.如图,小明设计两个直角,来测量河宽BC,他量得AB=20米,BD=30米,CE=90米,则河宽BC为(
)
A.50米
B.40米
C.60米
D.80米
3.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是(
)
A.19
B.17
C.24
D.21
4.如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2,CD=,点P在四边形ABCD的边上.若P到BD的距离为,则点P的个数为(
)
A.1
B.2
C.3
D.4
第2题
第4题
第5题
5.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度(
)
A.增大1.5米
B.减小1.5米
C.增大3.5米
D.减小3.5米
6.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=6,在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为(
)
A.8 B.
C.8或
D.8或9
7.如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有(
)
①
;
②
;
③
;④CE2=CD×BC;
⑤BE2=AE×BC
A.2个
B.3个
C.4个
D.5个
第6题
第7题
第8题
8.如图,已知△ABC中,两条中线AE、CF交于点G,设,,则向量关于、的分解式表示正确的为(
)
A.
B.
C.
D.
二、填空题
9.如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是
.
10.如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC= .
11.如图,在△ABC中,D、E分别是AB和AC中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC=_______,△ADE与△ABC的面积之比为_______,△CFG与△BFD的面积之比为________.
12.如图,在口ABCD中,AD=10厘米,CD=6厘米,E为AD上一点,且BE=BC,CE=CD,则DE=
厘米.
13.
如图,口ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为a,则口ABCD的面积为
.(用a的代数式表示)
第12题
第13题
第14题
14.如图,M是ABCD的边AB的中点,CM交BD于E,则图中阴影部分的面积与ABCD的面积之比为_____.
15.若,,,则用向量、表示________.
16.如图,在口ABCD中,点F是AB的中点,点E在BC上,且BC=3BE,设,,那么将下列向量表示、的分解式:
(1)________;(2)________;(3)________;(4)________.
解答题
17.计算:
(1);
(2).
18.
如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A(,),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
19.
如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.
(1)求证:△ADF∽△ACG;
(2)若,求的值.
20.类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在□ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若,求的值.
(1)尝试探究
在图1中,过点E作交BG于点H,则AB和EH的数量关系是
,CG和EH的数量关系是
,的值是
(2)类比延伸
如图2,在原题的条件下,若则的值是
(用含的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若,则的值是
(用含的代数式表示).
21.如图,在Rt△ABC中,∠ACB=90?,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设,,
求关于的函数解析式,并写出函数的定义域;
(3)在点E、F移动过程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.
22.
如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm,动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,
Q两点同时停止运动.以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形APDE和梯形BCFQ重合部分的面积为Scm?.
(1)当t=_____s时,点P与点Q重合;
(2)当t=_____s时,点D在QF上;
(3)当点P在Q,
B两点之间(不包括
Q,
B两点)时,求S与t之间的函数关系式.
答案与解析
一、选择题
1.【答案】C;
【解析】设另一个三角形最短的一边是x,
∵△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,
∴=,
解得x=18.故选C.
2.【答案】B;
【解析】.
3.【答案】C;
【解析】用相似三角形的对应边的比相等求出其他两边,再求和.
4.【答案】B;
【解析】A到BD的距离为2,故在AB、AD存在P.
5.【答案】D;
【解析】由题意,,
由相似,,
同理,.
6.【答案】C;
【解析】如图,情况分两种:
7.【答案】B;
【解析】②③④成立.
8.【答案】B.
二、填空题
9.【答案】7.
【解析】∵△ABC与△DEC的面积相等,
∴△CDF与四边形AFEB的面积相等,
∵AB∥DE,
∴△CEF∽△CBA,
∵EF=9,AB=12,
∴EF:AB=9:12=3:4,
∴△CEF和△CBA的面积比=9:16,
设△CEF的面积为9k,则四边形AFEB的面积=7k,
∵△CDF与四边形AFEB的面积相等,
∴S△CDF=7k,
∵△CDF与△CEF是同高不同底的三角形,
∴面积比等于底之比,
∴DF:EF=7k:9k,
∴DF=7.
故答案为:7.
10.【答案】4.8或;
【解析】∵在Rt△ABC中,AC=8,BC=6,
∴AB==10,
当△ABC∽△PCA时,则
AB:PC=BC:AC,
即10:PC=6:8,
解得:PC=,
当△ABC∽ACP△时,则
AB:AC=BC:PC,
即10:8=6:PC,
解得:PC=4.8.
综上可知若△ABC与△PAC相似,则PC=4.8或.
11.【答案】2;1:4;1:6;
【解析】由题意,,且,
,又,
.
12.【答案】3.6;
【解析】△BCE与△CDE均为等腰三角形,且两个底角∠DEC=∠BCE,∴△BCE∽△CDE,
∴=,∴
=,∴DE=3.6厘米.
13.【答案】12a;
【解析】根据四边形ABCD是平行四边形,利用已知得出△DEF∽△CEB,△DEF∽△ABF,进而利用相似三角形的性质分别得出△CEB、△ABF的面积为4a、9a,然后推出四边形BCDF的面积为8a即可.
14.【答案】;
【解析】,,
(三角形等高,面积比等于底边比)
,
阴影部分的面积与ABCD的面积之比为1:3.
15.【答案】;
16.【答案】(1);
(2);
(3);
(4).
解答题
17.【答案与解析】
(1);
(2).
18.【答案与解析】
解:(1)设直线AD的解析式为y=kx+b,
将A(,),D(0,1)代入得:,
解得:.
故直线AD的解析式为:y=x+1;
(2)∵直线AD与x轴的交点为(﹣2,0),
∴OB=2,
∵点D的坐标为(0,1),
∴OD=1,
∵y=﹣x+3与x轴交于点C(3,0),
∴OC=3,
∴BC=5
∵△BOD与△BEC相似,
∴或,
∴==或,
∴BE=2,CE=,或CE=,
∴E(2,2),或(3,).
19.【答案与解析】
(1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C,
∵=,
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,
∴=,
又∵=,
∴=,
∴=1.
20.【答案与解析】
(1)
(2)
作EH∥AB交BG于点H,则△EHF∽△ABF,
∴
∵AB=CD,∴
∵EH∥AB∥CD,∴△BEH∽△BCG,
∴,∴CG=2EH,
∴
(3).
提示:此问是(1)、(2)类比、拓展延伸,根据前面问题研究方法,要利用所给条件,所以添加如图3,过点E作EH∥AB交BD的延长线于点H,则有,,两式相比就可得出
21.【答案与解析】
(1)∵∠ACB=900,AB=10,AC=6
∴BC=8
∵ED⊥AB
∴∠ADE=∠ACB=90°
又∵∠A=∠A
∴△ADE∽△ACB
∴
∴
∴DE=4
(2)∵FG⊥AB
∴∠BGF=∠BCA=90°
又∵∠B=∠B
∴△BGF∽△BCA
∴
∴)
∴()
(3)由(1)(2)可得:,
∴,
当∠A=∠CEF时,,解得:;
当∠A=∠CFE时,,解得:
∴当AD的长为或,△AED与△CEF相似.
22.【答案与解析】
(1)∵P,
Q的运动速度都是1cm/s,
∴P,
Q在AB的中点重合.
∴当t=1s时,P,
Q重合.
(2)∵QF‖AC
∴,即,
∴AF=4-2t,
又∵DP‖AF,
∴,即,
.
(3)①当1<t≤时,如图1、图2.
∵FQ‖BC,
∴,即AF=4-2t,EF=4-3t,
又∵DE‖AB,
∴△FEG∽△FAQ得,,,
EG=,
∴GD=t-()=,
QP=AP-AQ=t-(2-t)=2t-2,
S=
②当时,由△AFQ∽△ABC得,,AF=4-2x.
∴
同理由△CEH∽△CBA可得EH=,HD=;△BPG∽△BAC,得PG=4-2t,DG=t-(4-2t)=3t-4
∴S=
=
=.
相似三角形
单元测试卷
一、选择题
1.△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A.27
B.
12
C.
18
D.
20
2.如图,小明设计两个直角,来测量河宽BC,他量得AB=20米,BD=30米,CE=90米,则河宽BC为(
)
A.50米
B.40米
C.60米
D.80米
3.一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是(
)
A.19
B.17
C.24
D.21
4.如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=2,CD=,点P在四边形ABCD的边上.若P到BD的距离为,则点P的个数为(
)
A.1
B.2
C.3
D.4
第2题
第4题
第5题
5.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度(
)
A.增大1.5米
B.减小1.5米
C.增大3.5米
D.减小3.5米
6.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=6,在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为(
)
A.8 B.
C.8或
D.8或9
7.如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有(
)
①
;
②
;
③
;④CE2=CD×BC;
⑤BE2=AE×BC
A.2个
B.3个
C.4个
D.5个
第6题
第7题
第8题
8.如图,已知△ABC中,两条中线AE、CF交于点G,设,,则向量关于、的分解式表示正确的为(
)
A.
B.
C.
D.
二、填空题
9.如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是
.
10.如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC= .
11.如图,在△ABC中,D、E分别是AB和AC中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC=_______,△ADE与△ABC的面积之比为_______,△CFG与△BFD的面积之比为________.
12.如图,在口ABCD中,AD=10厘米,CD=6厘米,E为AD上一点,且BE=BC,CE=CD,则DE=
厘米.
13.
如图,口ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为a,则口ABCD的面积为
.(用a的代数式表示)
第12题
第13题
第14题
14.如图,M是ABCD的边AB的中点,CM交BD于E,则图中阴影部分的面积与ABCD的面积之比为_____.
15.若,,,则用向量、表示________.
16.如图,在口ABCD中,点F是AB的中点,点E在BC上,且BC=3BE,设,,那么将下列向量表示、的分解式:
(1)________;(2)________;(3)________;(4)________.
解答题
17.计算:
(1);
(2).
18.
如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A(,),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
19.
如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.
(1)求证:△ADF∽△ACG;
(2)若,求的值.
20.类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在□ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若,求的值.
(1)尝试探究
在图1中,过点E作交BG于点H,则AB和EH的数量关系是
,CG和EH的数量关系是
,的值是
(2)类比延伸
如图2,在原题的条件下,若则的值是
(用含的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若,则的值是
(用含的代数式表示).
21.如图,在Rt△ABC中,∠ACB=90?,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设,,
求关于的函数解析式,并写出函数的定义域;
(3)在点E、F移动过程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.
22.
如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm,动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,
Q两点同时停止运动.以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形APDE和梯形BCFQ重合部分的面积为Scm?.
(1)当t=_____s时,点P与点Q重合;
(2)当t=_____s时,点D在QF上;
(3)当点P在Q,
B两点之间(不包括
Q,
B两点)时,求S与t之间的函数关系式.
答案与解析
一、选择题
1.【答案】C;
【解析】设另一个三角形最短的一边是x,
∵△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,
∴=,
解得x=18.故选C.
2.【答案】B;
【解析】.
3.【答案】C;
【解析】用相似三角形的对应边的比相等求出其他两边,再求和.
4.【答案】B;
【解析】A到BD的距离为2,故在AB、AD存在P.
5.【答案】D;
【解析】由题意,,
由相似,,
同理,.
6.【答案】C;
【解析】如图,情况分两种:
7.【答案】B;
【解析】②③④成立.
8.【答案】B.
二、填空题
9.【答案】7.
【解析】∵△ABC与△DEC的面积相等,
∴△CDF与四边形AFEB的面积相等,
∵AB∥DE,
∴△CEF∽△CBA,
∵EF=9,AB=12,
∴EF:AB=9:12=3:4,
∴△CEF和△CBA的面积比=9:16,
设△CEF的面积为9k,则四边形AFEB的面积=7k,
∵△CDF与四边形AFEB的面积相等,
∴S△CDF=7k,
∵△CDF与△CEF是同高不同底的三角形,
∴面积比等于底之比,
∴DF:EF=7k:9k,
∴DF=7.
故答案为:7.
10.【答案】4.8或;
【解析】∵在Rt△ABC中,AC=8,BC=6,
∴AB==10,
当△ABC∽△PCA时,则
AB:PC=BC:AC,
即10:PC=6:8,
解得:PC=,
当△ABC∽ACP△时,则
AB:AC=BC:PC,
即10:8=6:PC,
解得:PC=4.8.
综上可知若△ABC与△PAC相似,则PC=4.8或.
11.【答案】2;1:4;1:6;
【解析】由题意,,且,
,又,
.
12.【答案】3.6;
【解析】△BCE与△CDE均为等腰三角形,且两个底角∠DEC=∠BCE,∴△BCE∽△CDE,
∴=,∴
=,∴DE=3.6厘米.
13.【答案】12a;
【解析】根据四边形ABCD是平行四边形,利用已知得出△DEF∽△CEB,△DEF∽△ABF,进而利用相似三角形的性质分别得出△CEB、△ABF的面积为4a、9a,然后推出四边形BCDF的面积为8a即可.
14.【答案】;
【解析】,,
(三角形等高,面积比等于底边比)
,
阴影部分的面积与ABCD的面积之比为1:3.
15.【答案】;
16.【答案】(1);
(2);
(3);
(4).
解答题
17.【答案与解析】
(1);
(2).
18.【答案与解析】
解:(1)设直线AD的解析式为y=kx+b,
将A(,),D(0,1)代入得:,
解得:.
故直线AD的解析式为:y=x+1;
(2)∵直线AD与x轴的交点为(﹣2,0),
∴OB=2,
∵点D的坐标为(0,1),
∴OD=1,
∵y=﹣x+3与x轴交于点C(3,0),
∴OC=3,
∴BC=5
∵△BOD与△BEC相似,
∴或,
∴==或,
∴BE=2,CE=,或CE=,
∴E(2,2),或(3,).
19.【答案与解析】
(1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C,
∵=,
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,
∴=,
又∵=,
∴=,
∴=1.
20.【答案与解析】
(1)
(2)
作EH∥AB交BG于点H,则△EHF∽△ABF,
∴
∵AB=CD,∴
∵EH∥AB∥CD,∴△BEH∽△BCG,
∴,∴CG=2EH,
∴
(3).
提示:此问是(1)、(2)类比、拓展延伸,根据前面问题研究方法,要利用所给条件,所以添加如图3,过点E作EH∥AB交BD的延长线于点H,则有,,两式相比就可得出
21.【答案与解析】
(1)∵∠ACB=900,AB=10,AC=6
∴BC=8
∵ED⊥AB
∴∠ADE=∠ACB=90°
又∵∠A=∠A
∴△ADE∽△ACB
∴
∴
∴DE=4
(2)∵FG⊥AB
∴∠BGF=∠BCA=90°
又∵∠B=∠B
∴△BGF∽△BCA
∴
∴)
∴()
(3)由(1)(2)可得:,
∴,
当∠A=∠CEF时,,解得:;
当∠A=∠CFE时,,解得:
∴当AD的长为或,△AED与△CEF相似.
22.【答案与解析】
(1)∵P,
Q的运动速度都是1cm/s,
∴P,
Q在AB的中点重合.
∴当t=1s时,P,
Q重合.
(2)∵QF‖AC
∴,即,
∴AF=4-2t,
又∵DP‖AF,
∴,即,
.
(3)①当1<t≤时,如图1、图2.
∵FQ‖BC,
∴,即AF=4-2t,EF=4-3t,
又∵DE‖AB,
∴△FEG∽△FAQ得,,,
EG=,
∴GD=t-()=,
QP=AP-AQ=t-(2-t)=2t-2,
S=
②当时,由△AFQ∽△ABC得,,AF=4-2x.
∴
同理由△CEH∽△CBA可得EH=,HD=;△BPG∽△BAC,得PG=4-2t,DG=t-(4-2t)=3t-4
∴S=
=
=.
