沪教版上海九年级上册数学第二十四章相似三角形本章测试卷(word 版 含答案)
文档属性
| 名称 | 沪教版上海九年级上册数学第二十四章相似三角形本章测试卷(word 版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-25 00:00:00 | ||
图片预览


文档简介
第二十四章
相似三角形
本章测试卷
一、选择题
1.如果=,那么的值是( )
A.
B.
C.
D.
2.下列各线段中能成比例的是(
)
A.cm、3cm、2cm、cm
B.4cm、6cm、5cm、10cm
C.2cm、cm、cm、cm
D.2cm、3cm、4cm、1cm
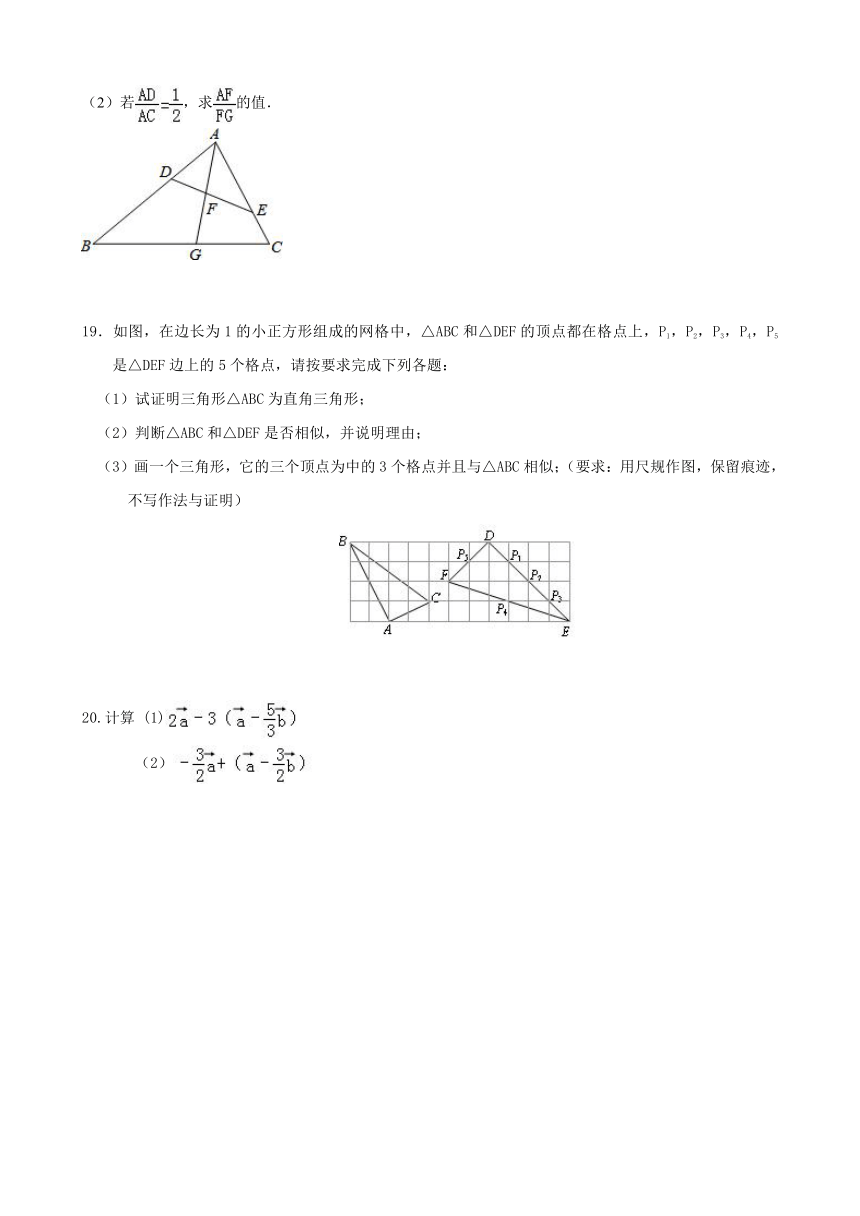
3.如图,△ABC中,点D、E分别是AB、AC的中点,下列结论不正确的是(
)
A.BC=2DE
B.
△ADE∽△ABC
C.
D.
4.如图,在菱形ABCD中,E是BC边上的点,连接AE交BD于点F,
若EC=2BE,则的值是(
)
A.
B.
C.
D.
第3题
第4题
第5题
5.如图,已知直线a∥b∥c,直线m、n
与a、b、c分别交于点A、C、E、B、D、F,AC
=
4,
CE
=
6,BD
=
3,则BF
=(
)
A.
7
B.
7.5
C.
8
D.
8.5
6.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是(
)
7.若O为平行四边形ABCD的中心,,,则(
)
A.
B.
C.
D.
8.已知向量,,若,不平行,则向量与的关系是(
)
A.不平行
B.平行
C.相等
D.无法确定
二、填空题
9.若,
则的值为
.
10.已知数3,6,请再写出一个数,使这三个数中的一个数是另外两个数的比例中项,这个数是___________(只需填写一个数)。
11.如图,在△ABC中,MN∥BC,若∠C=68°,AM:MB=1:2,则∠MNA=_______度,AN:NC=_____________.
12.如图,点D,E分别在AB、AC上,且∠ABC=∠AED。若DE=4,AE=5,BC=8,则AB的长为_________.
第11题
第12题
13.
若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为
.
14.
在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在地面上的影长为40米,则古塔高为________.
15.如图,已知在△ABC中,D、E分别是边AB、边AC的中点,=,=,那么向量用向量,表示为 .
16.若,.其中、是已知向量,则________,________.
三、解答题
17.
已知:a,b,c为三角形三边长,(a-c):(c+b):(c-b)=2:7:(-1),周长为24.求三边长.
18.
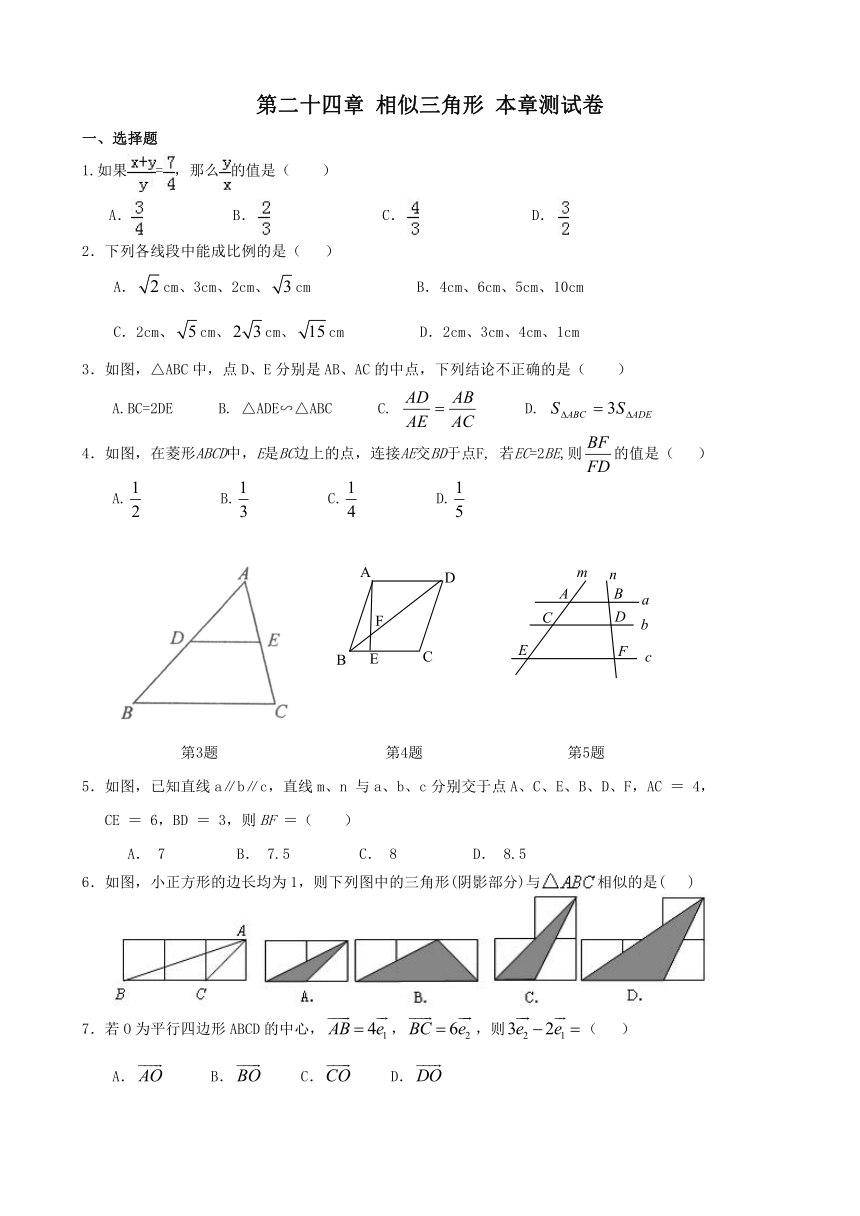
如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.
(1)求证:△ADF∽△ACG;
(2)若,求的值.
19.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明三角形△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,它的三个顶点为中的3个格点并且与△ABC相似;(要求:用尺规作图,保留痕迹,不写作法与证明)
20.计算
(1)
(2)
【答案与解析】
一、选择题
1.【答案】C;
【解析】=,
得=,
所以=,故选:C.
2.【答案】C;
【解析】找两条线段的比等于另两条线段的比即可.
3.【答案】D;
【解析】根据三角形中位线定义与性质可知,BC=2DE;因DE//BC,
所以△ADE∽△ABC,AD:AB=AE:AC,即AD:AE=AB:AC,.
所以选项D错误.
4.【答案】B;
【解析】由菱形ABCD得AD∥BE,,所以△BEF∽△ADF,
又由EC=2BE,得AD=BC=3BE,
故==.故选B.
5.【答案】B;
【解析】由a∥b∥c得BF=7.5,故选B.
6.【答案】A;
【解析】根据相似三角形的判定.
7.【答案】B;
8.【答案】B.
二、填空题
9.【答案】
;
【解析】设,则x=3k,
y=4k,
z=5k
∴.
10.【答案】 3(或-3,或12,或);
【解析】因为此题是一个主观性质的试题,它不是求这两个数的比例中项。而是让自己写出一个数,使三个数中的某个数是另外两个数的比例中项,所以只要明白比例中项的意义,就能写出符合条件的一个数(结论不是唯一的).
11.【答案】68°,1:2;
【解析】首先,想到定理的含义,再结合图形分析(或进行比例变形)就可直接求出结果.
12.【答案】10;
【解析】∵∠ABC=∠AED,∠BAC=∠EAD∴△AED∽△ABC,∴,DE=10.
13.【答案】5:4.
【解析】∵△ABC与△DEF相似且面积之比为25:16,∴△ABC与△DEF的相似比为5:4;∴△ABC与△DEF的周长之比为5:4.
14.【答案】30米;
15.【答案】﹣;
【解析】∵=,=,
∴=﹣=﹣,
∵在△ABC中,D、E分别是边AB、边AC的中点,
∴==(﹣)=﹣.
16.【答案】;
;
三、解答题
17.【答案与解析】
解法1:由题意得:
解法2:由题意设a-c=2k,c+b=7k,c-b=-k则得
把K看成常数,解得a=5k,b=4k,c=3k,因为三角形的周长是24,则有a+b+c=12k=24,
∴k=2, ∴a=5k=10,b=4k=8,c=3k=6
18.【答案与解析】
(1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C,
∵=,
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,
∴=,
又∵=,
∴=,
∴=1.
19.【答案与解析】
(1)根据勾股定理,得,,BC=5
;
显然有,
根据勾股定理的逆定理得△ABC
为直角三角形;
(2)△ABC和△DEF相似.
根据勾股定理,得,,BC=5
,,.
,
∴△ABC∽△DEF.
(3)如图:△P2P4
P5.
20.【答案与解析】
解:(1)原式=2﹣3+5=﹣+5.
(2)原式=﹣+﹣=﹣﹣.
相似三角形
本章测试卷
一、选择题
1.如果=,那么的值是( )
A.
B.
C.
D.
2.下列各线段中能成比例的是(
)
A.cm、3cm、2cm、cm
B.4cm、6cm、5cm、10cm
C.2cm、cm、cm、cm
D.2cm、3cm、4cm、1cm
3.如图,△ABC中,点D、E分别是AB、AC的中点,下列结论不正确的是(
)
A.BC=2DE
B.
△ADE∽△ABC
C.
D.
4.如图,在菱形ABCD中,E是BC边上的点,连接AE交BD于点F,
若EC=2BE,则的值是(
)
A.
B.
C.
D.
第3题
第4题
第5题
5.如图,已知直线a∥b∥c,直线m、n
与a、b、c分别交于点A、C、E、B、D、F,AC
=
4,
CE
=
6,BD
=
3,则BF
=(
)
A.
7
B.
7.5
C.
8
D.
8.5
6.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是(
)
7.若O为平行四边形ABCD的中心,,,则(
)
A.
B.
C.
D.
8.已知向量,,若,不平行,则向量与的关系是(
)
A.不平行
B.平行
C.相等
D.无法确定
二、填空题
9.若,
则的值为
.
10.已知数3,6,请再写出一个数,使这三个数中的一个数是另外两个数的比例中项,这个数是___________(只需填写一个数)。
11.如图,在△ABC中,MN∥BC,若∠C=68°,AM:MB=1:2,则∠MNA=_______度,AN:NC=_____________.
12.如图,点D,E分别在AB、AC上,且∠ABC=∠AED。若DE=4,AE=5,BC=8,则AB的长为_________.
第11题
第12题
13.
若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为
.
14.
在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在地面上的影长为40米,则古塔高为________.
15.如图,已知在△ABC中,D、E分别是边AB、边AC的中点,=,=,那么向量用向量,表示为 .
16.若,.其中、是已知向量,则________,________.
三、解答题
17.
已知:a,b,c为三角形三边长,(a-c):(c+b):(c-b)=2:7:(-1),周长为24.求三边长.
18.
如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.
(1)求证:△ADF∽△ACG;
(2)若,求的值.
19.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明三角形△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,它的三个顶点为中的3个格点并且与△ABC相似;(要求:用尺规作图,保留痕迹,不写作法与证明)
20.计算
(1)
(2)
【答案与解析】
一、选择题
1.【答案】C;
【解析】=,
得=,
所以=,故选:C.
2.【答案】C;
【解析】找两条线段的比等于另两条线段的比即可.
3.【答案】D;
【解析】根据三角形中位线定义与性质可知,BC=2DE;因DE//BC,
所以△ADE∽△ABC,AD:AB=AE:AC,即AD:AE=AB:AC,.
所以选项D错误.
4.【答案】B;
【解析】由菱形ABCD得AD∥BE,,所以△BEF∽△ADF,
又由EC=2BE,得AD=BC=3BE,
故==.故选B.
5.【答案】B;
【解析】由a∥b∥c得BF=7.5,故选B.
6.【答案】A;
【解析】根据相似三角形的判定.
7.【答案】B;
8.【答案】B.
二、填空题
9.【答案】
;
【解析】设,则x=3k,
y=4k,
z=5k
∴.
10.【答案】 3(或-3,或12,或);
【解析】因为此题是一个主观性质的试题,它不是求这两个数的比例中项。而是让自己写出一个数,使三个数中的某个数是另外两个数的比例中项,所以只要明白比例中项的意义,就能写出符合条件的一个数(结论不是唯一的).
11.【答案】68°,1:2;
【解析】首先,想到定理的含义,再结合图形分析(或进行比例变形)就可直接求出结果.
12.【答案】10;
【解析】∵∠ABC=∠AED,∠BAC=∠EAD∴△AED∽△ABC,∴,DE=10.
13.【答案】5:4.
【解析】∵△ABC与△DEF相似且面积之比为25:16,∴△ABC与△DEF的相似比为5:4;∴△ABC与△DEF的周长之比为5:4.
14.【答案】30米;
15.【答案】﹣;
【解析】∵=,=,
∴=﹣=﹣,
∵在△ABC中,D、E分别是边AB、边AC的中点,
∴==(﹣)=﹣.
16.【答案】;
;
三、解答题
17.【答案与解析】
解法1:由题意得:
解法2:由题意设a-c=2k,c+b=7k,c-b=-k则得
把K看成常数,解得a=5k,b=4k,c=3k,因为三角形的周长是24,则有a+b+c=12k=24,
∴k=2, ∴a=5k=10,b=4k=8,c=3k=6
18.【答案与解析】
(1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C,
∵=,
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,
∴=,
又∵=,
∴=,
∴=1.
19.【答案与解析】
(1)根据勾股定理,得,,BC=5
;
显然有,
根据勾股定理的逆定理得△ABC
为直角三角形;
(2)△ABC和△DEF相似.
根据勾股定理,得,,BC=5
,,.
,
∴△ABC∽△DEF.
(3)如图:△P2P4
P5.
20.【答案与解析】
解:(1)原式=2﹣3+5=﹣+5.
(2)原式=﹣+﹣=﹣﹣.
