1.1 探索勾股定理(1)

(共16张PPT)
1.1 (1)探索勾股定理
-毕达哥拉斯定理、商高定理、百牛定理
1
1
毕达哥拉斯（公元前572—前497年），古希腊著名的哲学家、数学家、天文学家.
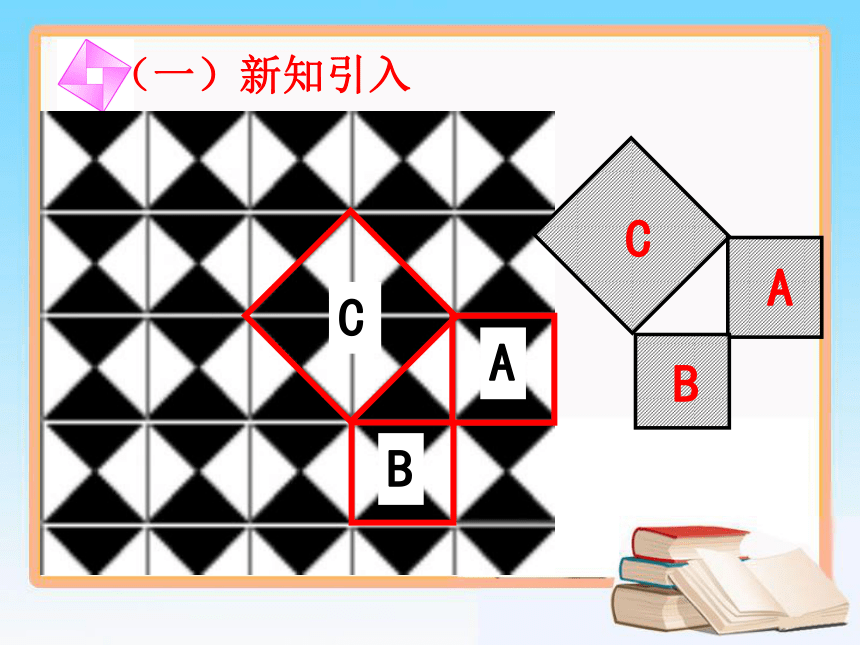
（一）新知引入
黑白相间的地砖
相传两千多年前，古希腊著名的数学家毕达哥拉斯去朋友家做客。在宴席上，其他的宾客都在尽情欢乐，只有毕达哥拉斯却看着朋友家的方砖地发起呆来。原来，朋友家的地是用一块块直角三角形形状的砖铺成的，黑白相间，非常美观大方。主人看到毕达哥拉斯的样子非常奇怪，就想过去问他，谁知，毕达哥拉斯突然恍然大悟的样子，站起来，大笑着跑回家去了。原来，他发现了地砖上的三个正方形存在某种数学关系。
数学小故事
（一）新知引入
A
B
A
B
C
C
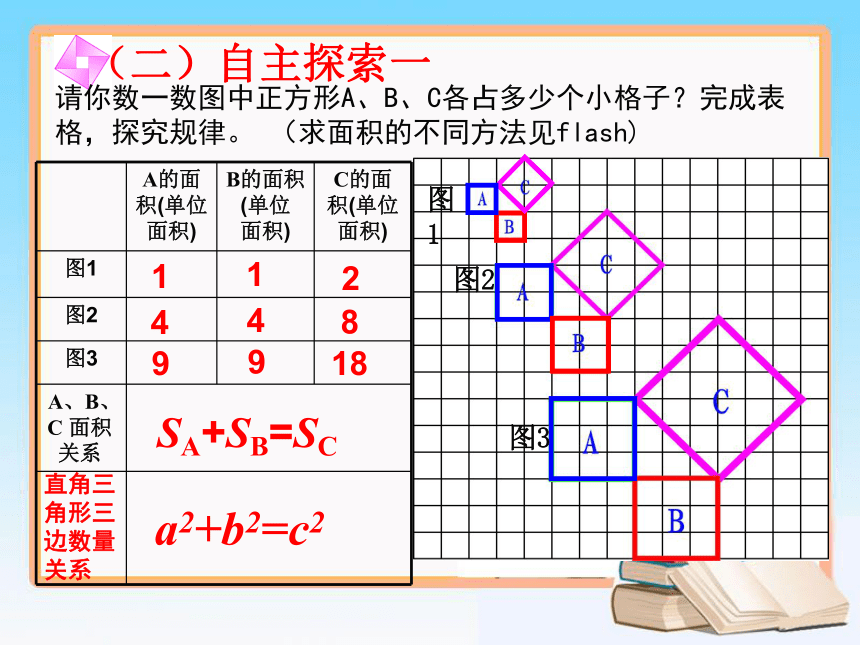
（二）自主探索一
A的面积(单位 面积) B的面积(单位 面积) C的面积(单位 面积)
图1
图2
图3
A、B、C 面积 关系
1
1
2
4
4
8
9
9
18
SA+SB=SC
a2+b2=c2
请你数一数图中正方形A、B、C各占多少个小格子？完成表格，探究规律。 （求面积的不同方法见flash)
图1
图2
图3
直角三角形三边数量关系
图2
图1
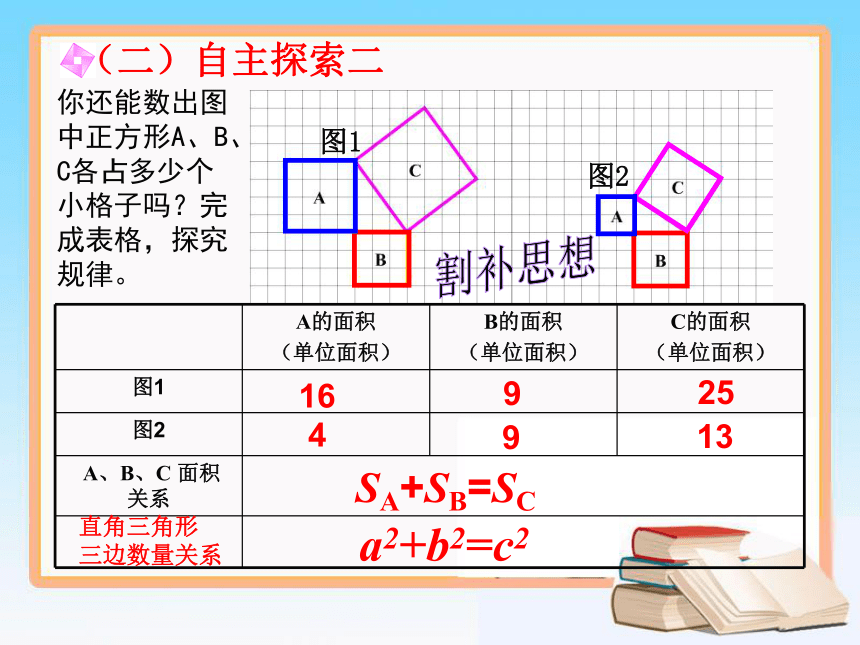
A的面积
（单位面积） B的面积
（单位面积） C的面积
（单位面积）
图1
图2
A、B、C 面积 关系
16
9
25
4
9
13
SA+SB=SC
a2+b2=c2
（二）自主探索二
你还能数出图中正方形A、B、C各占多少个小格子吗？完成表格，探究规律。
直角三角形
三边数量关系
（二）自主探索三
a2+b2=c2
勾
股
弦
《周髀算经》
勾 广 三
股 修 四
径 隅 五
（三）归纳结论
直角三角形两直角边的平方和等于斜边的平方。
如果用a、b、c分别表示直角三角形的两直角边和斜边，那么a2+b2=c2。
勾股定理：
（四）实践应用一，定理应用
1、在△ABC中，∠C=90°。若a=6，b=8，则
c= 。
2、在△ABC中，∠C=90°。若c=13，b=12，则
a= 。
3、若直角三角形中，有两边长是3和4，则第三
边长的平方为（ ）
A 25 B 14 C 7 D 7或25
10
5
D
实践应用二：探索情境
1、某楼三楼失火，消防队员立即赶来救火了解到每层楼高3米,消防队员取来6.5米长的云梯，如果云梯的底部离墙基的距离是2.5米,试问消防队员能否进入三楼灭火 (flash)
实践应用二：探索情境
2、如图所示，一棵大树在一次强烈台风中于离地面9米处折断倒下，树顶落在离树根12米处。大树在折断之前高多
少？
实践应用二：探索情境
3、有一个长方形盒子，长、
宽、高分别为4厘米、3
厘米、12厘米，一根长
为13厘米的木棒能否放
入？为什么？
4
3
12
实践应用三：拓展提高
1、小明妈妈买来一部29英寸（74厘米）的电视机。小明量了电视机的荧屏后，发现荧屏只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你同意他的想法吗？
(582=3364 462=2116 74.032≈5480)
1
1
1、你这节课的主要收获是什么？
2、该定理揭示了哪一类三角形中的什么元
素之间的关系？
3、在探索和验证定理的过程中，我们运用
了哪些方法？
4、你最有兴趣的是什么？你有没有感到困
难的地方？
（五）回顾反思，提炼精华