1.1 探索勾股定理（2）

(共20张PPT)
1.1 （2）探索勾股定理
-证明勾股定理
读一读
我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.图1-1称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会（TCM－2002）的会标，其图案正是“弦图”，它标志着中国古代的数学成就.
　　　　　　　
图1-1
图1-2
请同学们画四个与右图全等的直角三角形，并把它剪下来。
∟
a
b
c
用这四个三角形拼一拼、摆一摆，看看是否得到一个含有以斜边c为边长的正方形，你能利用它说明勾股定理吗？并与同伴交流。
c
a
b
c
a
b
c
a
b
c
a
b
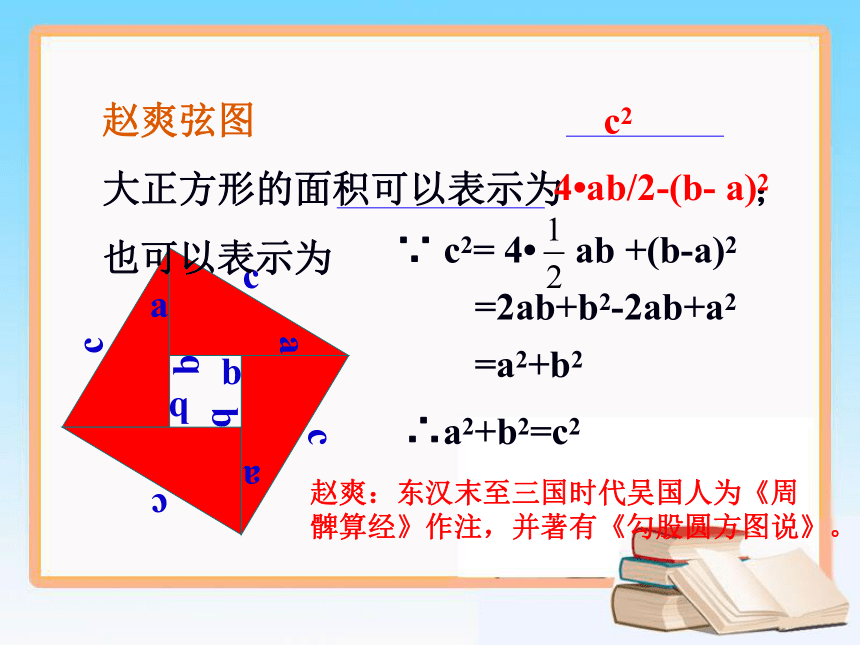
∵ c2= 4 ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
赵爽弦图
大正方形的面积可以表示为 ；
也可以表示为
c2
4 ab/2-(b- a)2
赵爽：东汉末至三国时代吴国人为《周
髀算经》作注，并著有《勾股圆方图说》。
c
a
b
c
a
b
c
a
b
c
a
b
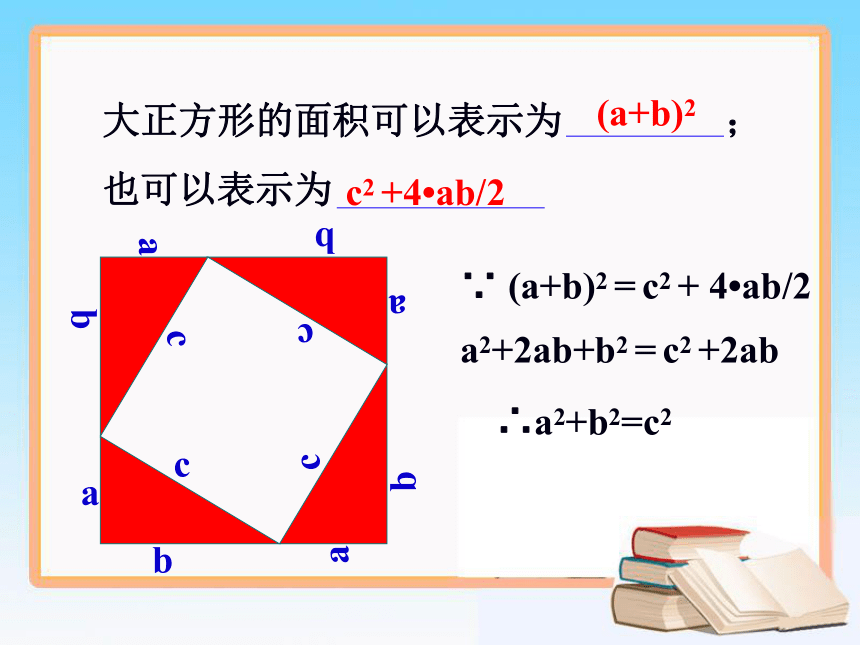
∵ (a+b)2 = c2 + 4 ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ；
也可以表示为
(a+b)2
c2 +4 ab/2
在1876年一个周末的傍晚，在美国首都 华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景……他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨．由于好奇心驱使他循声向两个小孩走去，想搞清楚两个小孩到底在干什么．只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形……
勾股定理的
于是这位中年人不再散步，立即回家，潜心探讨小男孩给他留下的难题。他经过反复的思考与演算，终于弄清楚了其中的道理，并给出了简洁的证明方法。 1876年4月1日，他在《新英格兰教育日志》上发表了他对勾股定理的这一证法。 1881年，这位中年人—伽菲尔德就任美国第二十任总统。后来，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为“总统”证法。
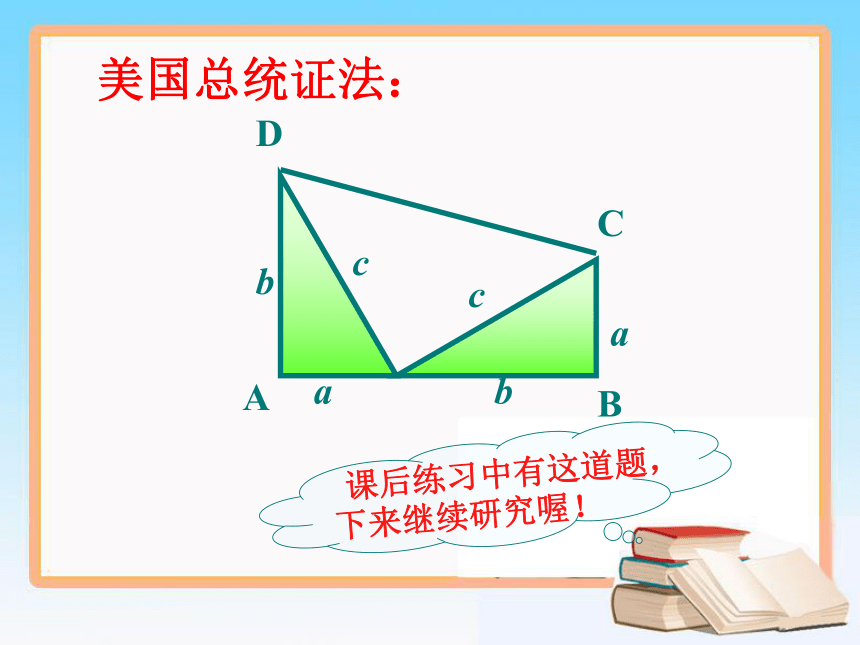
美国总统证法：
b
c
a
b
c
a
A
B
C
D
课后练习中有这道题，下来继续研究喔！
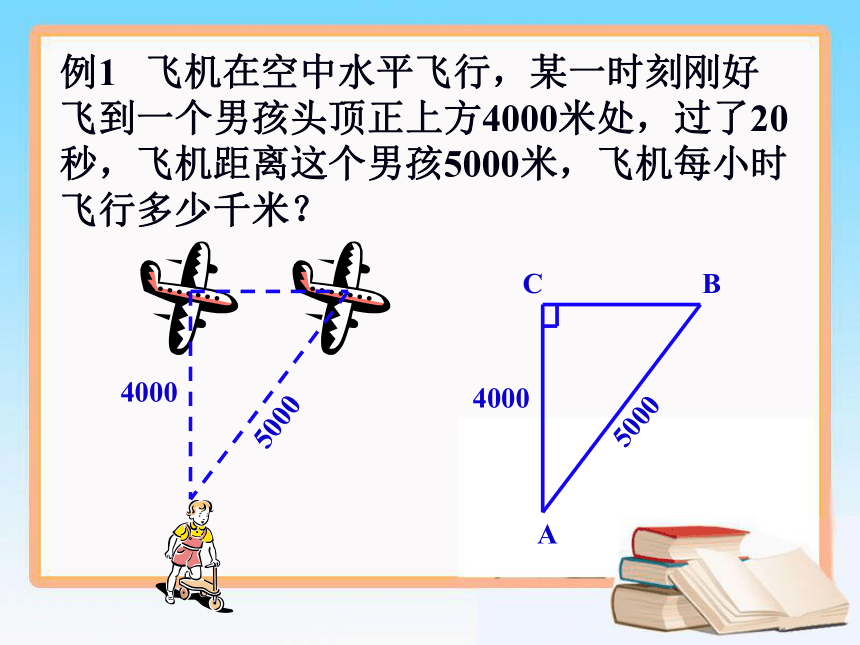
例1 飞机在空中水平飞行，某一时刻刚好飞到一个男孩头顶正上方4000米处，过了20秒，飞机距离这个男孩5000米，飞机每小时飞行多少千米？
4000
5000
5000
4000
C
B
A
D
A
B
C
例2 蚂蚁沿图中的折线从A点爬到D点，一共爬了多少厘米？（小方格的边长为1厘米）
G
F
E
1 、下列阴影部分是一个正方形，求此正方形的面积
15厘米
17厘米
解：设正方形的边长为x厘米 , 则
x2=172-152
x2=64
答：正方形的面积是64平方厘米。
练一练
2、如图，一根旗杆在离地面9米处断裂，旗杆顶部落在离旗杆底部12米处，旗杆折断之前有多高？
9米
12米
练一练
拓展练习
3、如图，受台风麦莎影响，一棵高18m的大树断裂，树的顶部落在离树根底部6米处，这棵树折断后有多高？
6米
补充练习：
1、放学以后，小红和小颖从学校分手，分别沿着东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖用20分钟到家，小红和小颖家的距离为 （ ）
A、600米； B、800米； C、1000米； D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米，那么斜边上的高是 （ ）
A、6厘米； B、 8厘米； C、 80/13厘米；D、 60/13厘米；
C
D
3、等腰三角形底边上的高为8，周长为32，求这个三角形的面积
8
X
16-X
D
A
B
C
解：设这个三角形为ABC，高为AD，设BD为X，则AB为（16-X），
由勾股定理得：
X2+82=(16-X)2
即X2+64=256-32X+X2
∴ X=6
∴ S ABC=BC AD/2=2 6 8/2=48
C
80
60
25
24
B
A
4. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
课堂练习： 一、判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( ) 2. ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=9,b=40,则c=______. 2.在 ABC中, C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边为上的高为______.

6
8
41

24
4.8
小结
1、本节课学习了直角三角形的哪些知识？
2、通过这节课的学习，你在解题思路和方法上有什么收获？
作业：1、P9的习题1.2
2、补充作业：
(1) 上网查有关勾股定理的历史资料
（2） 一轮船以16海里/小时的速度离A港向东北方向航行，另一艘轮船同时以12海里/小时的速度离A港向西北方向航行，2小时后，两船相距多少海里？
（3）如图在△ABC中，∠ACB=90 ， CD⊥AB，D为垂足，AC=2.1cm,BC=2.8cm.
求① △ABC的面积；
②斜边AB的长；
③斜边AB上的高CD的长。
D
A
B
C