1.1《平行四边形及其性质》(2)

(共13张PPT)
九年级数学(上)第一章：特殊四边形
掌握平行四边形对角线的性质，会用此性质进行有关的论证和计算.进一步 培养演绎推理能力和发散思维能力；
学习目标
1、什么叫平行四边形？如何表示
2、平行四边形有哪些性质定理
3、如何用几何语言表述它的性质定理？
导入新课
一天，财主巴依遇到阿凡提，想考一考聪明的阿凡提，说给你两块地，一块是平行四边形形状的（如下图，AB=10，OA=3，BC=8），还有一块是边长是7的正方形EFGH土地，让你来选一下，哪一块面积更大？
7
G
F
E
H
O
C
B
A
D
请同学们认真阅读课本第6页和第7页，完成以下内容：
1、平行四边形的第3个性质定理是什么？你会证明吗？
2、怎样运用平行四边形的性质定理进行证明？
A　
B　
C　
D　
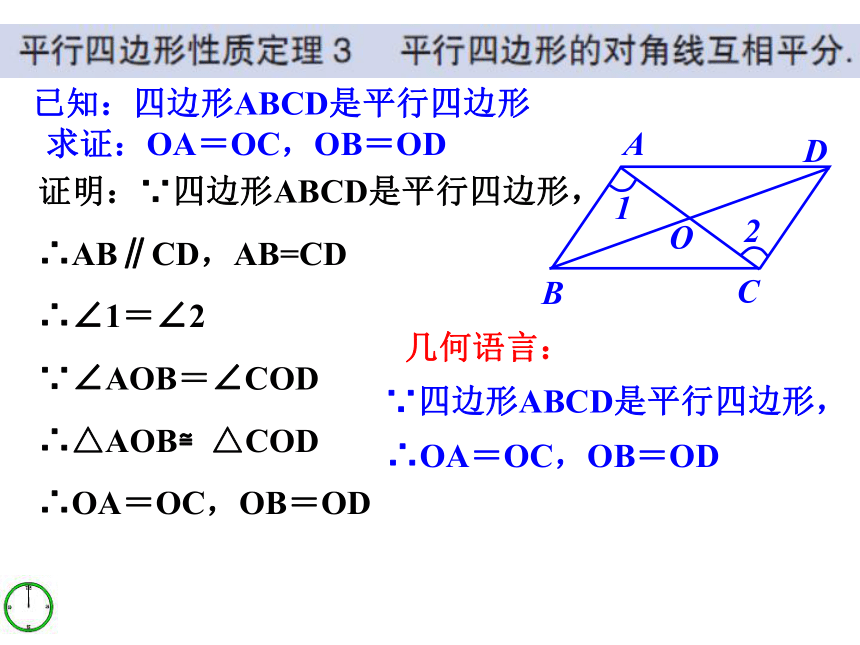
证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD
O　
∴∠1＝∠2
1　
2　
∵∠AOB＝∠COD
∴△AOB≌△COD
∴OA＝OC，OB＝OD
几何语言：
∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD
已知：四边形ABCD是平行四边形
求证：OA＝OC，OB＝OD
例1.如图，在平行四边形ABCD中，对角线AC和BD相交于点O，△AOB的周长为15，AB＝6，那么对角线AC与BD的和是多少
在平行四边形ABCD中，
已知AB＝6，
AO+BO+AB＝15，
∴　AO+BO＝15-6＝9．
又∵　AO＝OC， BO＝OD(平行四边形对角线互相平分)，
∴　AC+BD＝2AO+2BO＝2(AO+BO)＝２×９＝18．
能力立意：利用整体思想.
拓展提升：
运用代数方法解决几何问题
　　　□ABCD的周长为60cm，对角线交于点O，△AOB的周长比△BOC的周长大8cm，求AB，BC的长．
【答案】四边形ABCD是平行四边
形．∴AB=CD，AD=BC，AO=CO，
∵ABCD的周长是60．∴2AB+2BC=60，
即AB+BC=30，①
又∵△AOB的周长比△BOC的周长大8．
即（AO+OB+AB）-（BO+OC+BC）=
AB-BC=8， ②
由①②得
∴AB，BC的长分别是19cm和11cm．
规律方法总结
本题是根据平行四边形的对边相等，对角线互相平分的性质来解的．运用代数方法解决几何问题是常用的数学方法．
课堂小结：
1、平行四边形有哪些性质？
2、这些性质的几何语言是什么？
作业