1.3特殊的平行四边形(1)

(共28张PPT)
九年级数学(上)第一章：特殊四边形
同学们，我们在小学已学过长方形，你能找出我们身边的长方形吗？思考长方形有哪些性质？
导入新课
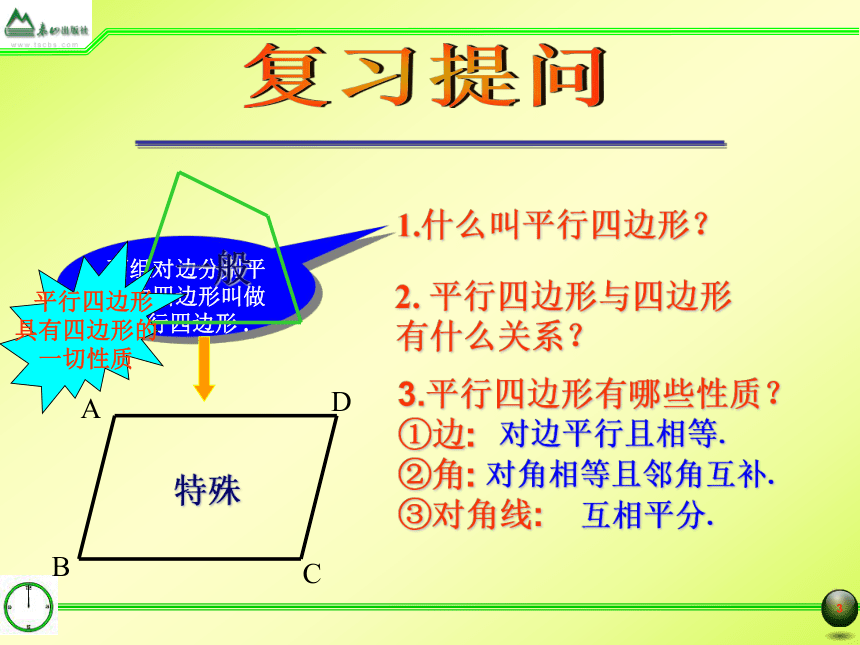
1.什么叫平行四边形？
3.平行四边形有哪些性质？
①边:
②角:
③对角线:
A
B
C
D
两组对边分别平行的四边形叫做平行四边形 .
特殊
一般
2. 平行四边形与四边形 有什么关系？
平行四边形
具有四边形的
一切性质
对边平行且相等.
对角相等且邻角互补.
互相平分.
阅读课文第13页到第15页，思考以下问题：
1、什么叫矩形？
2、矩形有哪些性质定理和推论？
3、矩形有哪些判定定理？
α
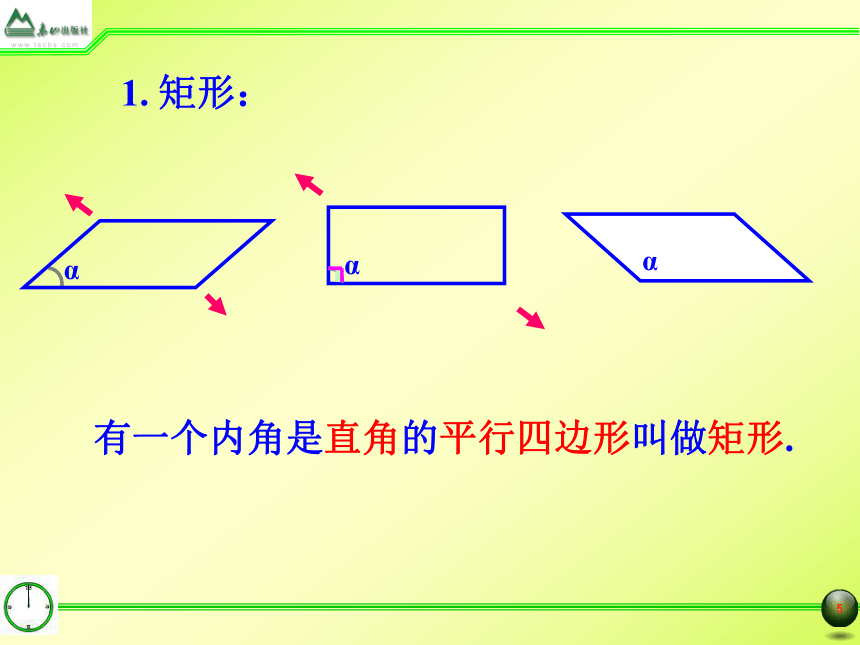
1. 矩形：
α
α
有一个内角是直角的平行四边形叫做矩形.
思考2：如果把“平行四边形”换成“四边形”或去掉“有一个角是直角”能保证是矩形吗？
【答案】不能保证，矩形需具备两个条件（1）有一个角是直角；（2）平行四边形，缺一不可．
思考3：矩形是轴对称图形码？
有几条对称轴？
【答案】是；有两条对称轴．
思考4：将上图的矩形对折，观察、猜想 、矩形的四个角都是直角吗？为什么？你能用逻辑推理的方法证明吗？
【答案】是．
已知：矩形ABCD中，设∠D=90°，
求证：∠A= ∠B= ∠C= 90°．
证明：如图，矩形ABCD中，设∠D=90°，
∵四边形ABCD为矩形，
∴四边形ABCD也是平行四边形．
∴ ∠D= ∠Ｂ=90°．(平行四边形的对角相等）
又∵AD//BC，
∴∠C= 180 ° － 90° =90°．
∴ ∠A= ∠C= 90°．（平行四边形的对角相等）
∴ ∠A= ∠B= ∠C= ∠D= 90°．
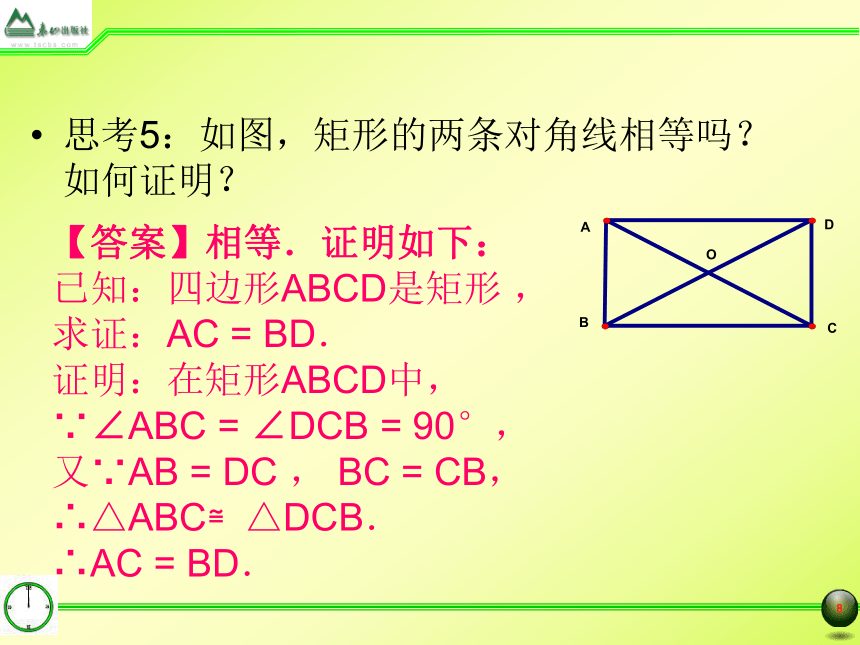
思考5：如图，矩形的两条对角线相等吗？如何证明？
【答案】相等．证明如下：　已知：四边形ABCD是矩形 ，求证：AC = BD．
证明：在矩形ABCD中，
∵∠ABC = ∠DCB = 90°，
又∵AB = DC ， BC = CB，
∴△ABC≌△DCB．
∴AC = BD．
归纳总结：
(1)矩形的概念：有一个角是直角的平行四边 形是矩形.
(2)矩形特有的性质：矩形的四个角是直角
矩形的对角线相等.
探究点二：直角三角形的性质
思考1：如图，在任意的矩形ABCD中，AC，BD相交于O，那么BO与AC有怎样的数量关系？
【答案】BO= AC．
思考2：如图，Rt△ABC中，
BO是一条什么线？ 由此你能得到什么结论？
【答案】 Rt△ABC中，BO是斜边AC上的中线，所以直角三角形斜边上的中线等于斜边的一半．
直角三角形的性质：直角三角形斜边上的中线等于斜边的一半.此性质需要具备两个条件:(1)在直角三角形中；(2)斜边的中线. 缺一不可.
归纳总结
2. 矩形的性质：
矩形的性质定理1：矩形的四个角都是直角.
A
D
C
B
矩形的性质定理2：矩形的两条对角线相等.
O
性质定理的推论：直角三角形斜边上的中线
　　　　　　　　等于斜边长的一半.
(二)知识综合应用探究
探究点一：矩形性质的应用（重点）
例1：已知如图，矩形ABCD的两条对角线相交于点Ｏ，∠AOD=120°， AB = 4cm．
（1）求矩形对角线的长；
（2）求BC边的长 ．
思考：∠AOD=120°，由矩形对角线的性质可知△AOB 是什么三角形？
【答案】 △AOB 是等边三角形．
思考：△ABC是什么三角形？利用什么方法求BC？
【答案】 △ABC是直角三角形，利用勾股定理可求BC．
拓展提升
已知：如图 ，矩形 ABCD中，AB长8 cm ，对角线比AD边长4 cm．求AD的长及点A到BD的距离AE的长．
分析：（1）因为矩形四个角都是直角，因此△ABD是直角三角形，若设AD=ｘcm，则对角线BD=（ｘ+4）cm，由勾股定理得64+ｘ2=(ｘ+4)2,解得ｘ=6 cm．
（2）利用直角三角形面积公式，可得到两直角边、斜边及斜边上的高的一个基本关系式： AE×BD＝ AD×AB，即AE ×10=6×8, ∴AE=4.8cm．
规律方法总结
解决矩形的问题，一般常用到勾股定理，
还要灵活应用矩形的性质等．
探究点二：直角三角形的性质
例2：已知：如图，BD、CE是△ABC的两条高，M是BC的中点，
求证：ME=MD．
思考1：图中有哪些直角三角形？
【答案】 Rt△BDC ; Rt△BEC;
Rt△AEC ; Rt△ABD．
思考2：在直角三角形中有中点你想到了什么
【答案】直角三角形斜边的中线等于斜边的一半 ．
规律方法总结
1．在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角是30°.
2．解决有关矩形的题目，首先要注意挖掘矩形本身具有的性质，挖掘题目中的隐含条件，矩形性质经常与直角三角形的有关性质结合起来解决线段或角的问题，注意转化的数学思想在解题中的应用．
总结升华
【课堂小结】
本节主要学习了矩形的性质和直角三角形的重要性质， 矩形性质经常与直角三角形的有关性质结合起来解决线段或角的问题，注意转化的数学思想在解题中的应用．
目标检测:
解:
已知 的两条对角线AC、BD相交于点O，△AOB是等边三角形, 求∠BAD的度数.
ABCD
A
D
C
B
O
∴AC=BD
如图,
△AOB是等边三角形,
所以 OA=OB.
∵ 的对角线互相平分,
ABCD
因此 是矩形.
ABCD
∴ ∠BAD=900 .
∴AC=2AO,BD=2BO.
随堂练习
主要内容：
1、矩形的定义：
有一个角是直角的平行四边形叫矩形　
2、矩形的性质：
矩形的对边平行且相等.
矩形的四个角都是直角.
矩形的两条对角线相等
且互相平分.
矩形是轴对称图形.
直角三角形斜边上的中线等于斜边长的一半.
(2).矩形的两条对角线将矩形分成四个面积相等的
等腰三角形( )
(1).矩形是平行四边形( )
练一练
矩形的短边长为3cm,两对角线所成的钝角是120 °,
则它的对角线长是_______.
2. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.
6cm
cm
3.判断题
作业