沪科教 课标版_选修3-5_1.3动量守恒定律的案例 课件20张PPT
文档属性
| 名称 | 沪科教 课标版_选修3-5_1.3动量守恒定律的案例 课件20张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 489.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-25 11:05:50 | ||
图片预览








文档简介
6.2动量守恒定律及应用
一、基本概念
动量守恒定律内容:一个系统不受外力或所受外力之和为零,这个系统的总动量保持不变,这个结论叫做动量守恒定律。
1、系统与个体
系统:几个相互作用的物体系
个体:单独一个物体
2、内力与外力
内力:系统内物体间的力
外力:系统外给系统的力
3、适用条件:
(1)系统不受外力或系统所受的外力的合力为零。
(2)系统所受外力的合力虽不为零,但比系统内力小得多。
(3)系统所受外力的合力虽不为零,但在某个方向上的分力为零,则在该方向上系统的总动量保持不变——分动量守恒。
4、动量守恒定律的四性:
1.矢量性:动量守恒方程是一个矢量方程,对于作用前后物体的运动方向都在同一直线上的问题,应选取统一的正方向。凡是与选取的正方向相同的为正,相反为负。若方向未知,可设为与正方向相同来列动量守恒方程,通过解的结果的正负,判定未知量的方向。
2.瞬时性:动量是一个瞬时量,动量守恒是指系统在任一瞬时的动量守恒。m1v1+m2v2=m1v1′+m2v2′,等号左边是作用前的各物体动量和,等号右边是作用后的各物体动量和,不同时刻动量不能相加。
3.相对性:动量大小与选择的参考系有关,应注意各物体的速度是相对同一惯性系的速度,一般选取地面为参考系。
4.普适性:它不仅适用于两个物体组成的系统,也适用于多个物体组成的系统;不仅适用于宏观物体组成的系统,也适用于微观粒子组成的系统。
5、动量守恒的数学表述形式:
(1)p=p′. 即系统相互作用开始时的总动量等于相互作用结束时(或某一中间状态时)的总动量;
(2)Δp=0. 即系统的总动量的变化为零.若所研究的系统由两个物体组成,则可表述为:
m1v1+m2v2=m1v1′+m2v2′(等式两边均为矢量和)
(3)Δp1=-Δp2. 即若系统由两个物体组成,则两个物体的动量变化大小相等,方向相反,此处要注意动量变化的矢量性.在两物体相互作用的过程中,也可能两物体的动量都增大,也可能都减小,但其矢量和不变.
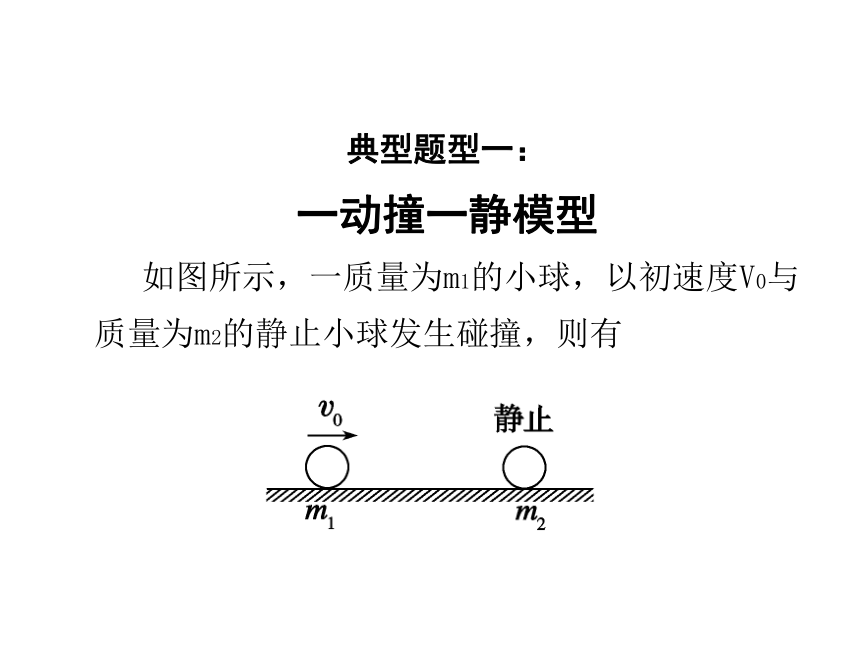
典型题型一:
一动撞一静模型
如图所示,一质量为m1的小球,以初速度V0与质量为m2的静止小球发生碰撞,则有
动量守恒:m1V0=m1V1+m2V2
机械能守恒:
联立可得:
(1)当m1>m2,
(4)当m1》m2,
(2)当m1=m2,
(3)当m1(5)当m1《m2,
1、弹性碰撞——无机械能损失
2、非弹性碰撞——有机械能损失
动量守恒: m1V0=m1V1+m2V2
功能关系:
3、完全非弹性碰撞——机械能损失最大
注:标志性语言“碰撞后粘在一起”
——即,碰撞后达到“共速”
动量守恒:m1V0=(m1+m2)V共
功能关系:
此时的?E损为碰撞过程中损失机械能的最大值
典型题型二:
子弹打物块模型
一、牛顿第二定律角度:
m:f=ma1,V共=V0-a1t
M:f=Ma2,V共=a2t
二、功能关系角度:
m:
M:
将两方程相加,我们能得出
即:fX相=Q…………①
三、动量关系:
mV0=(M+m)V共………②
总结:
1、未穿出的情况下,我们在解决问题时候通常都是利用一个能量方程和一个动量方程做结合,即:
方程①与方程②结合
2、穿出的情况下(即子弹与物块最终不共速),动量关系方程将变成:mV0=mV1+MV2……3
功能关系有一特殊地方,由于穿出是的相对位移恒等于物块的长度,所以机械能损失量将是定值,为:
Q=f×L (L为物块的长度)…………4
注:在实际操作中,子弹打物块的过程中的 X物块极小,可以忽略
即:我们将子弹打物块的过程分为两个过程
过程一、子弹打进物块过程中,物块不动
过程二、子弹进入到与物块“相对静止”的位置后,子弹与物块共同以某一速度向前运动
下面我们来看一个对应训练
光滑水平面上,放置着两个质量均为M的物块A和B,其间用以轻质弹簧相连接,一质量为m的子弹以V0的初速度打入A物块中,未穿出,求在整个过程中的弹性势能的最大值Ep
分析:
解决问题:
过程一、子弹与A物块作用
mV0=(m+M)V1
过程二、子弹和A物块与B物块作用
(m+M)V1=(m+2M)V共
由于过程一中A物块不动,弹簧不被压缩,则弹性势能只产生于过程二中,即过程二中的动能损失将全部转化为弹性势能,则有,
变式训练
一质量为m可视为质点的小物块,以速度V0冲上一质量为M的长木板,物块与木板之间的动摩擦因数为μ,木板与地面间光滑,若物块未滑出木板,求物块在木板上滑行的距离
mV0=(m+M)V共
解得X相=
注:另一种问法,若要小物块恰好不从模板边缘滑下,则模板至少要多长?
这时满足的条件为:X相=模板长度L 即可
即
典型题型三
人船模型
一质量为m的人站在质量为M,长为L的船左侧,忽略水的阻力,当人走至船右侧时,人和船各走多远?
总动量是0,则当人动的时候,船也得动,并且二者的动量等大反向,
即:mV人=MV船,
又V人=X人/t,V船=X船/t
则有,mX人=MX船
且, X人+X船=L
可解得
一、基本概念
动量守恒定律内容:一个系统不受外力或所受外力之和为零,这个系统的总动量保持不变,这个结论叫做动量守恒定律。
1、系统与个体
系统:几个相互作用的物体系
个体:单独一个物体
2、内力与外力
内力:系统内物体间的力
外力:系统外给系统的力
3、适用条件:
(1)系统不受外力或系统所受的外力的合力为零。
(2)系统所受外力的合力虽不为零,但比系统内力小得多。
(3)系统所受外力的合力虽不为零,但在某个方向上的分力为零,则在该方向上系统的总动量保持不变——分动量守恒。
4、动量守恒定律的四性:
1.矢量性:动量守恒方程是一个矢量方程,对于作用前后物体的运动方向都在同一直线上的问题,应选取统一的正方向。凡是与选取的正方向相同的为正,相反为负。若方向未知,可设为与正方向相同来列动量守恒方程,通过解的结果的正负,判定未知量的方向。
2.瞬时性:动量是一个瞬时量,动量守恒是指系统在任一瞬时的动量守恒。m1v1+m2v2=m1v1′+m2v2′,等号左边是作用前的各物体动量和,等号右边是作用后的各物体动量和,不同时刻动量不能相加。
3.相对性:动量大小与选择的参考系有关,应注意各物体的速度是相对同一惯性系的速度,一般选取地面为参考系。
4.普适性:它不仅适用于两个物体组成的系统,也适用于多个物体组成的系统;不仅适用于宏观物体组成的系统,也适用于微观粒子组成的系统。
5、动量守恒的数学表述形式:
(1)p=p′. 即系统相互作用开始时的总动量等于相互作用结束时(或某一中间状态时)的总动量;
(2)Δp=0. 即系统的总动量的变化为零.若所研究的系统由两个物体组成,则可表述为:
m1v1+m2v2=m1v1′+m2v2′(等式两边均为矢量和)
(3)Δp1=-Δp2. 即若系统由两个物体组成,则两个物体的动量变化大小相等,方向相反,此处要注意动量变化的矢量性.在两物体相互作用的过程中,也可能两物体的动量都增大,也可能都减小,但其矢量和不变.
典型题型一:
一动撞一静模型
如图所示,一质量为m1的小球,以初速度V0与质量为m2的静止小球发生碰撞,则有
动量守恒:m1V0=m1V1+m2V2
机械能守恒:
联立可得:
(1)当m1>m2,
(4)当m1》m2,
(2)当m1=m2,
(3)当m1
1、弹性碰撞——无机械能损失
2、非弹性碰撞——有机械能损失
动量守恒: m1V0=m1V1+m2V2
功能关系:
3、完全非弹性碰撞——机械能损失最大
注:标志性语言“碰撞后粘在一起”
——即,碰撞后达到“共速”
动量守恒:m1V0=(m1+m2)V共
功能关系:
此时的?E损为碰撞过程中损失机械能的最大值
典型题型二:
子弹打物块模型
一、牛顿第二定律角度:
m:f=ma1,V共=V0-a1t
M:f=Ma2,V共=a2t
二、功能关系角度:
m:
M:
将两方程相加,我们能得出
即:fX相=Q…………①
三、动量关系:
mV0=(M+m)V共………②
总结:
1、未穿出的情况下,我们在解决问题时候通常都是利用一个能量方程和一个动量方程做结合,即:
方程①与方程②结合
2、穿出的情况下(即子弹与物块最终不共速),动量关系方程将变成:mV0=mV1+MV2……3
功能关系有一特殊地方,由于穿出是的相对位移恒等于物块的长度,所以机械能损失量将是定值,为:
Q=f×L (L为物块的长度)…………4
注:在实际操作中,子弹打物块的过程中的 X物块极小,可以忽略
即:我们将子弹打物块的过程分为两个过程
过程一、子弹打进物块过程中,物块不动
过程二、子弹进入到与物块“相对静止”的位置后,子弹与物块共同以某一速度向前运动
下面我们来看一个对应训练
光滑水平面上,放置着两个质量均为M的物块A和B,其间用以轻质弹簧相连接,一质量为m的子弹以V0的初速度打入A物块中,未穿出,求在整个过程中的弹性势能的最大值Ep
分析:
解决问题:
过程一、子弹与A物块作用
mV0=(m+M)V1
过程二、子弹和A物块与B物块作用
(m+M)V1=(m+2M)V共
由于过程一中A物块不动,弹簧不被压缩,则弹性势能只产生于过程二中,即过程二中的动能损失将全部转化为弹性势能,则有,
变式训练
一质量为m可视为质点的小物块,以速度V0冲上一质量为M的长木板,物块与木板之间的动摩擦因数为μ,木板与地面间光滑,若物块未滑出木板,求物块在木板上滑行的距离
mV0=(m+M)V共
解得X相=
注:另一种问法,若要小物块恰好不从模板边缘滑下,则模板至少要多长?
这时满足的条件为:X相=模板长度L 即可
即
典型题型三
人船模型
一质量为m的人站在质量为M,长为L的船左侧,忽略水的阻力,当人走至船右侧时,人和船各走多远?
总动量是0,则当人动的时候,船也得动,并且二者的动量等大反向,
即:mV人=MV船,
又V人=X人/t,V船=X船/t
则有,mX人=MX船
且, X人+X船=L
可解得
同课章节目录
