人教版小学数学六年级下册小升初复习讲义7分数应用题
文档属性
| 名称 | 人教版小学数学六年级下册小升初复习讲义7分数应用题 |

|
|
| 格式 | docx | ||
| 文件大小 | 165.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览



文档简介
分数应用题
学生姓名
年级
学科
授课教师
日期
时段
核心内容
解决复杂分数应用题
课型
一对一
教学目标
1、使学生学会掌握“已知一个数,求它的几分之几和比它多(或少)几分之几的数是多 少”及"已知一个数的几分之几和比它多(或少)几分之几数是多少,求这个数””的应用题的解答方法,并能熟练地列方程解答这类应用题。
2、进一步培养学生自主探索解决问题的能力和加强分析、推理和判断等思维能力,提高解答应用题的能力。
重、难点
重点:弄清单位“1”的量,会分析题中的数量关系。掌握常用的解决稍复杂分数应用题的技巧
难点:灵活运用技巧解决分数应用题
2532380114935
课首沟通
1、上次的作业完成了没有?有不会的题吗?
2、你会解答哪些类型的分数乘除应用题,举例说明?
3、如何理解“量率”对应关系?画线段图分析题意,什么情况画单线段图?什么情况画双线段图?
课首小测
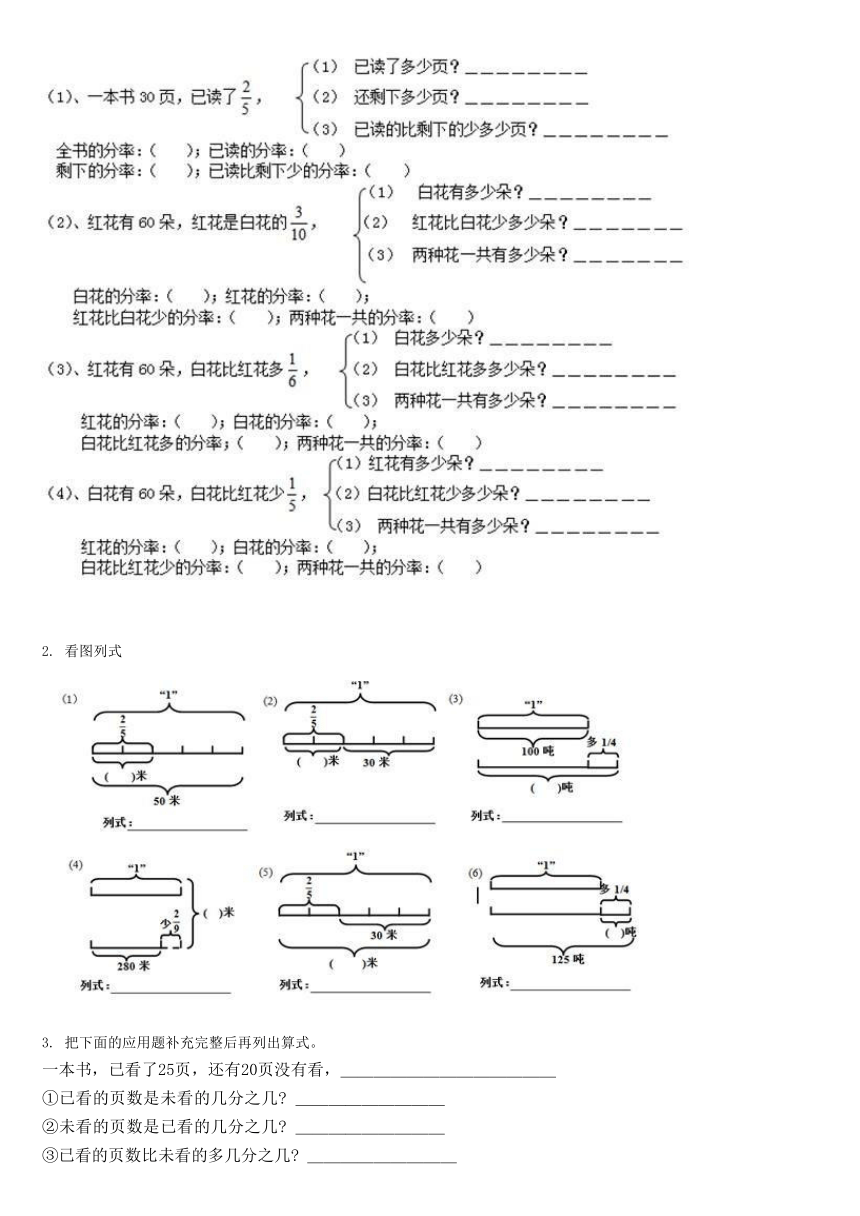
先找出对应分率,再列式,不用计算。
看图列式
516255177165
把下面的应用题补充完整后再列出算式。
一本书,已看了25页,还有20页没有看,_____________
①已看的页数是未看的几分之几? _________
②未看的页数是已看的几分之几? _________
③已看的页数比未看的多几分之几? _________
④未看的页数比已看的少几分之几? _________
⑤已看的页数是全书的几分之几? _________
⑥未看的页数是全书的几分之几? _________
(大联盟试题)) 工程队用3天修完一段路,第一天修的是第二天的,第三天修的是第二天的倍,已知第三天比第一天多修270米,这段路长多少米?
(大联盟试题)) 某工程队修一条路,第一天修了比全长的多2米,第二天修了比剩下的少4米,还剩下200米没有修,这段路全长多少米?
(小联盟试题)) 有一些数字卡片,上面写的数全部都是3或4的倍数,其中是3的倍数的卡片占
,是4的倍数的卡片占 ,12的倍数的卡片有20张,求一共有多少张卡片.
2532380251460
知识梳理
解答分数应用题,首先要确定单位“1”,在单位“1”确定以后,一个具体数量总与一个具体分数
(分率)相对应,这种关系叫“量率对应”,这是解答分数应用题的关键。 1、分数乘法应用题:
①意义:是指已知一个数,求它的几分之几及比它多(或少)几分之几的数是多少的应用题。
②特征:已知单位“1”的量和分率,求与分率所对应的实际数量。
③数量关系式:单位“1”×分率=对应数量
或单位“1”×(1±分率)=对应数量2、分数除法应用题:
求分率
①意义:求一个数是另一个数的几分之几及比它多(或少)几分之几是多少的应用题。
②特征:已知一个数和另一个数,求一个数是另一个数的几分之几及比它多(或少)几分之几的数,“一个数”是比较量,“另一个数”是标准量。求分率,也就是求他们的倍数关系。
③数量关系式:(甲数-乙数)/乙数
或(甲数-乙数)/甲数 。
求具体量
①意义:已知一个数的几分之几及比它多(或少)几分之几数是多少,求这个数。
②特征:已知一个实际数量和它相对应的分率,求单位“1”的量。
③数量关系式:对应数量÷分率=单位“1”的量
或对应数量÷(1±分率)=单位“1”的量
导学一 : 利用假设法找出解题方法
知识点讲解 1
分数应用题中有一个“量率对应”的明显特点,对一个单位“1”来说,每个分率都对应着一个具体的数量,而每一个具体的数量,也同样对应着一个分率,因此,正确地确定“量率对应”是解题的关键。
例 1. 红花村修一条水渠,第一周修了全长的多10米,第二周修了全长的 少5米,还剩下282 米没有修。这条水渠长多少米?
【学有所获】(1)做此类题我们先找 ;再判断 ;最后要 ; (2)当一题中出现分数和数量不对应时,我们使 .
导学二 : 通过转化单位“1”找出解题方法
知识点讲解 1
在一道分数应用题中,如果出现了几个分率,而且这些分率的标准量不同,量的性质相异,在解题时,必须以题中的某 一个量为标准量,将其余量的对应分率统一到这个标准量上来,才可列式解答。
例 1. 果园里有苹果树和梨树共420棵,苹果树棵数的等于梨树的 ,问这两种果树各有多少棵?
【学有所获】(1)做此类题我们先找 ;再判断 ;再转化 ;最后要
;
(2)当一题中出现分数单位“1”不统一时,我们要 .
导学三 : 通过逆推找出解题方法
知识点讲解 1
有些分数应用题,如果按从始至终的先后顺序去分析,很难达到应用题的目的,甚至陷入绝境。不妨“反过来想一想”进行逆推,便容易打开思路,顺利解题。
2837815-215905751830-21590例 1. 有一个油桶里的油,第一次倒出 后加入20千克,第二次倒出这时油的 多5千克,这时桶里剩下油95千克。问原来桶里有油多少千克?
导学四 : 抓住不变量找出解题方法
知识点讲解 1
对于标准量不统一的分数应用题,如果我们能从题中找到一个不变量,就以不变量为突破口,便能够很快找到解题方法。
3060065-21590812165477520例 1. 一个车间有工人360人,其中女工占 ,后来又招进一批女工,这时女工人数占全车间工人总人数的 ,又招进女工多少人?
导学五 : 借助线段图找出解题方法
知识点讲解 1
分数应用题的数量关系比较抽象、隐蔽,如果根据题意画出线段图,可使抽象变具体,隐蔽明朗化,从而借助线段图揭示的数量关系可直观地找出解题方法,甚至有的题还可找到简捷的解法。
例 1. 甲乙两人共存人民币若干元,其中甲占,若乙给甲60元后,则乙余下的钱占总数的 ,甲乙两人各存人民币多少元?
我爱展示
某人看一本书,第一天看的比总页数的 多4页,第二天看的比剩下的 少10页,结果还剩62页没看,这本书共有多少页?
甲乙二人各有玻璃球若班干个,拿出甲的 给乙后,乙再拿出它的 给甲,这时甲乙二人分别有玻璃球26个和20个,求甲乙二人原来各有多少个玻璃球?
某校六年级有学生152人,选出男生的 和5名女生参加竞赛,剩下的男生和女生人数相等,参加竞赛的有多少人?
张师傅三天生产一批零件,第一天生产了总数的 ,第二天生产了150个,第三天生产的个数是前两天之和的 。这批零件共有多少个?
某居民小区内,槐树的棵数占所有树木总数的40%。今年为了改善环境,又栽种了50棵槐树,这样使得槐树的棵数占全部树木总棵数的 。这个小区内原来一共有树木多少棵?
甲、乙两班的人数相等,各有一些同学参加课外天文小组,甲班参加天文小组的人数恰好是乙班没有 参加的人数的 ,乙班参加天文小组的人数是甲班没有参加人数的 。甲班没有参加的人数是乙班没有参加人数的几分之几?
2532380249555
我当小老师
本堂课所学的知识有哪些?(口述) 你最喜欢的方法是什么,列举一道题说明,最难的题型是什么?
课后作业
一桶油20千克,用去一些后还剩下 。用去多少千克?
师徒两人共同加工一批零件,3天完成了 ,已知师傅独做需要20天完成。徒弟独做需要多少天完成?
3087370-75565一辆汽车从甲地去乙地,已行了全程的 ,这时距中点还有15千米。已行了多少千米?
邮递员往山区送报,去时每小时走 千米,走了 小时到达;到达后立即返回,这样往返一共用了1 小时。求邮递员返回时平均每小时走多少千米?
三家合用一捆电线,甲家用了全长的 ,正好是45米,乙、丙两家按7:8正好用完,乙、丙两家各用多少米?
有甲、乙两块长方形试验田,甲长40米,宽30米,乙长50米,宽60米,现把350千克化肥按面积进行分配,甲、乙试验田各应分到多少千克?
2532380224155
1、将本堂课错题本中的练习再做一遍。
2、你平时还遇到什么分数应用题是今天老师还没讲到的,请写在下面,下次课我们一起解决。
2532380217805
课首小测
1.(1) ; ; ;①30× ;②30× ;③30×
(2) 1 ; ; ; 1 );①60÷ ;②60÷ × ;③60÷ ×1
49377603790955307965379095(3)1 ; 1 ; ; 2 ;①60×1 ; ②60× ;③60×2 ;
(4)1 ; ; ; 1 ;①60÷ ; ②60÷ × ;③60÷ ×1
2421255-311152.(1)50× ;(2)30÷(1- )× ;(3)100×(1+ );
1699895-311154660265-31115(4)280+280÷(1- ) ;(5)30÷(1- );(6)125-125÷(1+ )
3.①25÷20; ②20÷25;③(25-20)÷20 ;
④(25-20)÷25; ⑤25÷(25+20); ⑥20÷(25+20)
4.2790米
5.826米
6.48张
导学一
知识点讲解 1 例题
7010402152651.820米
解析:
导学二
知识点讲解 1 例题
10896601784351.苹果树:240棵#梨树:180棵
解析:梨树: (棵)
苹果树:420-180=240(棵)
导学三
知识点讲解 1 例题
1.150千克
导学四
知识点讲解 1 例题
1.24人
导学五
知识点讲解 1 例题
1.甲:240元;乙:160元
我爱展示
1.244页
2.甲:30;乙:16
3.12人
4.600个
4972052413005.500棵
6.
课后作业
1.12千克
2.30天
3.60千米
4.10千米
5.乙63米;丙72米
6.甲:100千克#乙:250千克
学生姓名
年级
学科
授课教师
日期
时段
核心内容
解决复杂分数应用题
课型
一对一
教学目标
1、使学生学会掌握“已知一个数,求它的几分之几和比它多(或少)几分之几的数是多 少”及"已知一个数的几分之几和比它多(或少)几分之几数是多少,求这个数””的应用题的解答方法,并能熟练地列方程解答这类应用题。
2、进一步培养学生自主探索解决问题的能力和加强分析、推理和判断等思维能力,提高解答应用题的能力。
重、难点
重点:弄清单位“1”的量,会分析题中的数量关系。掌握常用的解决稍复杂分数应用题的技巧
难点:灵活运用技巧解决分数应用题
2532380114935
课首沟通
1、上次的作业完成了没有?有不会的题吗?
2、你会解答哪些类型的分数乘除应用题,举例说明?
3、如何理解“量率”对应关系?画线段图分析题意,什么情况画单线段图?什么情况画双线段图?
课首小测
先找出对应分率,再列式,不用计算。
看图列式
516255177165
把下面的应用题补充完整后再列出算式。
一本书,已看了25页,还有20页没有看,_____________
①已看的页数是未看的几分之几? _________
②未看的页数是已看的几分之几? _________
③已看的页数比未看的多几分之几? _________
④未看的页数比已看的少几分之几? _________
⑤已看的页数是全书的几分之几? _________
⑥未看的页数是全书的几分之几? _________
(大联盟试题)) 工程队用3天修完一段路,第一天修的是第二天的,第三天修的是第二天的倍,已知第三天比第一天多修270米,这段路长多少米?
(大联盟试题)) 某工程队修一条路,第一天修了比全长的多2米,第二天修了比剩下的少4米,还剩下200米没有修,这段路全长多少米?
(小联盟试题)) 有一些数字卡片,上面写的数全部都是3或4的倍数,其中是3的倍数的卡片占
,是4的倍数的卡片占 ,12的倍数的卡片有20张,求一共有多少张卡片.
2532380251460
知识梳理
解答分数应用题,首先要确定单位“1”,在单位“1”确定以后,一个具体数量总与一个具体分数
(分率)相对应,这种关系叫“量率对应”,这是解答分数应用题的关键。 1、分数乘法应用题:
①意义:是指已知一个数,求它的几分之几及比它多(或少)几分之几的数是多少的应用题。
②特征:已知单位“1”的量和分率,求与分率所对应的实际数量。
③数量关系式:单位“1”×分率=对应数量
或单位“1”×(1±分率)=对应数量2、分数除法应用题:
求分率
①意义:求一个数是另一个数的几分之几及比它多(或少)几分之几是多少的应用题。
②特征:已知一个数和另一个数,求一个数是另一个数的几分之几及比它多(或少)几分之几的数,“一个数”是比较量,“另一个数”是标准量。求分率,也就是求他们的倍数关系。
③数量关系式:(甲数-乙数)/乙数
或(甲数-乙数)/甲数 。
求具体量
①意义:已知一个数的几分之几及比它多(或少)几分之几数是多少,求这个数。
②特征:已知一个实际数量和它相对应的分率,求单位“1”的量。
③数量关系式:对应数量÷分率=单位“1”的量
或对应数量÷(1±分率)=单位“1”的量
导学一 : 利用假设法找出解题方法
知识点讲解 1
分数应用题中有一个“量率对应”的明显特点,对一个单位“1”来说,每个分率都对应着一个具体的数量,而每一个具体的数量,也同样对应着一个分率,因此,正确地确定“量率对应”是解题的关键。
例 1. 红花村修一条水渠,第一周修了全长的多10米,第二周修了全长的 少5米,还剩下282 米没有修。这条水渠长多少米?
【学有所获】(1)做此类题我们先找 ;再判断 ;最后要 ; (2)当一题中出现分数和数量不对应时,我们使 .
导学二 : 通过转化单位“1”找出解题方法
知识点讲解 1
在一道分数应用题中,如果出现了几个分率,而且这些分率的标准量不同,量的性质相异,在解题时,必须以题中的某 一个量为标准量,将其余量的对应分率统一到这个标准量上来,才可列式解答。
例 1. 果园里有苹果树和梨树共420棵,苹果树棵数的等于梨树的 ,问这两种果树各有多少棵?
【学有所获】(1)做此类题我们先找 ;再判断 ;再转化 ;最后要
;
(2)当一题中出现分数单位“1”不统一时,我们要 .
导学三 : 通过逆推找出解题方法
知识点讲解 1
有些分数应用题,如果按从始至终的先后顺序去分析,很难达到应用题的目的,甚至陷入绝境。不妨“反过来想一想”进行逆推,便容易打开思路,顺利解题。
2837815-215905751830-21590例 1. 有一个油桶里的油,第一次倒出 后加入20千克,第二次倒出这时油的 多5千克,这时桶里剩下油95千克。问原来桶里有油多少千克?
导学四 : 抓住不变量找出解题方法
知识点讲解 1
对于标准量不统一的分数应用题,如果我们能从题中找到一个不变量,就以不变量为突破口,便能够很快找到解题方法。
3060065-21590812165477520例 1. 一个车间有工人360人,其中女工占 ,后来又招进一批女工,这时女工人数占全车间工人总人数的 ,又招进女工多少人?
导学五 : 借助线段图找出解题方法
知识点讲解 1
分数应用题的数量关系比较抽象、隐蔽,如果根据题意画出线段图,可使抽象变具体,隐蔽明朗化,从而借助线段图揭示的数量关系可直观地找出解题方法,甚至有的题还可找到简捷的解法。
例 1. 甲乙两人共存人民币若干元,其中甲占,若乙给甲60元后,则乙余下的钱占总数的 ,甲乙两人各存人民币多少元?
我爱展示
某人看一本书,第一天看的比总页数的 多4页,第二天看的比剩下的 少10页,结果还剩62页没看,这本书共有多少页?
甲乙二人各有玻璃球若班干个,拿出甲的 给乙后,乙再拿出它的 给甲,这时甲乙二人分别有玻璃球26个和20个,求甲乙二人原来各有多少个玻璃球?
某校六年级有学生152人,选出男生的 和5名女生参加竞赛,剩下的男生和女生人数相等,参加竞赛的有多少人?
张师傅三天生产一批零件,第一天生产了总数的 ,第二天生产了150个,第三天生产的个数是前两天之和的 。这批零件共有多少个?
某居民小区内,槐树的棵数占所有树木总数的40%。今年为了改善环境,又栽种了50棵槐树,这样使得槐树的棵数占全部树木总棵数的 。这个小区内原来一共有树木多少棵?
甲、乙两班的人数相等,各有一些同学参加课外天文小组,甲班参加天文小组的人数恰好是乙班没有 参加的人数的 ,乙班参加天文小组的人数是甲班没有参加人数的 。甲班没有参加的人数是乙班没有参加人数的几分之几?
2532380249555
我当小老师
本堂课所学的知识有哪些?(口述) 你最喜欢的方法是什么,列举一道题说明,最难的题型是什么?
课后作业
一桶油20千克,用去一些后还剩下 。用去多少千克?
师徒两人共同加工一批零件,3天完成了 ,已知师傅独做需要20天完成。徒弟独做需要多少天完成?
3087370-75565一辆汽车从甲地去乙地,已行了全程的 ,这时距中点还有15千米。已行了多少千米?
邮递员往山区送报,去时每小时走 千米,走了 小时到达;到达后立即返回,这样往返一共用了1 小时。求邮递员返回时平均每小时走多少千米?
三家合用一捆电线,甲家用了全长的 ,正好是45米,乙、丙两家按7:8正好用完,乙、丙两家各用多少米?
有甲、乙两块长方形试验田,甲长40米,宽30米,乙长50米,宽60米,现把350千克化肥按面积进行分配,甲、乙试验田各应分到多少千克?
2532380224155
1、将本堂课错题本中的练习再做一遍。
2、你平时还遇到什么分数应用题是今天老师还没讲到的,请写在下面,下次课我们一起解决。
2532380217805
课首小测
1.(1) ; ; ;①30× ;②30× ;③30×
(2) 1 ; ; ; 1 );①60÷ ;②60÷ × ;③60÷ ×1
49377603790955307965379095(3)1 ; 1 ; ; 2 ;①60×1 ; ②60× ;③60×2 ;
(4)1 ; ; ; 1 ;①60÷ ; ②60÷ × ;③60÷ ×1
2421255-311152.(1)50× ;(2)30÷(1- )× ;(3)100×(1+ );
1699895-311154660265-31115(4)280+280÷(1- ) ;(5)30÷(1- );(6)125-125÷(1+ )
3.①25÷20; ②20÷25;③(25-20)÷20 ;
④(25-20)÷25; ⑤25÷(25+20); ⑥20÷(25+20)
4.2790米
5.826米
6.48张
导学一
知识点讲解 1 例题
7010402152651.820米
解析:
导学二
知识点讲解 1 例题
10896601784351.苹果树:240棵#梨树:180棵
解析:梨树: (棵)
苹果树:420-180=240(棵)
导学三
知识点讲解 1 例题
1.150千克
导学四
知识点讲解 1 例题
1.24人
导学五
知识点讲解 1 例题
1.甲:240元;乙:160元
我爱展示
1.244页
2.甲:30;乙:16
3.12人
4.600个
4972052413005.500棵
6.
课后作业
1.12千克
2.30天
3.60千米
4.10千米
5.乙63米;丙72米
6.甲:100千克#乙:250千克
同课章节目录
