2.2 函数的概念习题课 课件(41张PPT)
文档属性
| 名称 | 2.2 函数的概念习题课 课件(41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 394.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 09:14:59 | ||
图片预览











文档简介
函数的概念及其表示习题课
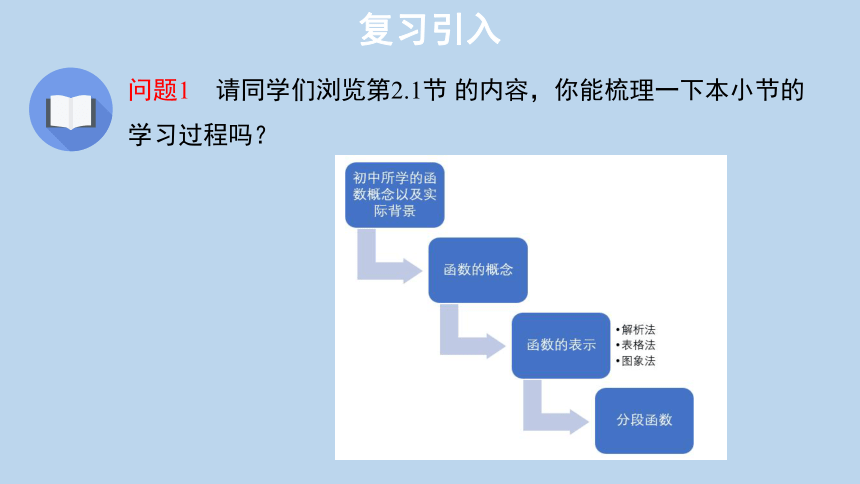
问题1 请同学们浏览第2.1节 的内容,你能梳理一下本小节的学习过程吗?
复习引入
1.函数的概念及其构成要素
新知探究
新知探究
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
追问 求解函数定义域的一般步骤是什么?
第一步:根据解析式有意义转化成不等式;
第二步:解不等式或不等式组求得原来函数的定义域.
新知探究
解:(1)要使该函数有意义,则需x-4≠0.
解得:x≠4.
所以函数f(x)的定义域为(-∞,4)∪(4,+∞).
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
新知探究
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
解:(2)要使该函数有意义,则需x2≥0.
解得:x∈R.
所以函数f(x)的定义域为R.
新知探究
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
解:(3)要使该函数有意义,则需x2-3x+2≠0.
解得:x≠1且x≠2.
所以函数f(x)的定义域为 {x|x≠1且x≠2}.
所以函数f(x)的定义域为(-∞,1)∪(1,4].
解:(4)要使该函数有意义,则需
解得:
新知探究
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
例2 下列哪一组中的函数f(x)与g(x)是同一个函数?
(1)f(x)=x-1,g(x)= -1;
(2)f(x)=x2,g(x)=( )4;
(3)f(x)=x2,g(x)= .
新知探究
追问 判断两个函数是否相等的一般的步骤是什么?
第一步,求两个函数的定义域.
第二步,判断定义域是否相同.
若否,则不是相等函数,结束判断;
若是,则进行第三步.
第三步,化简两个函数的解析式,若解析式也相同,则为相等函数;若解析式不相同,则不是相等函数.
新知探究
(1)f(x)=x-1,g(x)= -1;
解:第(1)组中,f(x)=x-1的定义域为R,
所以不是同一个函数.
g(x)= -1的定义域为{x|x≠0},定义域不同,
新知探究
例2 下列哪一组中的函数f(x)与g(x)是同一个函数?
(2)f(x)=x2,g(x)=( )4;
解:第(2)组中,f(x)=x2的定义域为R,
所以不是同一个函数.
g(x)=( )4的定义域为{x|x≥0},定义域不同,
新知探究
例2 下列哪一组中的函数f(x)与g(x)是同一个函数?
(3)f(x)=x2,g(x)= .
解:第(3)组中,二者的定义域均为R,
所以f(x)=x2与g(x)= 是同一个函数.
新知探究
且 =x2,因此解析式也相同,
例2 下列哪一组中的函数f(x)与g(x)是同一个函数?
(1)任给u∈A,对应关系f使方程①的解v与u对应,判断v=f(u)是否为函数并说明理由;
(2)任给v∈B,对应关系g使方程①的解v与u对应,判断u=g(v)是否为函数并说明理由.
新知探究
例3 给定数集A=R,B=(-∞,0],方程
u2+2v=0, ①
追问1 判断某个给定的对应关系是否函数的依据是什么?
判断的依据是函数的概念.
具体内容是:
对于数集A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数.
新知探究
例3 给定数集A=R,B=(-∞,0],方程
u2+2v=0, ①
(1)任给u∈A,对应关系f使方程①的解v与u对应,判断v=f(u)是否为函数并说明理由;
解:(1)根据u2+2v=0,可得v=- ,
任给u∈A,根据对应关系v=- ,
在数集B中都能找到唯一的元素v=- 与之对应,所以是函数.
新知探究
(2)任给v∈B,对应关系g使方程①的解v与u对应,判断u=g(v)是否为函数并说明理由.
解:(2)根据u2+2v=0,可得u=± ,
任给v∈B且v≠0,根据对应关系u=± ,
在数集A中都能找到两个元素u=± 与之对应,所以不是函数.
新知探究
例3 给定数集A=R,B=(-∞,0],方程
u2+2v=0, ①
追问2 结合v=f(u)和u=g(v)的图象验证你的判断,其中v=f(u)和u=g(v)的图象分别如图1和图2.
图1
o
u
v
图2
o
u
v
根据图1,在横轴上任取一点u=u0,
过该点作横轴的垂线,与曲线有且
仅有一个交点(u0,v0)(如图),
即对于任意的u0∈R,
u0
u0 ,v0
新知探究
所以v=f(u)是函数.
按照对应关系①有唯一的v0与之对应,
图2
o
u
v
图1
o
u
v
追问2 结合v=f(u)和u=g(v)的图象验证你的判断,其中v=f(u)和u=g(v)的图象分别如图1和图2.
新知探究
v0 ,v0
v0 ,-u0
v0
根据图2,在横轴负半轴上任取一点v=v0,
过该点作横轴的垂线,与曲线有两个交点
(v0,u0)、(v0,-u0)(如图),
即对于任意的v0∈(-∞,0),
所以u=g(v)不是函数.
按照对应关系①有两个值与之对应,
u0
u0 ,v0
追问3 根据方程u2+2v=0,写出一个对应关系h使它成为u关于v的函数.
u=- 或u= .
新知探究
2.求函数的解析式
新知探究
例4 (1)已知f(x)是二次函数,且满足f(0)=1,
f(x+1)-f(x)=2x,求f(x)的解析式;
(2)已知f(x+1)=x2-3x+2,求f(x);
(3)已知函数f(x)对于任意的x都有
f(x)+2f(-x)=3x-2,求f(x).
新知探究
解:(1)由f(x)是二次函数,设f(x)=ax2+bx+c(a≠0),
由f(0)=1,得c=1,
则f(x+1)-f(x)=a(x+1)2+b(x+1)+1-(ax2+bx+1)
=2ax+a+b=2x
这个式子对于任意x∈R均成立,
所以2a=2,a+b=0,可得a=1,b=-1,
解析式为f(x)=x2-x+1.
新知探究
例4 (1)已知f(x)是二次函数,且满足f(0)=1,
f(x+1)-f(x)=2x,求f(x)的解析式;
例4 (2)已知f(x+1)=x2-3x+2,求f(x);
将x=t-1代入f(x+1)=x2-3x+2,
得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
则解析式为f(x)=x2-5x+6.
解:(2)方法一:令x+1=t,则x=t-1.
新知探究
例4 (2)已知f(x+1)=x2-3x+2,求f(x);
解:(2)方法二:
新知探究
x2-3x+2=(x+1)2-2x-1-3x+2=(x+1)2-5x+1
=(x+1)2-5(x+1)+5+1=(x+1)2-5(x+1)+6,
即f(x+1)=(x+1)2-5(x+1)+6,
则解析式为f(x)=x2-5x+6.
解:(3)因为对于任意的x都有f(x)+2f(-x)=3x-2 ……②,
所以f(-x)+2f(-(-x))=3×(-x)-2,
即2f(x)+f(-x)=-3x-2 ……③,
2×③-②得:3f(x)=-9x-2,
则解析式为f(x)=-3x- .
新知探究
例4 (3)已知函数f(x)对于任意的x都有
f(x)+2f(-x)=3x-2,求f(x).
第(1)题中的方法叫待定系数法.
适用于当函数类型给定,且函数某些性质已知时求函数解析式的题型.
第(2)题中的方法一叫换元法.
适用于已知函数f(g(x))的表达式,求f(x)的解析式的题型.
具体做法是:
令g(x)=t,并反解出x,
然后x把代入f(g(x))的表达式中,求出f(t),从而求出f(x);
新知探究
总结提升:
第(2)题中的方法二叫凑配法.
适用于已知函数f(g(x))的解析式,且f(g(x))的表达式可变形为关于g(x)的形式.
具体做法是:
将式子两端的g(x)看成一个整体代换为函数的自变量,从而求出f(x);
在这两种方法中,都要注意函数的定义域,方法一中函数的定义域为新元t的取值范围;方法二中函数的定义域为g(x)的值域.
新知探究
总结提升:
第(3)题中的方法叫方程组法.
具体做法是:
适用于当函数f(x)满足形如af(x)+bf(-x)=g(x)(a≠b且ab≠0)或af(x)+bf( )=g(x)(a≠b且ab≠0)等关系时.
我们可以用-x或 代替关系式中的x,将得到的新式子与原关系式联立方程组,经消元后将f(x)从方程组中解出来.
新知探究
总结提升:
3.分段函数
新知探究
例5 函数f(x)=[x]的函数值,表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2.当x∈(-2.5,3]时,写出函数f(x)的解析式,并画出函数f(x)的图象.
新知探究
解:
函数f(x)的图象如图.
追问1 设函数g(x)=x-[x],x∈(-2.5,3],写出函数g(x)的解析式,并画出函数g(x)的图象.
函数g(x)的图象如图.
解:
新知探究
追问2 求函数f(x)与g(x)的值域.
函数f(x)的值域为{-3,-2,-1,0,1,2,3},
函数g(x)的值域为[0,1).
新知探究
追问3 求方程g(x)=0.5的解集.
当-2.5<x<-2时,令g(x)=0.5,则x+3=0.5,
解得x=-2.5,-2.5?(-2.5,-2),此时方程无解;
当-2<x<-1时,令g(x)=0.5,则x+2=0.5,
解得x=-1.5,-1.5∈[-2,-1),此时方程的解为x=-1.5;
同理可以求得其他区间内的解.
综上,方程g(x)=0.5的解集为{-1.5,-0.5,0.5,1.5,2.5}.
新知探究
(1)对应关系f是函数的核心要素,只要满足:对于数集A中的任意一个数x,按照对应关系f,在集合B中都有唯一确定的数y和它对应,那么f:A→B就为从集合A到集合B的一个函数;
它的表现形式多种多样:文字语言、解析式、表格、图象、方程等,可以根据需要灵活选择.
归纳小结
问题2 回忆本节课的内容,请你回答以下几个问题:
(1)你能谈谈对函数的对应关系的认识吗?
(2)你能谈谈函数图象在解决问题中的作用吗?
问题2 回忆本节课的内容,请你回答以下几个问题:
(1)你能谈谈对函数的对应关系的认识吗?
(2)你能谈谈函数图象在解决问题中的作用吗?
(2)函数图象很直观,在解题过程中常用来帮助理解问题的数学本质,依托函数图象可以更直观地寻求问题的解决思路和要点.
归纳小结
1.下列四组函数中,表示同一函数的一组是( )
2.函数y= 定义域是______________________.
目标检测
A.y=|x|,u= B.y= ,s=( )2
C.y= ,m=n+1 D.y= ,y=
3.f(x)= 若f(x)=10,则x=___________.
A
[-1,2)∪(2,+∞)
-3
1
2
3
4.某位同学要在暑假的八月上旬完成一定量的英语单词的记忆,计划是:第一天记忆300个单词;第一天后的每一天,在复习前面记忆的单词的基础上增加50个新单词的记忆量.
该同学记忆的单词总量y是关于记忆天数x的函数吗?如果是,你能用哪些方法表示这个函数;如果不是,请你说明理由.
目标检测
解:用x表示记忆天数,用y表示记忆的单词总量,
那么y=50x+250,x∈A,
其中A={1,2,3,4,5,6,7,8,9,10}.
该同学记忆的单词总量y是关于记忆天数x的函数.
4
原因如下:
4.某位同学要在暑假的八月上旬完成一定量的英语单词的记忆,计划是:第一天记忆300个单词;第一天后的每一天,在复习前面记忆的单词的基础上增加50个新单词的记忆量.
该同学记忆的单词总量y是关于记忆天数x的函数吗?如果是,你能用哪些方法表示这个函数;如果不是,请你说明理由.
目标检测
解:对于数集A={1,2,3,4,5,6,7,8,9,10}中的任一个天数x,
根据对应关系y=50x+250,
在数集B={300,350,400,450,500,550,600,650,700,750}中,
4
都有唯一的单词总量y与之对应.
目标检测
用解析法可将该函数表示为
y=50x+250,x∈{1,2,3,4,5,6,7,8,9,10}.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}记忆天数x
1
2
3
4
5
6
7
8
9
10
记忆的单词总量y
300
350
400
450
500
550
600
650
700
750
用图象法可将该函数表示为右图.
用列表法可将该函数表示为
再见
问题1 请同学们浏览第2.1节 的内容,你能梳理一下本小节的学习过程吗?
复习引入
1.函数的概念及其构成要素
新知探究
新知探究
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
追问 求解函数定义域的一般步骤是什么?
第一步:根据解析式有意义转化成不等式;
第二步:解不等式或不等式组求得原来函数的定义域.
新知探究
解:(1)要使该函数有意义,则需x-4≠0.
解得:x≠4.
所以函数f(x)的定义域为(-∞,4)∪(4,+∞).
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
新知探究
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
解:(2)要使该函数有意义,则需x2≥0.
解得:x∈R.
所以函数f(x)的定义域为R.
新知探究
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
解:(3)要使该函数有意义,则需x2-3x+2≠0.
解得:x≠1且x≠2.
所以函数f(x)的定义域为 {x|x≠1且x≠2}.
所以函数f(x)的定义域为(-∞,1)∪(1,4].
解:(4)要使该函数有意义,则需
解得:
新知探究
例1 求下列函数的定义域:
(1)f(x)= ;
(2)f(x)= ;
(3)f(x)= ;
(4)f(x)= .
例2 下列哪一组中的函数f(x)与g(x)是同一个函数?
(1)f(x)=x-1,g(x)= -1;
(2)f(x)=x2,g(x)=( )4;
(3)f(x)=x2,g(x)= .
新知探究
追问 判断两个函数是否相等的一般的步骤是什么?
第一步,求两个函数的定义域.
第二步,判断定义域是否相同.
若否,则不是相等函数,结束判断;
若是,则进行第三步.
第三步,化简两个函数的解析式,若解析式也相同,则为相等函数;若解析式不相同,则不是相等函数.
新知探究
(1)f(x)=x-1,g(x)= -1;
解:第(1)组中,f(x)=x-1的定义域为R,
所以不是同一个函数.
g(x)= -1的定义域为{x|x≠0},定义域不同,
新知探究
例2 下列哪一组中的函数f(x)与g(x)是同一个函数?
(2)f(x)=x2,g(x)=( )4;
解:第(2)组中,f(x)=x2的定义域为R,
所以不是同一个函数.
g(x)=( )4的定义域为{x|x≥0},定义域不同,
新知探究
例2 下列哪一组中的函数f(x)与g(x)是同一个函数?
(3)f(x)=x2,g(x)= .
解:第(3)组中,二者的定义域均为R,
所以f(x)=x2与g(x)= 是同一个函数.
新知探究
且 =x2,因此解析式也相同,
例2 下列哪一组中的函数f(x)与g(x)是同一个函数?
(1)任给u∈A,对应关系f使方程①的解v与u对应,判断v=f(u)是否为函数并说明理由;
(2)任给v∈B,对应关系g使方程①的解v与u对应,判断u=g(v)是否为函数并说明理由.
新知探究
例3 给定数集A=R,B=(-∞,0],方程
u2+2v=0, ①
追问1 判断某个给定的对应关系是否函数的依据是什么?
判断的依据是函数的概念.
具体内容是:
对于数集A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数.
新知探究
例3 给定数集A=R,B=(-∞,0],方程
u2+2v=0, ①
(1)任给u∈A,对应关系f使方程①的解v与u对应,判断v=f(u)是否为函数并说明理由;
解:(1)根据u2+2v=0,可得v=- ,
任给u∈A,根据对应关系v=- ,
在数集B中都能找到唯一的元素v=- 与之对应,所以是函数.
新知探究
(2)任给v∈B,对应关系g使方程①的解v与u对应,判断u=g(v)是否为函数并说明理由.
解:(2)根据u2+2v=0,可得u=± ,
任给v∈B且v≠0,根据对应关系u=± ,
在数集A中都能找到两个元素u=± 与之对应,所以不是函数.
新知探究
例3 给定数集A=R,B=(-∞,0],方程
u2+2v=0, ①
追问2 结合v=f(u)和u=g(v)的图象验证你的判断,其中v=f(u)和u=g(v)的图象分别如图1和图2.
图1
o
u
v
图2
o
u
v
根据图1,在横轴上任取一点u=u0,
过该点作横轴的垂线,与曲线有且
仅有一个交点(u0,v0)(如图),
即对于任意的u0∈R,
u0
u0 ,v0
新知探究
所以v=f(u)是函数.
按照对应关系①有唯一的v0与之对应,
图2
o
u
v
图1
o
u
v
追问2 结合v=f(u)和u=g(v)的图象验证你的判断,其中v=f(u)和u=g(v)的图象分别如图1和图2.
新知探究
v0 ,v0
v0 ,-u0
v0
根据图2,在横轴负半轴上任取一点v=v0,
过该点作横轴的垂线,与曲线有两个交点
(v0,u0)、(v0,-u0)(如图),
即对于任意的v0∈(-∞,0),
所以u=g(v)不是函数.
按照对应关系①有两个值与之对应,
u0
u0 ,v0
追问3 根据方程u2+2v=0,写出一个对应关系h使它成为u关于v的函数.
u=- 或u= .
新知探究
2.求函数的解析式
新知探究
例4 (1)已知f(x)是二次函数,且满足f(0)=1,
f(x+1)-f(x)=2x,求f(x)的解析式;
(2)已知f(x+1)=x2-3x+2,求f(x);
(3)已知函数f(x)对于任意的x都有
f(x)+2f(-x)=3x-2,求f(x).
新知探究
解:(1)由f(x)是二次函数,设f(x)=ax2+bx+c(a≠0),
由f(0)=1,得c=1,
则f(x+1)-f(x)=a(x+1)2+b(x+1)+1-(ax2+bx+1)
=2ax+a+b=2x
这个式子对于任意x∈R均成立,
所以2a=2,a+b=0,可得a=1,b=-1,
解析式为f(x)=x2-x+1.
新知探究
例4 (1)已知f(x)是二次函数,且满足f(0)=1,
f(x+1)-f(x)=2x,求f(x)的解析式;
例4 (2)已知f(x+1)=x2-3x+2,求f(x);
将x=t-1代入f(x+1)=x2-3x+2,
得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
则解析式为f(x)=x2-5x+6.
解:(2)方法一:令x+1=t,则x=t-1.
新知探究
例4 (2)已知f(x+1)=x2-3x+2,求f(x);
解:(2)方法二:
新知探究
x2-3x+2=(x+1)2-2x-1-3x+2=(x+1)2-5x+1
=(x+1)2-5(x+1)+5+1=(x+1)2-5(x+1)+6,
即f(x+1)=(x+1)2-5(x+1)+6,
则解析式为f(x)=x2-5x+6.
解:(3)因为对于任意的x都有f(x)+2f(-x)=3x-2 ……②,
所以f(-x)+2f(-(-x))=3×(-x)-2,
即2f(x)+f(-x)=-3x-2 ……③,
2×③-②得:3f(x)=-9x-2,
则解析式为f(x)=-3x- .
新知探究
例4 (3)已知函数f(x)对于任意的x都有
f(x)+2f(-x)=3x-2,求f(x).
第(1)题中的方法叫待定系数法.
适用于当函数类型给定,且函数某些性质已知时求函数解析式的题型.
第(2)题中的方法一叫换元法.
适用于已知函数f(g(x))的表达式,求f(x)的解析式的题型.
具体做法是:
令g(x)=t,并反解出x,
然后x把代入f(g(x))的表达式中,求出f(t),从而求出f(x);
新知探究
总结提升:
第(2)题中的方法二叫凑配法.
适用于已知函数f(g(x))的解析式,且f(g(x))的表达式可变形为关于g(x)的形式.
具体做法是:
将式子两端的g(x)看成一个整体代换为函数的自变量,从而求出f(x);
在这两种方法中,都要注意函数的定义域,方法一中函数的定义域为新元t的取值范围;方法二中函数的定义域为g(x)的值域.
新知探究
总结提升:
第(3)题中的方法叫方程组法.
具体做法是:
适用于当函数f(x)满足形如af(x)+bf(-x)=g(x)(a≠b且ab≠0)或af(x)+bf( )=g(x)(a≠b且ab≠0)等关系时.
我们可以用-x或 代替关系式中的x,将得到的新式子与原关系式联立方程组,经消元后将f(x)从方程组中解出来.
新知探究
总结提升:
3.分段函数
新知探究
例5 函数f(x)=[x]的函数值,表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2.当x∈(-2.5,3]时,写出函数f(x)的解析式,并画出函数f(x)的图象.
新知探究
解:
函数f(x)的图象如图.
追问1 设函数g(x)=x-[x],x∈(-2.5,3],写出函数g(x)的解析式,并画出函数g(x)的图象.
函数g(x)的图象如图.
解:
新知探究
追问2 求函数f(x)与g(x)的值域.
函数f(x)的值域为{-3,-2,-1,0,1,2,3},
函数g(x)的值域为[0,1).
新知探究
追问3 求方程g(x)=0.5的解集.
当-2.5<x<-2时,令g(x)=0.5,则x+3=0.5,
解得x=-2.5,-2.5?(-2.5,-2),此时方程无解;
当-2<x<-1时,令g(x)=0.5,则x+2=0.5,
解得x=-1.5,-1.5∈[-2,-1),此时方程的解为x=-1.5;
同理可以求得其他区间内的解.
综上,方程g(x)=0.5的解集为{-1.5,-0.5,0.5,1.5,2.5}.
新知探究
(1)对应关系f是函数的核心要素,只要满足:对于数集A中的任意一个数x,按照对应关系f,在集合B中都有唯一确定的数y和它对应,那么f:A→B就为从集合A到集合B的一个函数;
它的表现形式多种多样:文字语言、解析式、表格、图象、方程等,可以根据需要灵活选择.
归纳小结
问题2 回忆本节课的内容,请你回答以下几个问题:
(1)你能谈谈对函数的对应关系的认识吗?
(2)你能谈谈函数图象在解决问题中的作用吗?
问题2 回忆本节课的内容,请你回答以下几个问题:
(1)你能谈谈对函数的对应关系的认识吗?
(2)你能谈谈函数图象在解决问题中的作用吗?
(2)函数图象很直观,在解题过程中常用来帮助理解问题的数学本质,依托函数图象可以更直观地寻求问题的解决思路和要点.
归纳小结
1.下列四组函数中,表示同一函数的一组是( )
2.函数y= 定义域是______________________.
目标检测
A.y=|x|,u= B.y= ,s=( )2
C.y= ,m=n+1 D.y= ,y=
3.f(x)= 若f(x)=10,则x=___________.
A
[-1,2)∪(2,+∞)
-3
1
2
3
4.某位同学要在暑假的八月上旬完成一定量的英语单词的记忆,计划是:第一天记忆300个单词;第一天后的每一天,在复习前面记忆的单词的基础上增加50个新单词的记忆量.
该同学记忆的单词总量y是关于记忆天数x的函数吗?如果是,你能用哪些方法表示这个函数;如果不是,请你说明理由.
目标检测
解:用x表示记忆天数,用y表示记忆的单词总量,
那么y=50x+250,x∈A,
其中A={1,2,3,4,5,6,7,8,9,10}.
该同学记忆的单词总量y是关于记忆天数x的函数.
4
原因如下:
4.某位同学要在暑假的八月上旬完成一定量的英语单词的记忆,计划是:第一天记忆300个单词;第一天后的每一天,在复习前面记忆的单词的基础上增加50个新单词的记忆量.
该同学记忆的单词总量y是关于记忆天数x的函数吗?如果是,你能用哪些方法表示这个函数;如果不是,请你说明理由.
目标检测
解:对于数集A={1,2,3,4,5,6,7,8,9,10}中的任一个天数x,
根据对应关系y=50x+250,
在数集B={300,350,400,450,500,550,600,650,700,750}中,
4
都有唯一的单词总量y与之对应.
目标检测
用解析法可将该函数表示为
y=50x+250,x∈{1,2,3,4,5,6,7,8,9,10}.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}记忆天数x
1
2
3
4
5
6
7
8
9
10
记忆的单词总量y
300
350
400
450
500
550
600
650
700
750
用图象法可将该函数表示为右图.
用列表法可将该函数表示为
再见
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
