13.2 整式的乘法(第2课时 单项式与多项式相乘)
文档属性
| 名称 | 13.2 整式的乘法(第2课时 单项式与多项式相乘) |

|
|
| 格式 | rar | ||
| 文件大小 | 823.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-14 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
华东师大版八年级(上册)
第13章 整式的乘除
13.2 整式的乘法(第2课时)
单项式与单项式相乘
相同字母的幂相乘
只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式
系数乘以系数
复习巩固
计算:
解:
=
=
相同字母的指数的和作为积里这个字母的指数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
各因式系数的积作为积的系数
1.-4mn3·3mn2
2.-3a2c·(-2ab2)2
3.3x·(-4x2y)·2y
4.光速约为3×108米/秒,太阳光射到地球上的时间约为5×102秒,则地球与太阳的距离约为多少米?
2
3
4
5
1
12
11
10
9
8
7
6
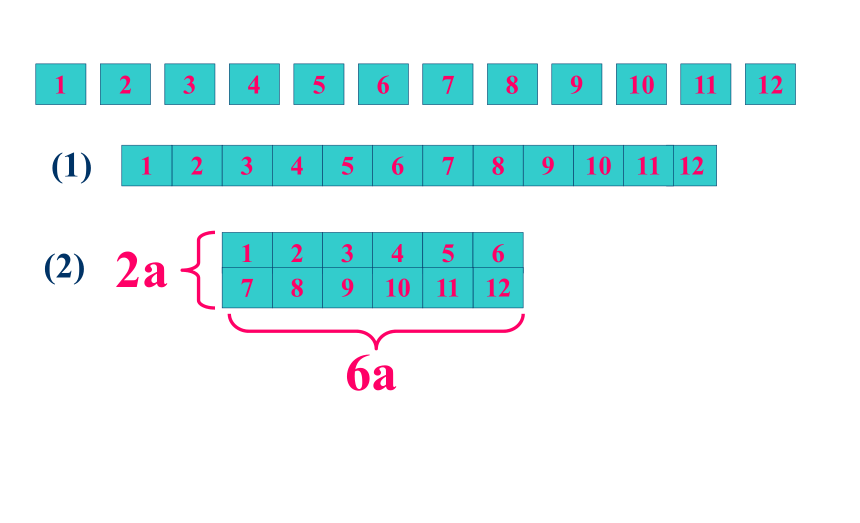
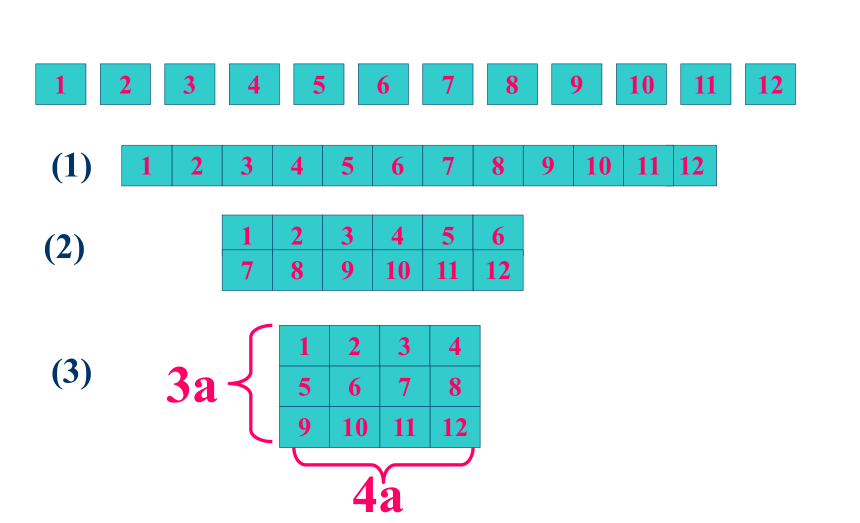
用12块边长为a的正方形纸片拼成一个长方形。有几种不同的拼法?请你找出来。
探究性作业
2
3
4
5
1
12
11
10
9
8
7
6
2
3
4
5
1
12
11
10
9
8
7
6
(1)
12a
a
2
3
4
5
1
12
11
10
9
8
7
6
2
3
4
5
1
6
12
11
10
9
8
7
2
3
4
5
1
12
11
10
9
8
7
6
(1)
(2)
2a
6a
2
3
4
5
1
12
11
10
9
8
7
6
2
3
4
5
1
6
12
11
10
9
8
7
2
3
1
4
5
8
7
6
12
11
10
9
2
3
4
5
1
12
11
10
9
8
7
6
(1)
(2)
(3)
4a
3a
同底数幂相乘:底数 ,指数 .
am · an = (m,n都是正整数)
4am -am = .
合并同类项:系数 , 与 的 不变.
(am)n= (m,n都是正整数).
幂的乘方:底数 ,指数 .
(ab)n = (m,n都是正整数)
积的乘方:各因式分别 后的 .即 的 .
单项式与单项式相乘,只要将它们的 、 的幂分别相乘,对于只在单项式中出现的字母,则连同它的指数 一起作为积的一个因式。
几个单项式的代数和叫做多项式. 如:2x2-x-1,它的项是:2x2,-x,-1.
什么叫多项式
复习巩固
你记得乘法分配律吗 x(a+b) =
1
2
x · (a + b)
=
xa
1
2
+xb
法则:单项式与多项式相乘,只要将单项式分别乘以多项式的每一项,再将所得的积相加。
公式:
讲授新知
解 : 3a2 (3a-2b3)
=3a2 3a + 3a2 (-2b3)
=9a3- 6a2b3
例1 计算3a2 (3a-2b3)
课堂训练
解: (-3a2) (2ab2-4ab3)
=(-3a2) 2ab2+(-3a2) (-4ab3)
=-6a3b2+12a3b3
例2 计算(-3a2) (2ab2-4ab3)
解:原式= - a3b - 2a2b 2 - 5a3b+5a2b2
= - 6a3b+3a2b2
当a=-1,b=2时
例3 化简求值:
-2a2 ( ab+b2)- 5a(a2b - ab2),其中a=-1,b=2
求值问题,方法不是唯一的,可以直接把字母的值代入原式,但计算烦琐易出错,应先化简,再代入求值,就显得非常简捷。
课堂练习
例4 如图,计算左面图形的体积(黄、红长方体的各项尺寸相等).
3x
3x
2x
2x
2x+5
1. 计算:
(1)3x3y (2xy2-3xy);
(2)2x (3x2-xy+y2).
2. 化简:
x(x2-1)+2x2(x+1)-3x(2x-5).
课堂小测
课堂练习
小结:
1、单项式与多项式相乘的依据是:乘法对加法的分配律。
2、单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数 相同,注意不要漏乘项。
4. 求值问题,方法不是唯一的,可以直接把字母的值代入原式,但计算烦琐易出错,应
先化简,再代入求值,就显得非常简捷。
3、积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意去括号法则。
华东师大版八年级(上册)
第13章 整式的乘除
13.2 整式的乘法(第2课时)
单项式与单项式相乘
相同字母的幂相乘
只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式
系数乘以系数
复习巩固
计算:
解:
=
=
相同字母的指数的和作为积里这个字母的指数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
各因式系数的积作为积的系数
1.-4mn3·3mn2
2.-3a2c·(-2ab2)2
3.3x·(-4x2y)·2y
4.光速约为3×108米/秒,太阳光射到地球上的时间约为5×102秒,则地球与太阳的距离约为多少米?
2
3
4
5
1
12
11
10
9
8
7
6
用12块边长为a的正方形纸片拼成一个长方形。有几种不同的拼法?请你找出来。
探究性作业
2
3
4
5
1
12
11
10
9
8
7
6
2
3
4
5
1
12
11
10
9
8
7
6
(1)
12a
a
2
3
4
5
1
12
11
10
9
8
7
6
2
3
4
5
1
6
12
11
10
9
8
7
2
3
4
5
1
12
11
10
9
8
7
6
(1)
(2)
2a
6a
2
3
4
5
1
12
11
10
9
8
7
6
2
3
4
5
1
6
12
11
10
9
8
7
2
3
1
4
5
8
7
6
12
11
10
9
2
3
4
5
1
12
11
10
9
8
7
6
(1)
(2)
(3)
4a
3a
同底数幂相乘:底数 ,指数 .
am · an = (m,n都是正整数)
4am -am = .
合并同类项:系数 , 与 的 不变.
(am)n= (m,n都是正整数).
幂的乘方:底数 ,指数 .
(ab)n = (m,n都是正整数)
积的乘方:各因式分别 后的 .即 的 .
单项式与单项式相乘,只要将它们的 、 的幂分别相乘,对于只在单项式中出现的字母,则连同它的指数 一起作为积的一个因式。
几个单项式的代数和叫做多项式. 如:2x2-x-1,它的项是:2x2,-x,-1.
什么叫多项式
复习巩固
你记得乘法分配律吗 x(a+b) =
1
2
x · (a + b)
=
xa
1
2
+xb
法则:单项式与多项式相乘,只要将单项式分别乘以多项式的每一项,再将所得的积相加。
公式:
讲授新知
解 : 3a2 (3a-2b3)
=3a2 3a + 3a2 (-2b3)
=9a3- 6a2b3
例1 计算3a2 (3a-2b3)
课堂训练
解: (-3a2) (2ab2-4ab3)
=(-3a2) 2ab2+(-3a2) (-4ab3)
=-6a3b2+12a3b3
例2 计算(-3a2) (2ab2-4ab3)
解:原式= - a3b - 2a2b 2 - 5a3b+5a2b2
= - 6a3b+3a2b2
当a=-1,b=2时
例3 化简求值:
-2a2 ( ab+b2)- 5a(a2b - ab2),其中a=-1,b=2
求值问题,方法不是唯一的,可以直接把字母的值代入原式,但计算烦琐易出错,应先化简,再代入求值,就显得非常简捷。
课堂练习
例4 如图,计算左面图形的体积(黄、红长方体的各项尺寸相等).
3x
3x
2x
2x
2x+5
1. 计算:
(1)3x3y (2xy2-3xy);
(2)2x (3x2-xy+y2).
2. 化简:
x(x2-1)+2x2(x+1)-3x(2x-5).
课堂小测
课堂练习
小结:
1、单项式与多项式相乘的依据是:乘法对加法的分配律。
2、单项式与多项式相乘,其积仍是多项式,项数与原多项式的项数 相同,注意不要漏乘项。
4. 求值问题,方法不是唯一的,可以直接把字母的值代入原式,但计算烦琐易出错,应
先化简,再代入求值,就显得非常简捷。
3、积的每一项的符号由原多项式各项符号和单项式的符号来决定,注意去括号法则。
