2.4函数的基本性质习题课 课件(28张ppt)
文档属性
| 名称 | 2.4函数的基本性质习题课 课件(28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 279.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览








文档简介
函数的基本性质习题课
问题1 请同学们梳理第3.2节(课本P76~P85)的内容,回答以下几个问题:
复习引入
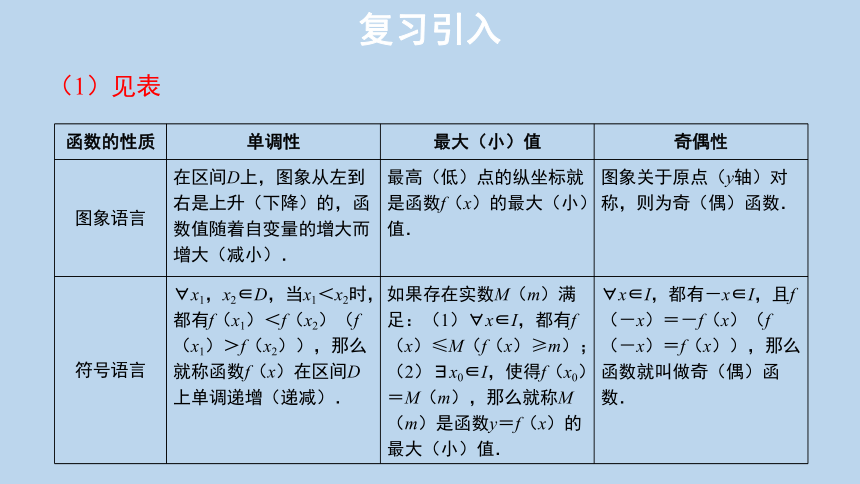
(1)函数的基本性质有哪些?你能依次从图象特征和代数符号的角度叙述这些性质吗?
(2)你能说说研究函数的性质的方法吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数的性质
单调性
最大(小)值
奇偶性
图象语言
在区间D上,图象从左到右是上升(下降)的,函数值随着自变量的增大而增大(减小).
最高(低)点的纵坐标就是函数f(x)的最大(小)值.
图象关于原点(y轴)对称,则为奇(偶)函数.
符号语言
?x1,x2∈D,当x1<x2时,都有f(x1)<f(x2)(f(x1)>f(x2)),那么就称函数f(x)在区间D上单调递增(递减).
如果存在实数M(m)满足:(1)?x∈I,都有f(x)≤M(f(x)≥m);(2)?x0∈I,使得f(x0)=M(m),那么就称M(m)是函数y=f(x)的最大(小)值.
?x∈I,都有-x∈I,且f(-x)=-f(x)(f(-x)=f(x)),那么函数就叫做奇(偶)函数.
(1)见表
复习引入
复习引入
(2)你能说说研究函数的性质的方法吗?
先观察具体函数图象,分析图象特征,
再结合解析式从代数的角度定量刻画函数性质,抽象出一般概念;
最后应用概念分析解决问题.
形成对函数性质的感性认识;
问题1 请同学们梳理第3.2节(课本P76~P85)的内容,回答以下几个问题:
1.单调性的应用
新知探究
新知探究
(1)根据函数单调性的定义证明函数y=x+ 在区间(3,+∞)上单调递增;
(2)讨论函数y=x+ 在区间(0,+∞)上的单调性;
(3)讨论函数y=x+ (k>0)在区间(0,+∞)上的单调性.
例1(习题3.2 P86第8题)
新知探究
证明:?x1,x2∈(3,+∞),且x1<x2,
有y1-y2=(x1+ )-(x2+ )
=(x1-x2)+( - )
=(x1-x2)+
=(x1-x2)-(1- )
=(x1-x2)( )
例1(习题3.2 P86第8题)
(1)根据函数单调性的定义证明函数y=x+ 在区间(3,+∞)上单调递增;
新知探究
证明:由x1,x2∈(3,+∞),得x1>3,x2>3,
所以x1x2>9,x1x2-9>0.
由x1<x2,得x1-x2<0,
于是(x1-x2)( )<0,即y1<y2.
所以,函数y=x+ 在区间(3,+∞)上的单调递增.
(1)根据函数单调性的定义证明函数y=x+ 在区间(3,+∞)上单调递增;
例1(习题3.2 P86第8题)
新知探究
(2)讨论函数y=x+ 在区间(0,+∞)上的单调性;
解:当x1,x2∈(0,3)时,x1x2-9<0,
在区间(3,+∞)上单调递增.
则y1-y2>0,即y1>y2,
所以y=x+ 在区间(0,3)上单调递减.
综上,y=x+ 在区间(0,3)上单调递减,
例1(习题3.2 P86第8题)
新知探究
(3)讨论函数y=x+ (k>0)在区间(0,+∞)上的单调性.
解:函数y=x+ (k>0)在区间(0, ]上单调递减,
在区间[ ,+∞)上单调递增.
例1(习题3.2 P86第8题)
追问1 判断函数y=x+ (k>0)在区间(0,+∞)上是否存在最值并说明理由;
根据函数y=x+ (k>0)的单调性,
可知该函数在x= 处取到最小值,最小值为2 ,无最大值.
新知探究
追问2 函数y=x+ (k>0)在区间[2,3]上具有单调性,求k的取值范围;
解得:k≥9或0<k≤4,
由该函数的单调性可知:3≤ 或2≥ ,
所以k的取值范围为(0,4]∪[9,+∞).
新知探究
追问3 你还能得到函数y=x+ (k>0)的哪些性质?
(-∞,0)∪(0,+∞),
函数y=x+ (k>0)的定义域为
该函数为奇函数.
它在区间(0, ]上单调递减,
在区间[ ,+∞)上单调递增;
在区间(-∞,- ]上单调递增,
在区间[- ,0)上单调递减.
新知探究
追问4 请你试着画出该函数y=x+ (k>0)的图象.
根据函数性质画出与右图类似的图象.
新知探究
2.单调性与奇偶性的综合应用
新知探究
新知探究
例2 已知函数f(x)是定义域为R的奇函数,当x≥0时,f(x)=x(1+x).画出函数f(x)的图象,并求出函数的解析式.
新知探究
追问1 求f(-1).
f(1)=1×(1+1)=2,
又因为函数f(x)是奇函数,
所以f(-1)=-f(1)=-2.
追问2 求f(t).
当t≥0时,f(t)=t(1+t);
f(-t)=-t×(1+(-t))=-t(1-t),
又因为函数f(x)是奇函数,
所以f(t)=-f(-t)=t(1-t).
当t<0时,-t>0,
例2 已知函数f(x)是定义域为R的奇函数,当x≥0时,f(x)=x(1+x).画出函数f(x)的图象,并求出函数的解析式.
解:当x≥0时,f(x)=x(1+x);
当x<0时,-x>0,f(-x)=-x×(1+(-x))=-x(1-x),
且函数f(x)是奇函数,
所以f(x)=-f(-x)=x(1-x).
综上,f(x)=
图象如图实线部分.
新知探究
追问3 若函数f(x)是定义域为R的偶函数,其他条件不变,画出函数f(x)的图象,并求出函数的解析式.
当x≥0时,f(x)=x(1+x);
当x<0时,-x>0,
f(-x)=-x×(1+(-x))=-x(1-x),
又因为函数f(x)是偶函数,
所以f(x)=f(-x)=-x(1-x)=x(x-1).
图象如图实线部分.
综上,f(x)=
新知探究
追问4 在例2与追问3中,分别判断在(-∞,0)上的单调性,据此你能得到奇函数和偶函数单调性的哪些特点?
例2中,函数在(-∞,0)上单调递增;
追问3中,函数在(-∞,0)上单调递减.
据此得到猜想:
奇函数在对称区间上单调性相同,
偶函数在对称区间上单调性相反.
新知探究
追问5 下面的命题是真命题吗?
已知函数f(x)是偶函数,而且在[a,b]上单调递减,则f(x)在[-b,-a]上单调递增.
如果是请你证明,如果不是,请你举出反例.
这是个真命题.
证明:?x1,x2∈[-b,-a],且x1<x2,
由-b≤x1<x2≤-a,得a≤-x2<-x1≤b,
由f(x)在[a,b]上单调递减,得f(-x2)> f(-x1),
新知探究
追问5 下面的命题是真命题吗?
已知函数f(x)是偶函数,而且在[a,b]上单调递减,则f(x)在[-b,-a]上单调递增.
如果是请你证明,如果不是,请你举出反例.
这是个真命题.
证明:即f(-x1)-f(-x2)<0,
得f(x1)-f(x2)=f(-x1)-f(-x2)<0,
所以,函数f(x)在[-b,-a]上单调递增.
新知探究
(2)应用奇偶性和单调性的定义,我们可以解决什么问题?
(1)如果函数是奇函数,
如果函数是偶函数,
则在对称区间上的单调性是相同的;
则在对称区间上的单调性是相反的.
归纳小结
问题2 回忆本节课的内容,请你回答以下几个问题:
(1)奇偶性与单调性如何互相影响?
问题2 回忆本节课的内容,请你回答以下几个问题:
(1)奇偶性与单调性如何互相影响?
(2)应用奇偶性和单调性的定义,我们可以解决什么问题?
(2)利用单调性定义,
还可以用于判定图象未知的函数的单调性.
可以用于证明一些图象已知的函数的单调性,
利用奇偶性定义,可以判定奇偶性,
归纳小结
还可以解决对称区间上的函数求值问题.
1.已知f(x)= ,x∈R.
目标检测
(1)求证:f(x)在区间[-1,1]上单调递增;
(2)你还能得到函数的哪些性质?
答案:(1)?x1,x2∈[-1,1],且x1<x2,
因为x2-x1>0,x1x2-1<0,所以f(x1)-f(x2)<0,
则f(x1)-f(x2)= ,
1
1.已知f(x)= ,x∈R.
目标检测
(1)求证:f(x)在区间[-1,1]上单调递增;
(2)你还能得到函数的哪些性质?
答案:(1)即f(x1)<f(x2),
(2)①f(x)在区间(-∞,-1]和[1,+∞)上单调递减;
②f(x)是奇函数;③值域为[-1,1].
所以函数f(x)= 在区间[-1,1]上单调递增.
1
2.已知函数f(x)是定义域为R的偶函数,当x<0时,f(x)=x(x+1),则当x>0时,f(x)=____________.
3.函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上单调递减,则a的取值范围是______________.
目标检测
x(x-1)
(-∞,-5]
2
3
再见
问题1 请同学们梳理第3.2节(课本P76~P85)的内容,回答以下几个问题:
复习引入
(1)函数的基本性质有哪些?你能依次从图象特征和代数符号的角度叙述这些性质吗?
(2)你能说说研究函数的性质的方法吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数的性质
单调性
最大(小)值
奇偶性
图象语言
在区间D上,图象从左到右是上升(下降)的,函数值随着自变量的增大而增大(减小).
最高(低)点的纵坐标就是函数f(x)的最大(小)值.
图象关于原点(y轴)对称,则为奇(偶)函数.
符号语言
?x1,x2∈D,当x1<x2时,都有f(x1)<f(x2)(f(x1)>f(x2)),那么就称函数f(x)在区间D上单调递增(递减).
如果存在实数M(m)满足:(1)?x∈I,都有f(x)≤M(f(x)≥m);(2)?x0∈I,使得f(x0)=M(m),那么就称M(m)是函数y=f(x)的最大(小)值.
?x∈I,都有-x∈I,且f(-x)=-f(x)(f(-x)=f(x)),那么函数就叫做奇(偶)函数.
(1)见表
复习引入
复习引入
(2)你能说说研究函数的性质的方法吗?
先观察具体函数图象,分析图象特征,
再结合解析式从代数的角度定量刻画函数性质,抽象出一般概念;
最后应用概念分析解决问题.
形成对函数性质的感性认识;
问题1 请同学们梳理第3.2节(课本P76~P85)的内容,回答以下几个问题:
1.单调性的应用
新知探究
新知探究
(1)根据函数单调性的定义证明函数y=x+ 在区间(3,+∞)上单调递增;
(2)讨论函数y=x+ 在区间(0,+∞)上的单调性;
(3)讨论函数y=x+ (k>0)在区间(0,+∞)上的单调性.
例1(习题3.2 P86第8题)
新知探究
证明:?x1,x2∈(3,+∞),且x1<x2,
有y1-y2=(x1+ )-(x2+ )
=(x1-x2)+( - )
=(x1-x2)+
=(x1-x2)-(1- )
=(x1-x2)( )
例1(习题3.2 P86第8题)
(1)根据函数单调性的定义证明函数y=x+ 在区间(3,+∞)上单调递增;
新知探究
证明:由x1,x2∈(3,+∞),得x1>3,x2>3,
所以x1x2>9,x1x2-9>0.
由x1<x2,得x1-x2<0,
于是(x1-x2)( )<0,即y1<y2.
所以,函数y=x+ 在区间(3,+∞)上的单调递增.
(1)根据函数单调性的定义证明函数y=x+ 在区间(3,+∞)上单调递增;
例1(习题3.2 P86第8题)
新知探究
(2)讨论函数y=x+ 在区间(0,+∞)上的单调性;
解:当x1,x2∈(0,3)时,x1x2-9<0,
在区间(3,+∞)上单调递增.
则y1-y2>0,即y1>y2,
所以y=x+ 在区间(0,3)上单调递减.
综上,y=x+ 在区间(0,3)上单调递减,
例1(习题3.2 P86第8题)
新知探究
(3)讨论函数y=x+ (k>0)在区间(0,+∞)上的单调性.
解:函数y=x+ (k>0)在区间(0, ]上单调递减,
在区间[ ,+∞)上单调递增.
例1(习题3.2 P86第8题)
追问1 判断函数y=x+ (k>0)在区间(0,+∞)上是否存在最值并说明理由;
根据函数y=x+ (k>0)的单调性,
可知该函数在x= 处取到最小值,最小值为2 ,无最大值.
新知探究
追问2 函数y=x+ (k>0)在区间[2,3]上具有单调性,求k的取值范围;
解得:k≥9或0<k≤4,
由该函数的单调性可知:3≤ 或2≥ ,
所以k的取值范围为(0,4]∪[9,+∞).
新知探究
追问3 你还能得到函数y=x+ (k>0)的哪些性质?
(-∞,0)∪(0,+∞),
函数y=x+ (k>0)的定义域为
该函数为奇函数.
它在区间(0, ]上单调递减,
在区间[ ,+∞)上单调递增;
在区间(-∞,- ]上单调递增,
在区间[- ,0)上单调递减.
新知探究
追问4 请你试着画出该函数y=x+ (k>0)的图象.
根据函数性质画出与右图类似的图象.
新知探究
2.单调性与奇偶性的综合应用
新知探究
新知探究
例2 已知函数f(x)是定义域为R的奇函数,当x≥0时,f(x)=x(1+x).画出函数f(x)的图象,并求出函数的解析式.
新知探究
追问1 求f(-1).
f(1)=1×(1+1)=2,
又因为函数f(x)是奇函数,
所以f(-1)=-f(1)=-2.
追问2 求f(t).
当t≥0时,f(t)=t(1+t);
f(-t)=-t×(1+(-t))=-t(1-t),
又因为函数f(x)是奇函数,
所以f(t)=-f(-t)=t(1-t).
当t<0时,-t>0,
例2 已知函数f(x)是定义域为R的奇函数,当x≥0时,f(x)=x(1+x).画出函数f(x)的图象,并求出函数的解析式.
解:当x≥0时,f(x)=x(1+x);
当x<0时,-x>0,f(-x)=-x×(1+(-x))=-x(1-x),
且函数f(x)是奇函数,
所以f(x)=-f(-x)=x(1-x).
综上,f(x)=
图象如图实线部分.
新知探究
追问3 若函数f(x)是定义域为R的偶函数,其他条件不变,画出函数f(x)的图象,并求出函数的解析式.
当x≥0时,f(x)=x(1+x);
当x<0时,-x>0,
f(-x)=-x×(1+(-x))=-x(1-x),
又因为函数f(x)是偶函数,
所以f(x)=f(-x)=-x(1-x)=x(x-1).
图象如图实线部分.
综上,f(x)=
新知探究
追问4 在例2与追问3中,分别判断在(-∞,0)上的单调性,据此你能得到奇函数和偶函数单调性的哪些特点?
例2中,函数在(-∞,0)上单调递增;
追问3中,函数在(-∞,0)上单调递减.
据此得到猜想:
奇函数在对称区间上单调性相同,
偶函数在对称区间上单调性相反.
新知探究
追问5 下面的命题是真命题吗?
已知函数f(x)是偶函数,而且在[a,b]上单调递减,则f(x)在[-b,-a]上单调递增.
如果是请你证明,如果不是,请你举出反例.
这是个真命题.
证明:?x1,x2∈[-b,-a],且x1<x2,
由-b≤x1<x2≤-a,得a≤-x2<-x1≤b,
由f(x)在[a,b]上单调递减,得f(-x2)> f(-x1),
新知探究
追问5 下面的命题是真命题吗?
已知函数f(x)是偶函数,而且在[a,b]上单调递减,则f(x)在[-b,-a]上单调递增.
如果是请你证明,如果不是,请你举出反例.
这是个真命题.
证明:即f(-x1)-f(-x2)<0,
得f(x1)-f(x2)=f(-x1)-f(-x2)<0,
所以,函数f(x)在[-b,-a]上单调递增.
新知探究
(2)应用奇偶性和单调性的定义,我们可以解决什么问题?
(1)如果函数是奇函数,
如果函数是偶函数,
则在对称区间上的单调性是相同的;
则在对称区间上的单调性是相反的.
归纳小结
问题2 回忆本节课的内容,请你回答以下几个问题:
(1)奇偶性与单调性如何互相影响?
问题2 回忆本节课的内容,请你回答以下几个问题:
(1)奇偶性与单调性如何互相影响?
(2)应用奇偶性和单调性的定义,我们可以解决什么问题?
(2)利用单调性定义,
还可以用于判定图象未知的函数的单调性.
可以用于证明一些图象已知的函数的单调性,
利用奇偶性定义,可以判定奇偶性,
归纳小结
还可以解决对称区间上的函数求值问题.
1.已知f(x)= ,x∈R.
目标检测
(1)求证:f(x)在区间[-1,1]上单调递增;
(2)你还能得到函数的哪些性质?
答案:(1)?x1,x2∈[-1,1],且x1<x2,
因为x2-x1>0,x1x2-1<0,所以f(x1)-f(x2)<0,
则f(x1)-f(x2)= ,
1
1.已知f(x)= ,x∈R.
目标检测
(1)求证:f(x)在区间[-1,1]上单调递增;
(2)你还能得到函数的哪些性质?
答案:(1)即f(x1)<f(x2),
(2)①f(x)在区间(-∞,-1]和[1,+∞)上单调递减;
②f(x)是奇函数;③值域为[-1,1].
所以函数f(x)= 在区间[-1,1]上单调递增.
1
2.已知函数f(x)是定义域为R的偶函数,当x<0时,f(x)=x(x+1),则当x>0时,f(x)=____________.
3.函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上单调递减,则a的取值范围是______________.
目标检测
x(x-1)
(-∞,-5]
2
3
再见
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
