13.3 乘法公式(第3课时 两数和的平方)
文档属性
| 名称 | 13.3 乘法公式(第3课时 两数和的平方) |

|
|
| 格式 | rar | ||
| 文件大小 | 344.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-14 11:12:54 | ||
图片预览


文档简介
(共9张PPT)
标题
标题
华东师大版八年级(上册)
第13章 整式的乘除
13.3 乘法公式(第3课时)
a2 b2
平方差公式
回顾 & 思考
(a+b)(a b)=
练习:
( x + 2y )( x – 2y) = ______
(mn – 3)(mn +3)= ______
(– 2x+y)(2x+y)= ______
x2 –4y2
m2n2 –9
y2 –4x2
多项式的乘法
(a+b)(c+d)
ac
ad
bc
bd
=
+
+
+
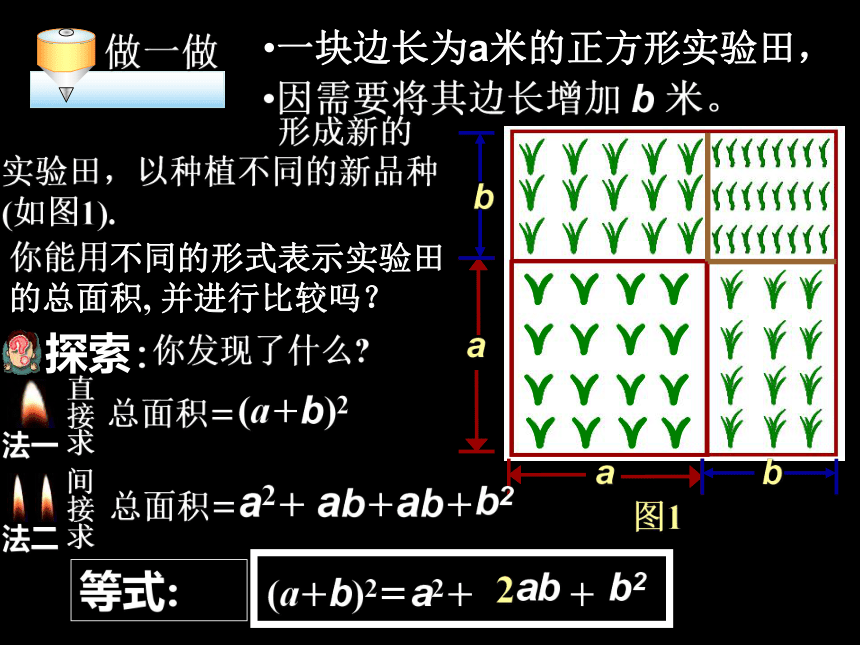
做一做
图1
a
一块边长为a米的正方形实验田,
因需要将其边长增加 b 米。
形成新的实验田,以种植不同的新品种(如图1).
你能用不同的形式表示实验田的总面积, 并进行比较吗?
a
b
b
法一
直
接
求
总面积=
(a+b)2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2
(a+b)2=
a2+
ab
+
b2
你发现了什么
探索:
2
等式:
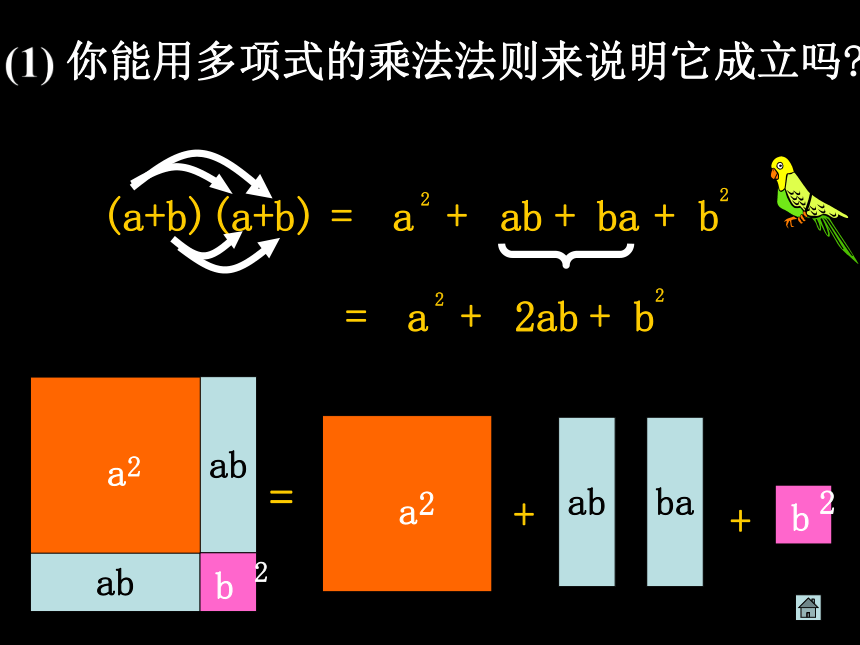
(a+b)(a+b)
ab
ba
=
+
+
+
ab
ab
a
2
b
2
a
2
b
2
a
2
=
ab
ba
b
2
+
+
2ab
=
+
+
a
2
b
2
(1) 你能用多项式的乘法法则来说明它成立吗
他们是怎么想的 想法对吗?你会如何解决这个问题?
利用两数和的
平方
推证
(a b)2=
[a+( b)]2
= + +__
a2
2a
( b)
( b)2
=
a2
2ab
b2.
+
(2)
有两位同学对两数差的平方有不同的看法:
乙:(a b)2
动脑筋
想一想
(a+b)2=a2+2ab+b2 ;
a2 2ab+b2.
(a b)2=
= a 2 + 2a( b) + ( b) 2
甲:(a b)2
= a 2 b 2
初 识 完全平方公式
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
结构特征:
左边是
的平方;
右边是
两数和
(差)
两数的平方和
加上
(减去)
这两数乘积的两倍.
用自己的语言叙述上面的公式
语言表述:
两数和 的平方
等于这两数的平方和
加上 这两数乘积的两倍.
(差)
(减去)
注意:
1.完全平方公式和平方差公式的区别!
2. (a + b )2≠a2 + b2
(a – b )2 ≠a2 – b2
(a + b ) (a – b ) ﹦ a2 – b2
2
2
a+b
a b
a2 +b2
a2 +b2
+
2ab
2ab
( 2x )2 2 2x 3 +32
解:(1) (2x 3)2
=
例 利用完全平方公式计算:
(1) (2x 3)2 ; (2) (4x+5y)2 ; (3) (m n a)2
注意
先明确用哪个完全平方公式
再把计算的式子与完全平方公式对照, 明确哪个是 a , 哪个是 b.
4x2
=
12x
+
9 ;
(2) (4x + 5y )2
= (4x)2 + 2 · 4x · 5y + (5y)2
=16 x2 + 40 x y +25y2
(3) ( m n a )2
= ( m n )2 2 · m n · a + a2
= m2 n2 2 m n a + a2
( a b )2= a2 2 a b + b2
( 2 x 3 )2
=
(2x)2
2·2x· 3
+32
随堂练习
说出下列各式中的错误,并加以改正:
(1) (2a 1)2=2a2 2a+1;
(2) (2a+1)2=4a2 +1;
(3) ( a 1)2= a2 2a 1.
解:
(1)(2a 1)2= (2a)2 2 2a 1 +1=4a2 4a +1
(2)(2a+1)2= (2a)2+2 2a 1 +1=4a2 + 4a +1
(3)( a 1)2=( a)2 2 ( a) 1 + 1=a2 + 2a + 1
学会了什么知识?
知道了什么思想方法?
还有什么问题?
标题
标题
华东师大版八年级(上册)
第13章 整式的乘除
13.3 乘法公式(第3课时)
a2 b2
平方差公式
回顾 & 思考
(a+b)(a b)=
练习:
( x + 2y )( x – 2y) = ______
(mn – 3)(mn +3)= ______
(– 2x+y)(2x+y)= ______
x2 –4y2
m2n2 –9
y2 –4x2
多项式的乘法
(a+b)(c+d)
ac
ad
bc
bd
=
+
+
+
做一做
图1
a
一块边长为a米的正方形实验田,
因需要将其边长增加 b 米。
形成新的实验田,以种植不同的新品种(如图1).
你能用不同的形式表示实验田的总面积, 并进行比较吗?
a
b
b
法一
直
接
求
总面积=
(a+b)2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2
(a+b)2=
a2+
ab
+
b2
你发现了什么
探索:
2
等式:
(a+b)(a+b)
ab
ba
=
+
+
+
ab
ab
a
2
b
2
a
2
b
2
a
2
=
ab
ba
b
2
+
+
2ab
=
+
+
a
2
b
2
(1) 你能用多项式的乘法法则来说明它成立吗
他们是怎么想的 想法对吗?你会如何解决这个问题?
利用两数和的
平方
推证
(a b)2=
[a+( b)]2
= + +__
a2
2a
( b)
( b)2
=
a2
2ab
b2.
+
(2)
有两位同学对两数差的平方有不同的看法:
乙:(a b)2
动脑筋
想一想
(a+b)2=a2+2ab+b2 ;
a2 2ab+b2.
(a b)2=
= a 2 + 2a( b) + ( b) 2
甲:(a b)2
= a 2 b 2
初 识 完全平方公式
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
结构特征:
左边是
的平方;
右边是
两数和
(差)
两数的平方和
加上
(减去)
这两数乘积的两倍.
用自己的语言叙述上面的公式
语言表述:
两数和 的平方
等于这两数的平方和
加上 这两数乘积的两倍.
(差)
(减去)
注意:
1.完全平方公式和平方差公式的区别!
2. (a + b )2≠a2 + b2
(a – b )2 ≠a2 – b2
(a + b ) (a – b ) ﹦ a2 – b2
2
2
a+b
a b
a2 +b2
a2 +b2
+
2ab
2ab
( 2x )2 2 2x 3 +32
解:(1) (2x 3)2
=
例 利用完全平方公式计算:
(1) (2x 3)2 ; (2) (4x+5y)2 ; (3) (m n a)2
注意
先明确用哪个完全平方公式
再把计算的式子与完全平方公式对照, 明确哪个是 a , 哪个是 b.
4x2
=
12x
+
9 ;
(2) (4x + 5y )2
= (4x)2 + 2 · 4x · 5y + (5y)2
=16 x2 + 40 x y +25y2
(3) ( m n a )2
= ( m n )2 2 · m n · a + a2
= m2 n2 2 m n a + a2
( a b )2= a2 2 a b + b2
( 2 x 3 )2
=
(2x)2
2·2x· 3
+32
随堂练习
说出下列各式中的错误,并加以改正:
(1) (2a 1)2=2a2 2a+1;
(2) (2a+1)2=4a2 +1;
(3) ( a 1)2= a2 2a 1.
解:
(1)(2a 1)2= (2a)2 2 2a 1 +1=4a2 4a +1
(2)(2a+1)2= (2a)2+2 2a 1 +1=4a2 + 4a +1
(3)( a 1)2=( a)2 2 ( a) 1 + 1=a2 + 2a + 1
学会了什么知识?
知道了什么思想方法?
还有什么问题?
