沪科版七年级上册数学3.5 三元一次方程组及其解法课件(16张PPT)
文档属性
| 名称 | 沪科版七年级上册数学3.5 三元一次方程组及其解法课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 213.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 13:43:54 | ||
图片预览





文档简介
3.5 三元一次方程组及其解法
1.
(1)根据特点说说你选择什么解法
(2)什么是二元一次方程组?
解二元一次方程组主要思想方法是什么?
加减消元
代入消元
二元一次方程组
一元一次方程
复习
2.
问题:甲、乙、丙三数的和是26,甲数比乙数大1,甲数的两倍与丙数的和比乙数大18,求这三个数.
思考:题目中有几个未知数?含有几个相等关系?你能根据题意列出几个方程?
列式:
设甲数为x.乙数为y,丙数为z
问题引入
方程组
三元一次方程组:
由三个一次方程组成的含有三个未知数的方程组.叫做三元一次方程组
讨论:上面方程组具有什么特点(给它起个名)
下面方程组那些是三元一次方程组
代入消元
一元一次
方程
加减消元
二元一次
方程组
代入消元
加减消元
三元一次
方程组
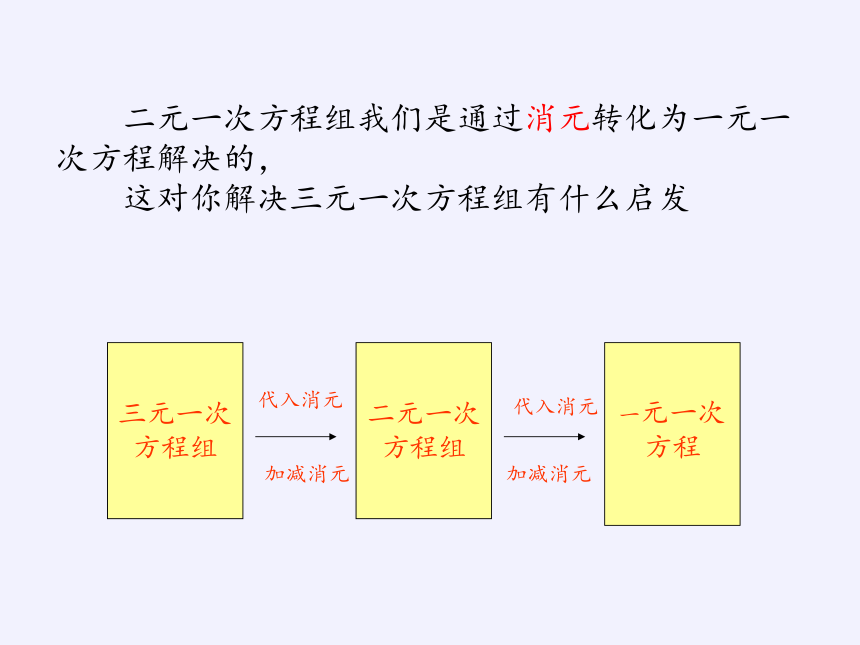
二元一次方程组我们是通过消元转化为一元一次方程解决的,
这对你解决三元一次方程组有什么启发
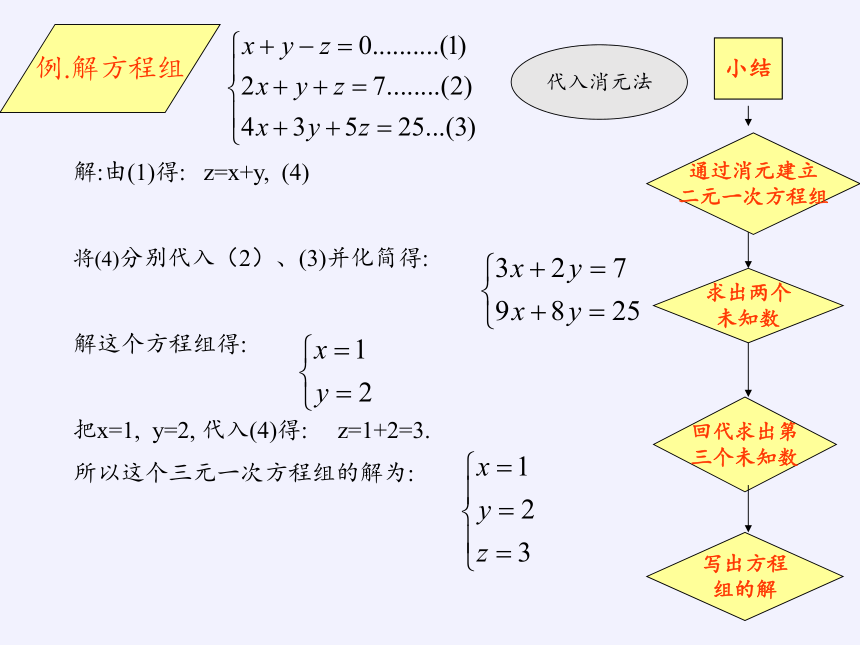
解:由(1)得: z=x+y, (4)
将(4)分别代入(2)、(3)并化简得:
解这个方程组得:
把x=1, y=2, 代入(4)得: z=1+2=3.
所以这个三元一次方程组的解为:
代入消元法
求出两个
未知数
回代求出第
三个未知数
写出方程
组的解
小结
通过消元建立
二元一次方程组
小结
例.解方程组
解:由(1)+(2)得: 3x+2y=7, (4)
由(1) 5+ (3)得:9x+8y=25 (5)
将(4)(5)组成方程组得:
解这个方程组得:
把x=1, y=2, 代入(1)得: 1+2-z=0, z=3.
所以这个三元一次方程组的解为:
×
加减消元法
小结
通过消元建立
二元一次方程组
求出两个
未知数
回代求出第
三个未知数
写出方程
组的解
例.解方程组
解:由(1) 2+(2)得: y+5z=3, (4)
由(3)-(1)得:y-6z=-8 (5)
将(4)(5)组成方程组得:
解这个方程组得:
把y=-2, z=1, 代入(1)得: x-2+2=3, x=3.
所以这个三元一次方程组的解为:
×
先讨论
如何消元
建立二元一
次方程组
试解方程组
例.在等式 中,当x=-1时,y=0;当x=2 时,y=3; 当x=5时,y=60.求a,b,c的值.
解:根据题意:得
(2)-(1)得. a+b=1. (4)
(3)-(1)得: 4a+b=10. (5)
(4)与(5)组成方程组
解这个方程组得:
把 代入(1)得:c=-5
因此:
学以致用
(1)解二元一次方程组的基本方法是代入法和加减法,其中加减法比较常用.
(2)解三元一次方程组的基本思想是消元,关键也是消元,我们一定要根据方程组的特点,选准消元对象,定好消元方案.
(3)解完后要代入原方程组的三个方程中进行检验.
小 结
解:因为三个非负数的和等于零.所以每个非负数都为零.可得方程组:
解这个方程组得:
练
习
解方程组
注意:应重在化难为易的思考过程分析.
作业
习题3.5: 第1、2、3、4题
思考题
例.某学校中的篮球数比排球数的2倍少3,足球数与排球数的比是2:3,三种球共41个.求三种球各是多少个. 解:设篮球有X个,排球有Y个,足球有Z个. 根据题意,得:
把(1)代入(3)得;3y+z=44.(4) 由(4)得:z=44-3 (5). 把(5)代入(2),得:y=12. 把y=12 分别代入(1),(5).得:x=21,z=8. 所以这个方程组的解是:
谢 谢
1.
(1)根据特点说说你选择什么解法
(2)什么是二元一次方程组?
解二元一次方程组主要思想方法是什么?
加减消元
代入消元
二元一次方程组
一元一次方程
复习
2.
问题:甲、乙、丙三数的和是26,甲数比乙数大1,甲数的两倍与丙数的和比乙数大18,求这三个数.
思考:题目中有几个未知数?含有几个相等关系?你能根据题意列出几个方程?
列式:
设甲数为x.乙数为y,丙数为z
问题引入
方程组
三元一次方程组:
由三个一次方程组成的含有三个未知数的方程组.叫做三元一次方程组
讨论:上面方程组具有什么特点(给它起个名)
下面方程组那些是三元一次方程组
代入消元
一元一次
方程
加减消元
二元一次
方程组
代入消元
加减消元
三元一次
方程组
二元一次方程组我们是通过消元转化为一元一次方程解决的,
这对你解决三元一次方程组有什么启发
解:由(1)得: z=x+y, (4)
将(4)分别代入(2)、(3)并化简得:
解这个方程组得:
把x=1, y=2, 代入(4)得: z=1+2=3.
所以这个三元一次方程组的解为:
代入消元法
求出两个
未知数
回代求出第
三个未知数
写出方程
组的解
小结
通过消元建立
二元一次方程组
小结
例.解方程组
解:由(1)+(2)得: 3x+2y=7, (4)
由(1) 5+ (3)得:9x+8y=25 (5)
将(4)(5)组成方程组得:
解这个方程组得:
把x=1, y=2, 代入(1)得: 1+2-z=0, z=3.
所以这个三元一次方程组的解为:
×
加减消元法
小结
通过消元建立
二元一次方程组
求出两个
未知数
回代求出第
三个未知数
写出方程
组的解
例.解方程组
解:由(1) 2+(2)得: y+5z=3, (4)
由(3)-(1)得:y-6z=-8 (5)
将(4)(5)组成方程组得:
解这个方程组得:
把y=-2, z=1, 代入(1)得: x-2+2=3, x=3.
所以这个三元一次方程组的解为:
×
先讨论
如何消元
建立二元一
次方程组
试解方程组
例.在等式 中,当x=-1时,y=0;当x=2 时,y=3; 当x=5时,y=60.求a,b,c的值.
解:根据题意:得
(2)-(1)得. a+b=1. (4)
(3)-(1)得: 4a+b=10. (5)
(4)与(5)组成方程组
解这个方程组得:
把 代入(1)得:c=-5
因此:
学以致用
(1)解二元一次方程组的基本方法是代入法和加减法,其中加减法比较常用.
(2)解三元一次方程组的基本思想是消元,关键也是消元,我们一定要根据方程组的特点,选准消元对象,定好消元方案.
(3)解完后要代入原方程组的三个方程中进行检验.
小 结
解:因为三个非负数的和等于零.所以每个非负数都为零.可得方程组:
解这个方程组得:
练
习
解方程组
注意:应重在化难为易的思考过程分析.
作业
习题3.5: 第1、2、3、4题
思考题
例.某学校中的篮球数比排球数的2倍少3,足球数与排球数的比是2:3,三种球共41个.求三种球各是多少个. 解:设篮球有X个,排球有Y个,足球有Z个. 根据题意,得:
把(1)代入(3)得;3y+z=44.(4) 由(4)得:z=44-3 (5). 把(5)代入(2),得:y=12. 把y=12 分别代入(1),(5).得:x=21,z=8. 所以这个方程组的解是:
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
