沪科版七年级上册数学4.4 角课件(25张PPT)
文档属性
| 名称 | 沪科版七年级上册数学4.4 角课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 774.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览






文档简介
4.4 角
学习目标
1.通过丰富的实例,理解角的形成,建立几何中角的概念。
2.掌握角的两种定义形式和四种表示方法。
3.理解平角、周角的概念,通过对平角和周角的理解,更加深入的掌握角的两种定义。
教学重点与难点
重点:角的概念与角的表示方法
难点:正确理解角的概念
角的定义
什么是角呢?
生活中有许多与角有关的实例,观察下图,你能指出图中的角吗?
一、创设情境,引入新知
Back
1
2
3
4
5
6
7
8
9
10
11
12
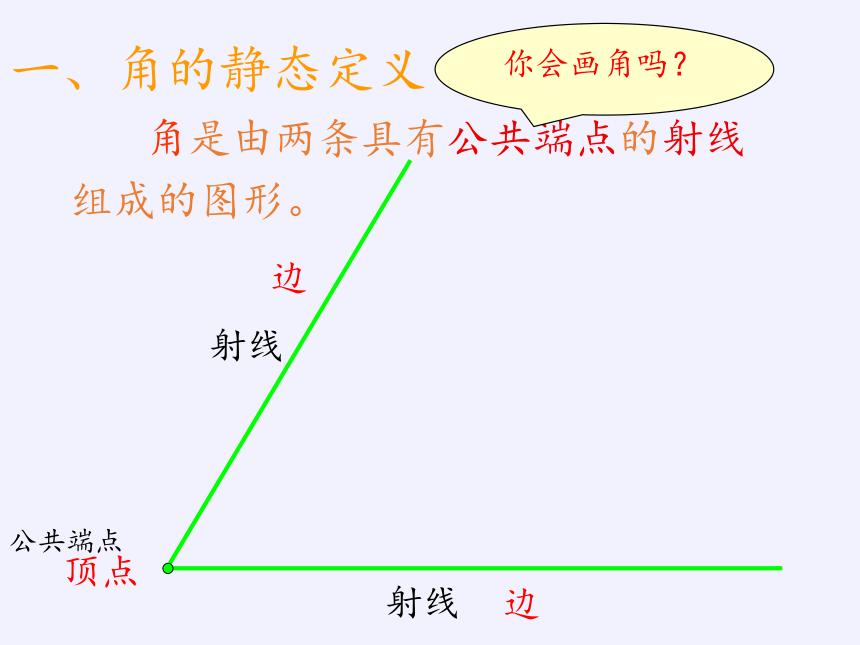
角是由两条具有公共端点的射线
组成的图形。
公共端点
顶点
射线
射线
边
边
一、角的静态定义
你会画角吗?
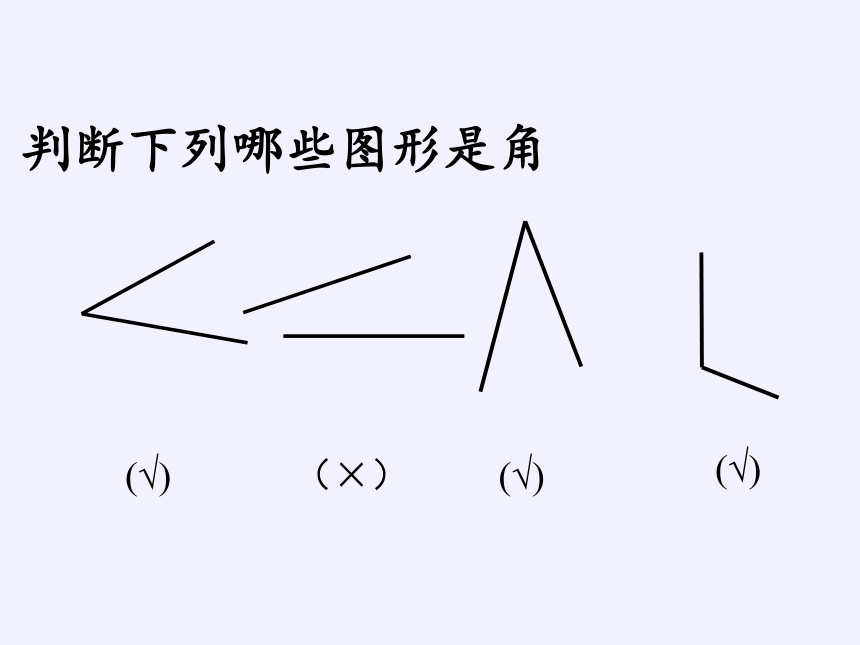
判断下列哪些图形是角
(√)
(√)
(√)
(×)
二、角的表示方法
O
A
B
O
α
O
1
③记作:∠AOB 或∠BOA
②记作∠α
①记作∠1
④或∠O
问题
1.如图,能把∠α记作∠O吗?
∠α还可以怎么表示?
A
O
C
B
α
)
)
β
2.在上图中共有几个角?分别把他们读出来。
牛刀小试
3、把图中的角表示成下列形式:
①∠APO ②∠AOP ③∠OPC,
④∠O ⑤∠COP ⑥∠P
其中正确的有 (把你认为正确的序号都填上。)
P
O
A
C
① ③ ⑥
4、将图中的角用不同的方法表示出来,
并填写下表
∠1
∠3
∠4
∠ACB
∠ABC
A
D
C
B
E
5
4
3
1
2
∠BCE
∠2
∠BAC
∠DAB
∠5
A
O
B
角也可以看做一条射线绕端点旋转所组成的图形。
三、角的动态定义
始边
终边
(一)平角
1. 问题:平角是什么样的呢?你们能动手画一画平角吗?
四、认识平角和周角
2. 问题:你能用自己的话说一说平角是怎样形成的吗?
3. 小结:通过观察我们发现平角是由一条射线绕它的端点旋转,当成一条直线时就形成了平角。
4. 问题:平角的角到底在哪里?画出角的符号。
5. 追问:平角是多少度呢?(板书:1平角=180°)
(二)周角
1. 问题:请你想象一下周角是什么样的, 然后在练习本上画一画。
2. 问题:怎么只看到一条边呢?这还是角吗?
因为一条射线绕它的端点旋转一周,最后两射线重合在一起了。
3. 追问:周角的角在哪里?
4. 追问:周角是多少度呢?(板书:1周角=360°)
五、巩固练习,内化提升
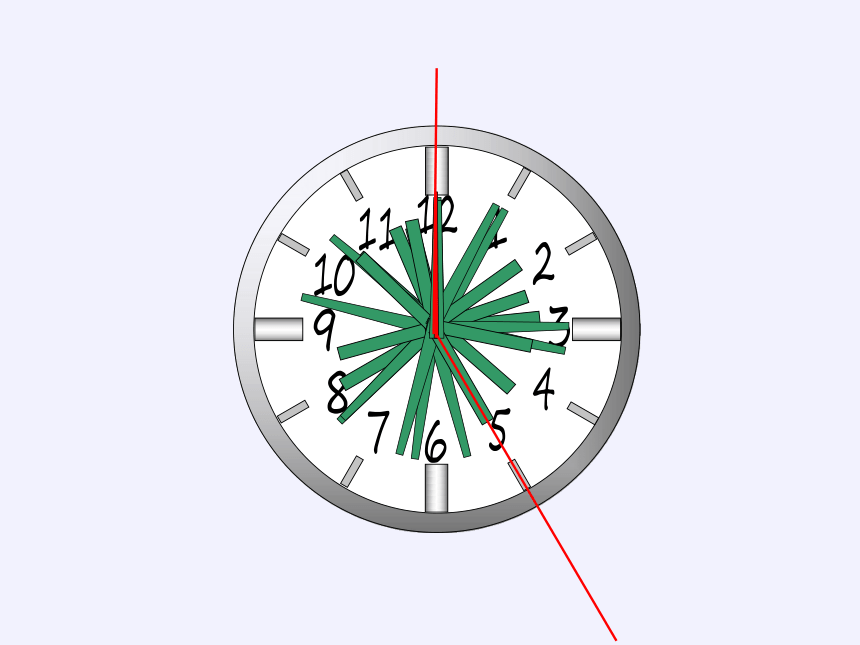
1. 说出每个钟面上时针和分针所构成的角的名称。
2、练一练
C
D
B
A
(1)∠ABD与∠ABC是同一个角吗?
(2)能用一个大写字母表示的角有几个?
(3)以点A为顶点的角有哪几个?
以点D为顶点的角呢?
(4)图中共有多少个角?是哪些角?
3、如图1, D、E分别是AB、AC上的点.
∠ ABC与∠ DBC是不是同一个角?
∠BAC与∠ DAE是不是同一个角?
∠BAC与∠ ACB是不是同一个角?
4、如图2,图中共有多少个角?请分别表示它们。
D
E
A
C
B
图1
O
A
D
E
C
B
图2
5、如图3,用大写字母表示图中用希腊字母标注的角。
∠ α =___ ∠ β=____
∠ γ =___ ∠ θ=_____
A
C
B
图3
D
E
F
γ
β
α
θ
六、课堂小结
通过这节课你学到了什么?
七、布置作业
作业:第144页练习第1、2题。
第145页习题4.4第1题。
谢 谢
学习目标
1.通过丰富的实例,理解角的形成,建立几何中角的概念。
2.掌握角的两种定义形式和四种表示方法。
3.理解平角、周角的概念,通过对平角和周角的理解,更加深入的掌握角的两种定义。
教学重点与难点
重点:角的概念与角的表示方法
难点:正确理解角的概念
角的定义
什么是角呢?
生活中有许多与角有关的实例,观察下图,你能指出图中的角吗?
一、创设情境,引入新知
Back
1
2
3
4
5
6
7
8
9
10
11
12
角是由两条具有公共端点的射线
组成的图形。
公共端点
顶点
射线
射线
边
边
一、角的静态定义
你会画角吗?
判断下列哪些图形是角
(√)
(√)
(√)
(×)
二、角的表示方法
O
A
B
O
α
O
1
③记作:∠AOB 或∠BOA
②记作∠α
①记作∠1
④或∠O
问题
1.如图,能把∠α记作∠O吗?
∠α还可以怎么表示?
A
O
C
B
α
)
)
β
2.在上图中共有几个角?分别把他们读出来。
牛刀小试
3、把图中的角表示成下列形式:
①∠APO ②∠AOP ③∠OPC,
④∠O ⑤∠COP ⑥∠P
其中正确的有 (把你认为正确的序号都填上。)
P
O
A
C
① ③ ⑥
4、将图中的角用不同的方法表示出来,
并填写下表
∠1
∠3
∠4
∠ACB
∠ABC
A
D
C
B
E
5
4
3
1
2
∠BCE
∠2
∠BAC
∠DAB
∠5
A
O
B
角也可以看做一条射线绕端点旋转所组成的图形。
三、角的动态定义
始边
终边
(一)平角
1. 问题:平角是什么样的呢?你们能动手画一画平角吗?
四、认识平角和周角
2. 问题:你能用自己的话说一说平角是怎样形成的吗?
3. 小结:通过观察我们发现平角是由一条射线绕它的端点旋转,当成一条直线时就形成了平角。
4. 问题:平角的角到底在哪里?画出角的符号。
5. 追问:平角是多少度呢?(板书:1平角=180°)
(二)周角
1. 问题:请你想象一下周角是什么样的, 然后在练习本上画一画。
2. 问题:怎么只看到一条边呢?这还是角吗?
因为一条射线绕它的端点旋转一周,最后两射线重合在一起了。
3. 追问:周角的角在哪里?
4. 追问:周角是多少度呢?(板书:1周角=360°)
五、巩固练习,内化提升
1. 说出每个钟面上时针和分针所构成的角的名称。
2、练一练
C
D
B
A
(1)∠ABD与∠ABC是同一个角吗?
(2)能用一个大写字母表示的角有几个?
(3)以点A为顶点的角有哪几个?
以点D为顶点的角呢?
(4)图中共有多少个角?是哪些角?
3、如图1, D、E分别是AB、AC上的点.
∠ ABC与∠ DBC是不是同一个角?
∠BAC与∠ DAE是不是同一个角?
∠BAC与∠ ACB是不是同一个角?
4、如图2,图中共有多少个角?请分别表示它们。
D
E
A
C
B
图1
O
A
D
E
C
B
图2
5、如图3,用大写字母表示图中用希腊字母标注的角。
∠ α =___ ∠ β=____
∠ γ =___ ∠ θ=_____
A
C
B
图3
D
E
F
γ
β
α
θ
六、课堂小结
通过这节课你学到了什么?
七、布置作业
作业:第144页练习第1、2题。
第145页习题4.4第1题。
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
