沪科版八年级上册 数学 课件: 11.1平面内点的坐标(15张)
文档属性
| 名称 | 沪科版八年级上册 数学 课件: 11.1平面内点的坐标(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 275.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览




文档简介
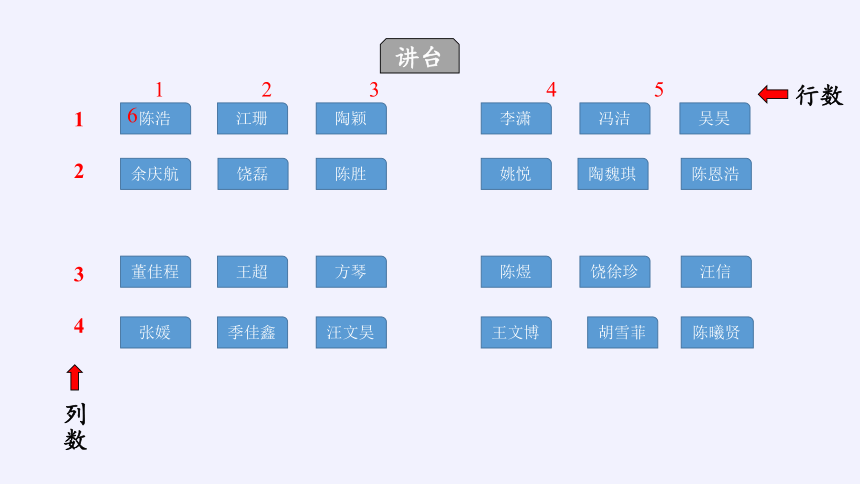
平面内点的坐标
讲台
行数
列数
陈浩
江珊
陶颖
李潇
冯洁
吴昊
余庆航
饶磊
陈胜
陈恩浩
陶魏琪
姚悦
方琴
王超
董佳程
张媛
季佳鑫
汪文昊
汪信
饶徐珍
陈煜
王文博
胡雪菲
陈曦贤
1
2
3
4
5
6
1
2
3
4
生活中的数学
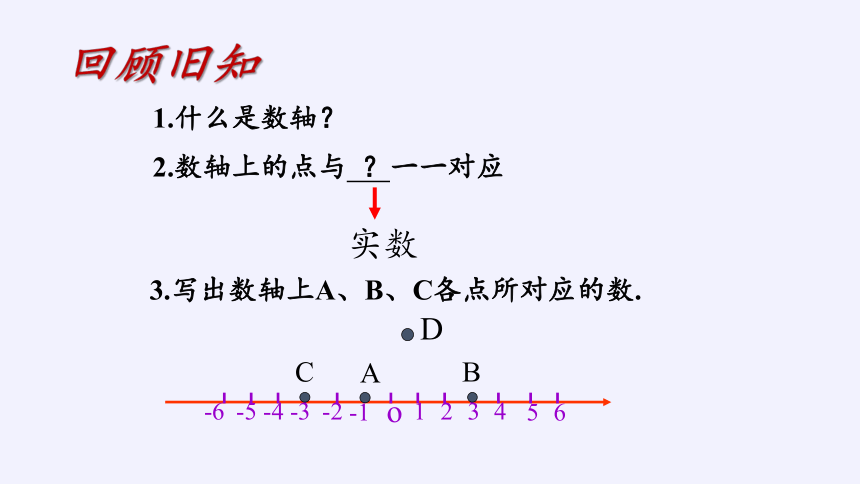
1.什么是数轴?
2.数轴上的点与
?一一对应
实数
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
A
B
C
3.写出数轴上A、B、C各点所对应的数.
D
回顾旧知
平面内,两条互相垂直且原点重合的数
轴就构成平面直角坐标系,简称直角坐标系。
水平的数轴称为x轴或横轴。
竖直的数轴称为y轴或纵轴。
两数轴的交点O称为坐标原点。
建立了直角坐标系的平面叫做坐标平面。
Zx
y
x
o
20
10
10
-10
-20
-30
20
30
-20
-10
-40
-50
概念学习
坐标轴
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
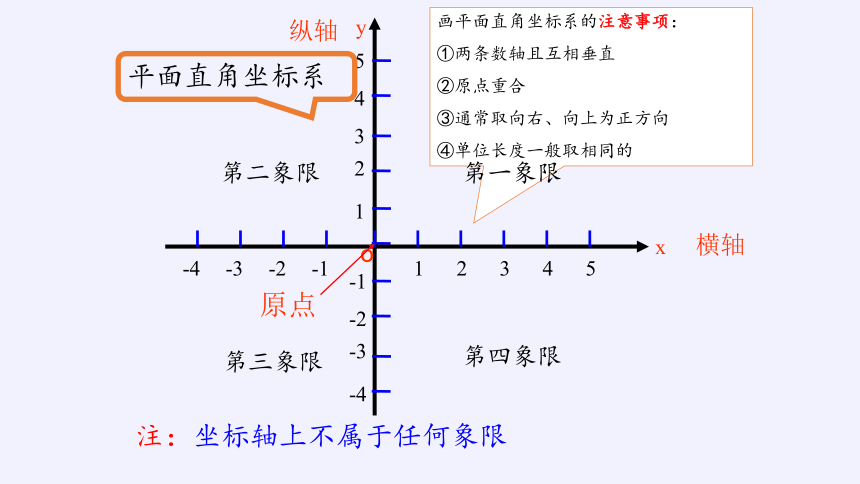
画平面直角坐标系的注意事项:
①两条数轴且互相垂直
②原点重合
③通常取向右、向上为正方向
④单位长度一般取相同的
平面直角坐标系
注:坐标轴上不属于任何象限
第一象限
第二象限
第三象限
第四象限
y
-5
-6
横坐标
纵坐标
x
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
1
2
3
4
5
-1
-2
-3
-4
(
3
,
4
)
A
如图,A是直角坐标系中一点,你能找到其对应的有序实数对吗?
.
先横后纵
有序实数对(3,4)叫做点A在平面直角坐标系中的坐标。
写出图中各
点的坐标:
A
(
,
)
B
(
,
)
C
(
,
)
D
(
,
)
-2
2
-3
-1
3
1
-2
2
例
1
O
-1
-2
-3
1
2
3
1
2
3
-1
-2
-3
x
4
y
A
B
D
C
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
已知各点的坐标,请在直角坐标系中找出点的位置:
A(2,3)
B(3,2)
C(-2,1)
D(-4,-3)
E(1,-2)
探究1
想一想:(2,3)与(3,2)表示同一个点吗?
平面内的点与有序实数对一一对应!
(+,+)
(-,+)
(-
,-)
(+,-)
探究2
各象限内点的坐标有何特征?
陈浩
江珊
陶颖
李潇
冯洁
吴昊
余庆航
饶磊
陈胜
陈恩浩
陶魏琪
姚悦
方琴
王超
董佳程
张媛
季佳鑫
汪文昊
汪信
饶徐珍
陈煜
王文博
胡雪菲
陈曦贤
O
-1
-2
-3
1
2
3
X
1
2
-1
-2
y
A
B
C
D
(3,0)
(-4,0)
(0,5)
(0,-4)
(0,0)
坐标轴上点有何特征?
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
探究3
在y轴上的点,
横坐标等于0.
在x轴上的点,
纵坐标等于0.
1、已知P点坐标为(a-1,a-5)
①点P在x轴上,则a=
;
②点P在y轴上,则a=
;
③若a=-3
,则点P在第
象限;
④若a=3,则点P在第
象限.
2、若点P(x,y)在第四象限,|x|=2,
|y|=3,则P点的坐标为
.
5
(2,-3)
1
三
四
一展身手
本节课我们学面直角坐标系,学习本节我们要掌握以下三方面的知识内容:
1.能够正确画出直角坐标系.
2.能在直角坐标系中,根据坐标找出点,由点求出坐标.理解坐标平面内的点和有序实数对一一对应的.
3.掌握象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
课堂小结
已知三点A(0,4)、B(-3,0)、C(3,0)现以A、B、C为顶点画平行四边形,写出符合条件的D点坐标.
课后思考
谢
谢
讲台
行数
列数
陈浩
江珊
陶颖
李潇
冯洁
吴昊
余庆航
饶磊
陈胜
陈恩浩
陶魏琪
姚悦
方琴
王超
董佳程
张媛
季佳鑫
汪文昊
汪信
饶徐珍
陈煜
王文博
胡雪菲
陈曦贤
1
2
3
4
5
6
1
2
3
4
生活中的数学
1.什么是数轴?
2.数轴上的点与
?一一对应
实数
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
A
B
C
3.写出数轴上A、B、C各点所对应的数.
D
回顾旧知
平面内,两条互相垂直且原点重合的数
轴就构成平面直角坐标系,简称直角坐标系。
水平的数轴称为x轴或横轴。
竖直的数轴称为y轴或纵轴。
两数轴的交点O称为坐标原点。
建立了直角坐标系的平面叫做坐标平面。
Zx
y
x
o
20
10
10
-10
-20
-30
20
30
-20
-10
-40
-50
概念学习
坐标轴
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
画平面直角坐标系的注意事项:
①两条数轴且互相垂直
②原点重合
③通常取向右、向上为正方向
④单位长度一般取相同的
平面直角坐标系
注:坐标轴上不属于任何象限
第一象限
第二象限
第三象限
第四象限
y
-5
-6
横坐标
纵坐标
x
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
1
2
3
4
5
-1
-2
-3
-4
(
3
,
4
)
A
如图,A是直角坐标系中一点,你能找到其对应的有序实数对吗?
.
先横后纵
有序实数对(3,4)叫做点A在平面直角坐标系中的坐标。
写出图中各
点的坐标:
A
(
,
)
B
(
,
)
C
(
,
)
D
(
,
)
-2
2
-3
-1
3
1
-2
2
例
1
O
-1
-2
-3
1
2
3
1
2
3
-1
-2
-3
x
4
y
A
B
D
C
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
C
·
A
·
E
·
D
(
2,3
)
(
3,2
)
(
-2,1
)
(
-4,-
3
)
(
1,-
2
)
已知各点的坐标,请在直角坐标系中找出点的位置:
A(2,3)
B(3,2)
C(-2,1)
D(-4,-3)
E(1,-2)
探究1
想一想:(2,3)与(3,2)表示同一个点吗?
平面内的点与有序实数对一一对应!
(+,+)
(-,+)
(-
,-)
(+,-)
探究2
各象限内点的坐标有何特征?
陈浩
江珊
陶颖
李潇
冯洁
吴昊
余庆航
饶磊
陈胜
陈恩浩
陶魏琪
姚悦
方琴
王超
董佳程
张媛
季佳鑫
汪文昊
汪信
饶徐珍
陈煜
王文博
胡雪菲
陈曦贤
O
-1
-2
-3
1
2
3
X
1
2
-1
-2
y
A
B
C
D
(3,0)
(-4,0)
(0,5)
(0,-4)
(0,0)
坐标轴上点有何特征?
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
探究3
在y轴上的点,
横坐标等于0.
在x轴上的点,
纵坐标等于0.
1、已知P点坐标为(a-1,a-5)
①点P在x轴上,则a=
;
②点P在y轴上,则a=
;
③若a=-3
,则点P在第
象限;
④若a=3,则点P在第
象限.
2、若点P(x,y)在第四象限,|x|=2,
|y|=3,则P点的坐标为
.
5
(2,-3)
1
三
四
一展身手
本节课我们学面直角坐标系,学习本节我们要掌握以下三方面的知识内容:
1.能够正确画出直角坐标系.
2.能在直角坐标系中,根据坐标找出点,由点求出坐标.理解坐标平面内的点和有序实数对一一对应的.
3.掌握象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
课堂小结
已知三点A(0,4)、B(-3,0)、C(3,0)现以A、B、C为顶点画平行四边形,写出符合条件的D点坐标.
课后思考
谢
谢
