沪科版八年级上册 数学 14.2 三角形全等的判定课件(16张PPT)
文档属性
| 名称 | 沪科版八年级上册 数学 14.2 三角形全等的判定课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 462.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-26 00:00:00 | ||
图片预览



文档简介
14.2 三角形全等的判定
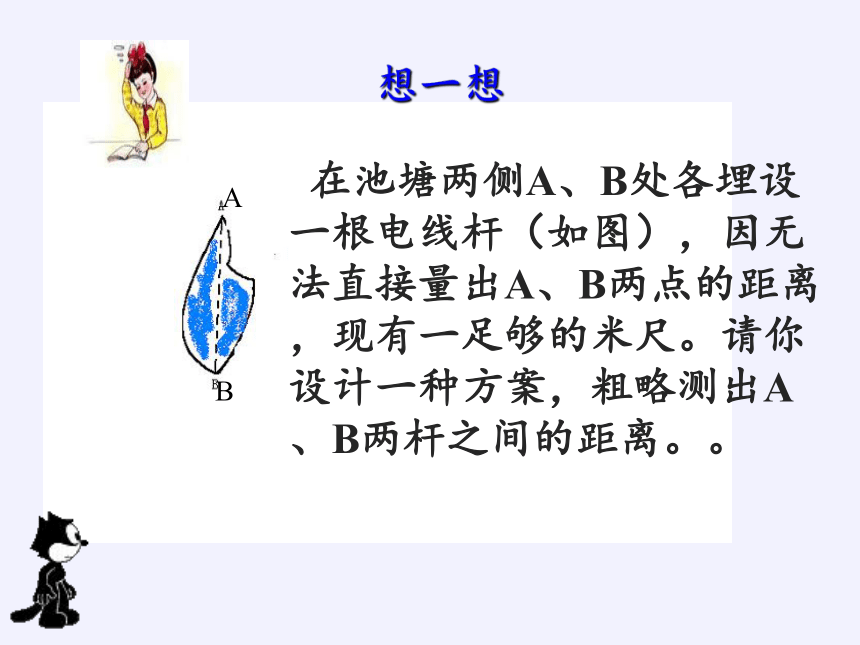
想一想
在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。
A
B
教材97-98,一个条件可以吗?
1有一条边相等的两个三角形不一定全等
议一议
2. 有一个角相等的两个三角形
不一定全等
结论:
有一个条件相等不能保证两个三角形全等.
6cm
300
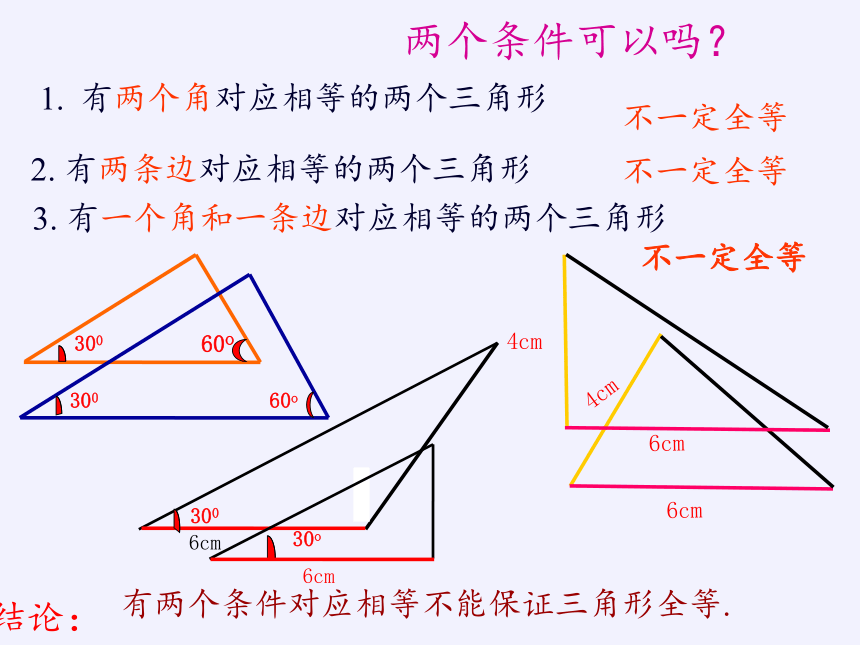
有两个条件对应相等不能保证三角形全等.
60o
300
不一定全等
有两个角对应相等的两个三角形
两个条件可以吗?
3. 有一个角和一条边对应相等的两个三角形
2. 有两条边对应相等的两个三角形
4cm
6cm
不一定全等
300
60o
4cm
6cm
不一定全等
30o
6cm
结论:
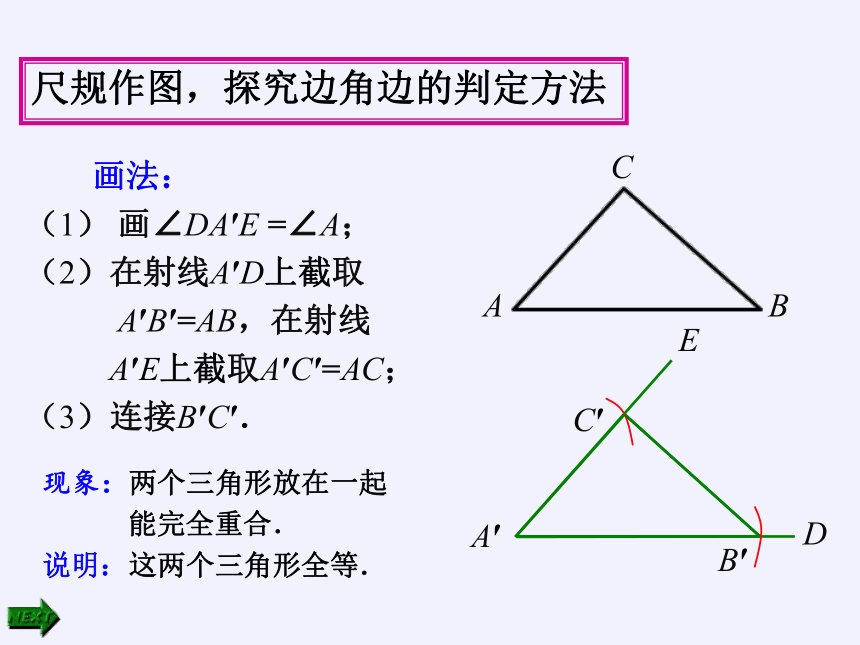
尺规作图,探究边角边的判定方法
问题1 先任意画出一个△ABC,再画一个
△A′B′C′,使A′B′=AB,∠A'=∠A,C′A′=
CA(即两边和它们的夹角分别相等).把画好的
△A′B′C′剪下来,放到△ABC 上,它们全等吗?
A
B
C
A
B
C
A′
D
E
尺规作图,探究边角边的判定方法
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1) 画∠DA′E =∠A;
(2)在射线A′D上截取
A′B′=AB,在射线
A′E上截取A′C′=AC;
(3)连接B′C′.
B′
C′
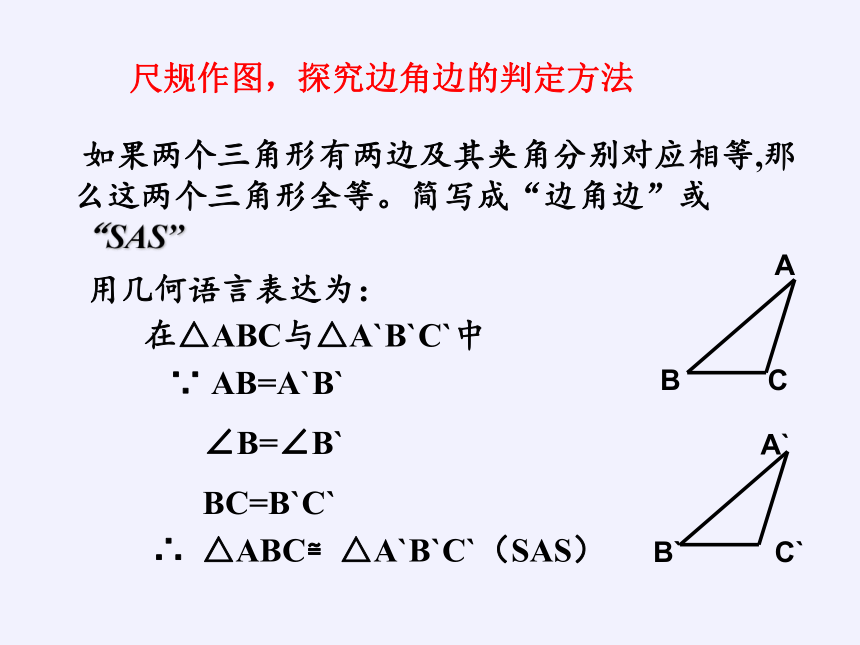
用几何语言表达为:
在△ABC与△A`B`C`中
∴ △ABC≌△A`B`C`(SAS)
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。简写成“边角边”或 “SAS”
∵ AB=A`B`
∠B=∠B`
BC=B`C`
A
B
C
A`
B`
C`
尺规作图,探究边角边的判定方法
1.在下列图中找出全等三角形,并把它们用直线连起来.
Ⅰ
?
30?
8 cm
9 cm
Ⅵ
?
30?
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅴ
30?
8 cm
?
5 cm
Ⅷ
8 cm
5 cm
?
30?
8 cm
9 cm
Ⅶ
Ⅲ
?
30?
8 cm
8 cm
Ⅲ
练习一
8 cm
Ⅱ
5 cm
30?
例1已知:如图,AD∥BC AD=BC
求证:
证明:∵AD∥BC(已知)
∴∠DAC=∠BCA(两直线平行,内错角相等)
在△ADC和△CBA中,
AD=BC(已知)
∠DAC=∠BCA(已证)
AC=CA(公共边)
∴△ADC≌△CBA(SAS)
△ADC≌△CBA
A
B
C
D
准备条件
指出范围
列举条件
得出结论
范例学习
B
C
D
E
A
例2:如图,已知AB=AC,AD=AE。
求证:∠B=∠C
C
E
A
B
A
D
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)
例3:已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
分析:
△ ABD ≌△ CBD
边:
角:
边:
AB=CB(已知)
∠ABD= ∠CBD(已知)
?
A
B
C
D
(SAS)
如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC=DF, ∠C=∠F, BC=EF;
(2) BC=BD, ∠ABC=∠ABD.
答案:
(1)全等
(2)全等
巩固练习
1、今天我们学习哪种方法可以判定两个三角形全等?
边角边(S.A.S)
2、通过这节课我们知道,当两个三角形有两边和一角对应相等时不一定全等.
到了什么?
今天你学
说一说
必做题:课本 P100 练习 1、2、3。
选做题:
小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。
布置作业
E
F
D
H
如图,在△ABC 和△ABD 中,
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
探索“SSA”能否识别两三角形全等
问题3 两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况,前面已
探索出“SAS”判定三角形全等的方法,那么由“SSA”
的条件能判定两个三角形全等吗?
A
B
C
D
谢 谢
想一想
在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。
A
B
教材97-98,一个条件可以吗?
1有一条边相等的两个三角形不一定全等
议一议
2. 有一个角相等的两个三角形
不一定全等
结论:
有一个条件相等不能保证两个三角形全等.
6cm
300
有两个条件对应相等不能保证三角形全等.
60o
300
不一定全等
有两个角对应相等的两个三角形
两个条件可以吗?
3. 有一个角和一条边对应相等的两个三角形
2. 有两条边对应相等的两个三角形
4cm
6cm
不一定全等
300
60o
4cm
6cm
不一定全等
30o
6cm
结论:
尺规作图,探究边角边的判定方法
问题1 先任意画出一个△ABC,再画一个
△A′B′C′,使A′B′=AB,∠A'=∠A,C′A′=
CA(即两边和它们的夹角分别相等).把画好的
△A′B′C′剪下来,放到△ABC 上,它们全等吗?
A
B
C
A
B
C
A′
D
E
尺规作图,探究边角边的判定方法
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1) 画∠DA′E =∠A;
(2)在射线A′D上截取
A′B′=AB,在射线
A′E上截取A′C′=AC;
(3)连接B′C′.
B′
C′
用几何语言表达为:
在△ABC与△A`B`C`中
∴ △ABC≌△A`B`C`(SAS)
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等。简写成“边角边”或 “SAS”
∵ AB=A`B`
∠B=∠B`
BC=B`C`
A
B
C
A`
B`
C`
尺规作图,探究边角边的判定方法
1.在下列图中找出全等三角形,并把它们用直线连起来.
Ⅰ
?
30?
8 cm
9 cm
Ⅵ
?
30?
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅴ
30?
8 cm
?
5 cm
Ⅷ
8 cm
5 cm
?
30?
8 cm
9 cm
Ⅶ
Ⅲ
?
30?
8 cm
8 cm
Ⅲ
练习一
8 cm
Ⅱ
5 cm
30?
例1已知:如图,AD∥BC AD=BC
求证:
证明:∵AD∥BC(已知)
∴∠DAC=∠BCA(两直线平行,内错角相等)
在△ADC和△CBA中,
AD=BC(已知)
∠DAC=∠BCA(已证)
AC=CA(公共边)
∴△ADC≌△CBA(SAS)
△ADC≌△CBA
A
B
C
D
准备条件
指出范围
列举条件
得出结论
范例学习
B
C
D
E
A
例2:如图,已知AB=AC,AD=AE。
求证:∠B=∠C
C
E
A
B
A
D
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)
例3:已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
分析:
△ ABD ≌△ CBD
边:
角:
边:
AB=CB(已知)
∠ABD= ∠CBD(已知)
?
A
B
C
D
(SAS)
如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC=DF, ∠C=∠F, BC=EF;
(2) BC=BD, ∠ABC=∠ABD.
答案:
(1)全等
(2)全等
巩固练习
1、今天我们学习哪种方法可以判定两个三角形全等?
边角边(S.A.S)
2、通过这节课我们知道,当两个三角形有两边和一角对应相等时不一定全等.
到了什么?
今天你学
说一说
必做题:课本 P100 练习 1、2、3。
选做题:
小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。
布置作业
E
F
D
H
如图,在△ABC 和△ABD 中,
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
探索“SSA”能否识别两三角形全等
问题3 两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况,前面已
探索出“SAS”判定三角形全等的方法,那么由“SSA”
的条件能判定两个三角形全等吗?
A
B
C
D
谢 谢
